LEEC - Teoria dos Circuitos Grandezas e leis fundamentais

LEEC - Teoria dos Circuitos
Grandezas e leis fundamentais - 1
Grandezas e leis fundamentais
1.
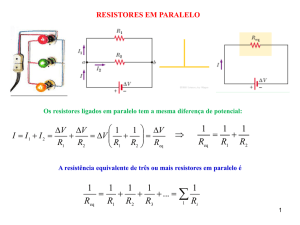
Usar as leis de Ohm e de Kirchhoff para determinar o valor da resistência R no circuito que a seguir se
apresenta. Calcular a potência absorvida por cada um dos elementos do circuito.
R
150 V
+
100 V
+
-
20 Ω
5Ω
-
2.
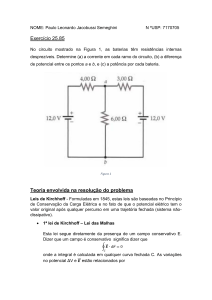
Usar as leis de Ohm e de Kirchhoff para calcular a potência absorvida por cada uma das resistências do
circuito a seguir representado.
2.5 Ω
6Ω
100 V
30 Ω
+
-
5Ω
20 Ω
3.
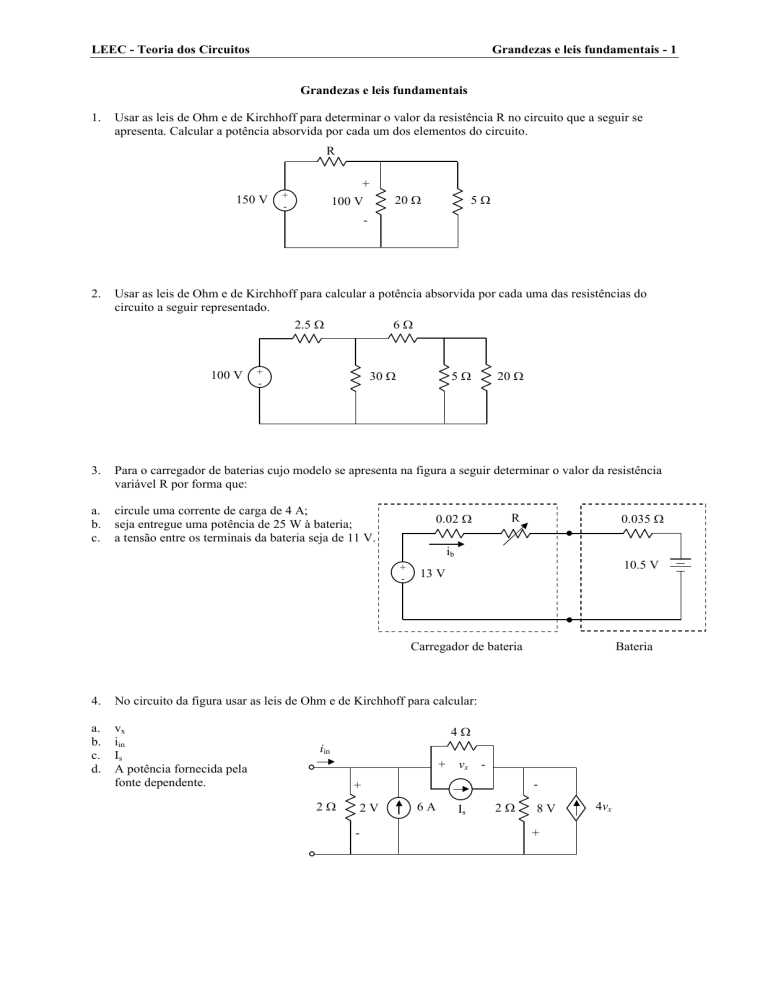
Para o carregador de baterias cujo modelo se apresenta na figura a seguir determinar o valor da resistência
variável R por forma que:
a.
b.
c.
circule uma corrente de carga de 4 A;
seja entregue uma potência de 25 W à bateria;
a tensão entre os terminais da bateria seja de 11 V.
0.02 Ω
0.035 Ω
R
ib
+
-
10.5 V
13 V
Carregador de bateria
4.
No circuito da figura usar as leis de Ohm e de Kirchhoff para calcular:
a.
b.
c.
d.
vx
iin
Is
A potência fornecida pela
fonte dependente.
Bateria
4Ω
iin
+
vx
-
+
2Ω
2V
-
6A
Is
2Ω
8V
+
4vx
LEEC - Teoria dos Circuitos
Grandezas e leis fundamentais - 2
5.
Para o circuito da figura determinar:
a.
b.
c.
Req quando R=80 Ω;
R quando Req=80 Ω;
R quando R=Req.
10 Ω
40 Ω
R
100 Ω
R eq
30 Ω
6.
No circuito da figura usar divisão de tensão e de corrente para escrever expressões para:
a.
b.
c.
v2
v1
i4
R1
+
R3
v1
-
+
R2
v2
Vs +
-
i4
R4
-
7.
Determinar as correntes i2, i1 e i0 no circuito a seguir representado.
2Ω
+
24 V
+
-
10 Ω
v∆
0.8v∆
i1
i0
20 Ω
5Ω
i2
Soluções
1.
R=2Ω
2.
p2.5 = 250 W,
3.
a. R = 0.57 Ω
4.
a. vx = 10 V
5.
a. Req = 60 Ω
6.
a.
v2 =
b.
v1 =
c.
i4 =
7.
p30 = 187.5 W,
p6 = 337.5 W,
b. R = 1.0033 Ω
b. iin = -49 A
R 2 ( R 3 +R 4 )
Vs
R 1 ( R 2 +R 3 +R 4 ) +R 2 ( R 3 +R 4 )
Vs
R2
Vs
R 1 ( R 2 +R 3 +R 4 ) +R 2 ( R 3 +R 4 )
i0 = -12.8 A,
i1 = -3.2 A,
i2 = 0 A.
d. p = -320 W
c. R = 51.8 Ω
R1 ( R 2 +R 3 +R 4 ) +R 2 ( R 3 +R 4 )
R 1 ( R 2 +R 3 +R 4 )
p20 = 45 W.
c. R = 0.12 Ω
c. Is = -46.5 A
b. R = 213.3 Ω
p5 = 180 W,
20 Ω