2ª parte

RESISTORES EM PARALELO
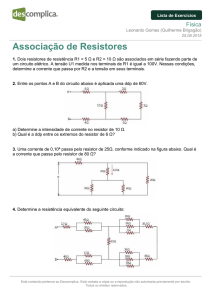
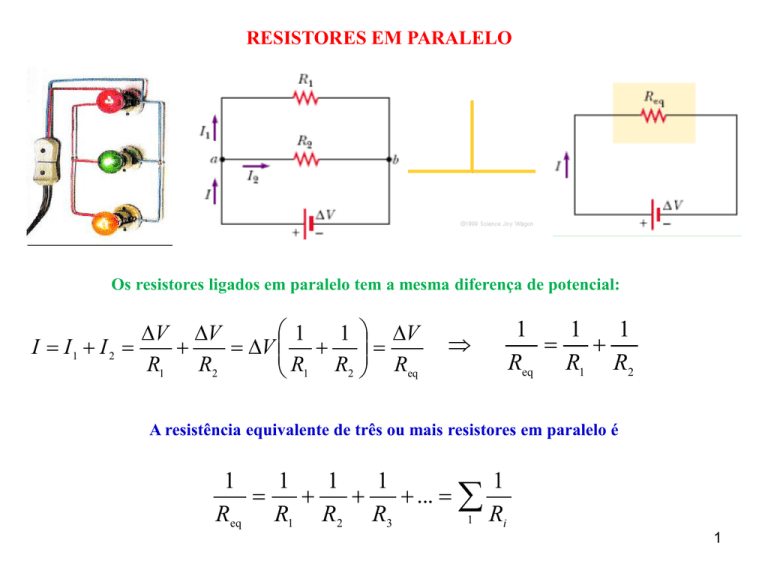
Os resistores ligados em paralelo tem a mesma diferença de potencial:
 1
V V
1  V
I  I1  I 2 

 V    
R1
R2
 R1 R2  Req

1
1
1


Req R1 R2
A resistência equivalente de três ou mais resistores em paralelo é
1
1
1
1
1



 ...  
Req R1 R2 R3
1 Ri
1
Exemplo 1
Um aquecedor de 1250 W é construído para operar sob uma tensão de 115 V.
(a) Qual será a corrente no aquecedor?
(b) Qual é a resistência da bobina de aquecimento?
(c) Que quantidade de energia térmica é gerada pelo aquecedor em 1 hora?
2
Exemplo 2
U
U
3
Exemplo 4. Calcular a resistência equivalente e a corrente que passa no circuito.
Temos: R3 em serie com R4 e com R5. Resulta em:
R6  R3  R4  R5
 (20  30  50)   100 
No circuito resultante R6 ficou em paralelo com R2:

1
1
1
1
1




 R7  60 
R7 R6 R2 100 150
R7 está em série com R1, e é a
última simplificação:
Req  R1  R7
 (30  60)   90 
A corrente que passa no circuito 
V  Req I  I 
V 18 V

 0.2 A
Req 90 
REGRAS DE KIRCHOFF
Para analisar circuitos mais completos convém utilizar duas regras simples
• A soma das correntes que entram em qualquer nó é igual à soma das correntes que saem desse
nó  regras dos nós
• A soma das diferenças de potencial em todos os elementos de uma malha fechada do circuito
é igual à zero.
5
Exemplo: Circuito de várias malhas
6
……da aula anterior, sobre condensadores (capacitores)
Carregamos o condensador ligando os dois condutores descarregados aos terminais de
uma bateria.
+
+
ΔV
+ +
+ +
+ +
Resultado final: uma carga positiva na placa h e uma carga negativa na placa l
Uma vez que isso é feito e a bateria é desconectada, as cargas permanecerão nos
condutores.
8
9
10
Nota : e
t
RC
e
RC
RC
 e 1  0.37 e (1 - e 1 )  0.63
11
12
Exemplo
13