lista resolvida de funcao exponencial - Instituto Montessori

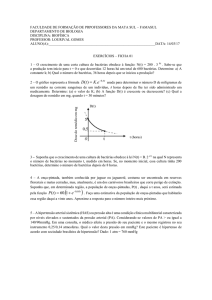
1) (UF – MT) A figura mostra um esboço do gráfico da função real de variável real
f ( x)  a x  b , com a e b reais, a > 0 e a ≠ 1. Calcule a 3  b 3 .
Solução. Observando os pontos marcados no gráfico, temos: (0, 2) e (1, 4).
 f (0)  2
 1 b  2  b  1
i) 
0
 f (0)  a  b
 f (1)  4
ii) 
 f (1)  a  1
1
 a  1  4  a  3 . O valor pedido é a 3  b 3  33  13  27  1  28 .
2) Se f(t) = 10.2t é uma função que avalia a evolução de uma cultura de bactérias, em t horas, ao cabo de quantas horas
teremos f(t) = 5120?
Solução. O exercício resume-se em igualar as informações e resolver a equação exponencial.
 f (t )  5120
 10.2 t  5120  2 t  512  2 t  2 9  t  9 . Ao fim de 9 horas.

t
 f (t )  10.2
3) O gráfico representa a fórmula D(t )  K .e 0, 4t usada para determinar o número D de miligramas de um remédio na
corrente sanguínea de um indivíduo, t horas depois de lhe ter sido administrado um medicamento ( e 0, 4  0,67 ).
a) Determine o valor de K.
b) A função D(t) é crescente ou decrescente? Justifique.
c) Quanto tempo leva para que a quantidade do medicamento administrado se reduza à metade?
Solução. Observando o gráfico vemos que se t = 0, D(t) = 5.
0, 4 ( 0 )
 5  K .(1)  K  5 .
a) D(0)  K .e
b) Decrescente. O valor em t = 0 é maior que o valor após t horas.
D(t )  2,5
c) 
D(t )  5.e
0, 4t
7
 5.e 0, 4t  2,5  e 0, 4t  0,5  4t  ln 0,5  4t  0,7  t  .horas  1h45 min
4
4) A onça-pintada, também conhecida por jaguar ou jaguaretê, costuma ser encontrada em reservas florestais e matas
cerradas, mas, atualmente, é um dos carnívoros brasileiros que corre perigo de extinção. Suponha que, em determinada

região, a população de onças-pintadas, P(t) , daqui a t anos, será estimada pela função P(t )  60. 1  e 0,05t
 . Faça uma
estimativa da população de onças-pintadas que habitarão essa região daqui a vinte anos. Aproxime a resposta para o número
inteiro mais próximo. (Utilize e = 2,7).
Solução. Basta calcular P(20). Substituindo os valores, temos:
1 e 
P(t )  60. 1  e 0, 05t  P(20)  60. 1  e 0, 05( 20)  60. 1  e 1  60.
  82
 e 






5) (Livro: Matemática - Ciência e Aplicações) Uma imobiliária acredita que o valor v de um imóvel no litoral varia segundo a
lei v(t )  60000.(0,9) t , em que t é o número de anos contados a partir de hoje.
a) Qual é o valor atual desse imóvel?
0
Solução. O valor atual é considerado em t = 0. Logo, v(0)  60000.(0,9)  R$60000,00
b) Qual é a desvalorização percentual anual desse imóvel?
Solução. Essa desvalorização será calculada entre o valor atual e o valor 1 ano depois. Ou seja, calculamos o valor
para t = 1 e comparamos com o atual.
0

60000  54000
v(0)  60000.(0,9)  R$60000,00
 Desvaloriz ação 
 0,1  0,10  10%

1
60000

v(1)  60000.(0,9)  (60000).(0,9)  54000
c) Quanto valerá esse imóvel daqui a 2 anos?
Solução. Basta calcular v(2), isto é o valor da função para t = 2.
v(2)  60000.(0,9) 2  (60000).(0,81)  R$48600,00 . Repare que poderíamos ter calculado esse valor sabendo que
estará desvalorizado em 10% em relação ao preço calculado em 1 ano. Daqui a 1 ano ele custará R$54000. A
desvalorização um ano depois será de 10% de 54000 = 5400. Logo em dois anos o imóvel custará a diferença 54000 –
5400 = R$48600,00.
d) Daqui a quantos anos o imóvel valerá R$35429,40? (Dado: 9 5  59049 )
Solução. Pede-se encontrar “t” tal que v(t) = 35429,40.
2

2 2.311.5.10 2
v(t )  35429,40  3542940  10
2 11
2
5
4
t
t

2
.
3
.
5
.
10

2
.
3
.
5
.(
0
,
9
)

(
0
,
9
)

.

5
4
t
2
.
3
.
5

v
(
t
)

60000
.(
0
,
9
)

Simplificando
os
310.10 2 310.10 2 310.10 2


termos, vem: (0,9) 
. Escrevendo os termos em frações decimais, temos:
2 3.53
2.53
103
t
 
5
t
5
310
32
9
9

    t  5 . Logo, daqui a 5 anos.
  
5
5
10 10  10 
 10 
5) Certa substância radioativa desintegra-se de modo que, decorrido o tempo t, em anos, a quantidade ainda
não desintegrada da substância é S = S0 . 2-0,25t, em que S0 representa a quantidade de substância que
havia no início. Qual é o valor de t para que a metade da quantidade inicial desintegre-se?
Solução :
𝟏
𝟐
𝒔𝟎
𝟐
= S0 . 2-0,25t
= 𝟐−𝟎,𝟐𝟓𝒕 → 𝟐−𝟏 = 2-0,25t → -0,25t = -1 → t = 4 anos
6) Suponha que o crescimento de uma cultura de bactérias obedece à lei N(t) = m. 2 t/2, na qual N representa
o número de bactérias no momento t, medido em horas. Se, no momento inicial, essa cultura tinha 200
bactérias, determine o número de bactérias depois de 8 horas.
Solução:
𝟎
𝒕
Momento inicial t = 0 e N(t) = 200, então : 200 = m . 𝟐𝟐 , logo m = 200 e a função fica N(t) = 200. 𝟐𝟐
𝟖
Para t = 8 , temos : N(8) = 200 . 𝟐𝟐 → N(8) = 200 . 2 4 → N(8) = 200 . 16 → N(t) = 3200
7) Uma população de bactérias começa com 100 e dobra a cada três horas. Assim, o número n de bactérias
após t horas é dado pela função N(t) = m. 2 t/3. Nessas condições, determine o tempo necessário para a
população ser de 51.200 bactérias.
Solução:
começa com 100 bactérias, ou seja m =100
N(t) = 100. 2 t/3
Para N(t) = 51200, temos : 51200 = 100 . 2 t/3
512 = 2 t/3
29 = 2 t/3
𝒕
9 = 𝟑 → t = 27 horas
8) A produção de uma indústria vem diminuindo ano a ano. Num certo ano, ela produziu mil
unidades de seu principal produto. A partir daí, a produção anual passou a seguir a lei y = 1000. (0,9)x. O
número de unidades produzidas no segundo ano desse período recessivo foi de:
a) 900
b) 1000
c) 180
d) 810
e) 90
Solução :
y = 1000. (0,9)2
y = 1000 . 0,81
y = 810