Solução 2 - fisicaexe.com.br

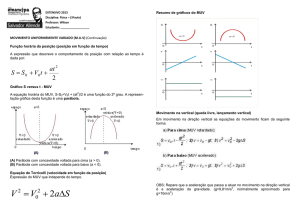
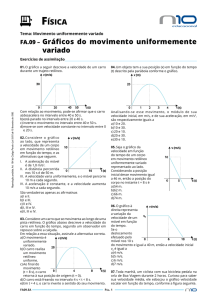
www.fisicaexe.com.br
Para um móvel em Movimento Circular Uniformemente Variado obtenha as expressões
para o cálculo da velocidade angular e do espaço angular percorrido em função do tempo
Solução
Sendo α =
dω
, com a aceleração angular α constante, no Movimento Circular
dt
Uniformemente Variado integramos esta expressão em d t de ambos os lados e obtemos
∫
d ω'
dt' =
d t'
∫αdt'
como a aceleração angular α é constate ela "sai" da integral, sendo
d ω′
d t ′ = d ω′ e os limites
dt′
de integração que vão de ω 0 , velocidade inicial, até ω( t ) , a velocidade num instante t qualquer
para d ω′ e de t 0 , instante inicial, até t, um instante qualquer para d t ′
ω (t )
t
ω0
t0
∫ d ω′ = α ∫ d t ′
ω′
ω( t )
ω0
= α .t ′
(
t
t0
ω (t ) − ω 0 = α t − t 0
(
ω ( t ) = ω 0 + α t −t 0
)
)
que é a expressão da velocidade angular para um corpo em Movimento Circular
Uniformemente Variado.
dθ
e substituindo na expressão da velocidade temos
Escrevendo ω =
dt
dθ
= ω0 + α t − t 0
dt
(
)
integrando esta expressão em d t de ambos os lados, temos
∫
na integral do lado esquerdo
d θ′
dt′ =
dt′
∫ [ω
0
(
+ α t′ − t 0
)]dt′
d θ′
d t ' = d θ′ e no lado direito da igualdade a integral da soma é a
dt'
soma das integrais, e como ω 0 , t 0 e α são constantes elas “saem” da integral, os limites de
integração vão de θ 0 , espaço inicial, até θ( t ) , o espaço num instante t qualquer para d θ ′ e de
t 0 , instante inicial, até t, um instante qualquer para d t ′
θ (t )
t
t
t
∫ d θ′ = ω ∫ d t ′ + α ∫ t d t ′ − α t ∫ d t ′
0
θ0
0
t0
t0
1
t0
www.fisicaexe.com.br
θ′
θ (t )
θ0
= ω0 t′
t
t0
t′ 2
+α
2
t
− α .t 0 t ′
t
t0
t0
 t 2 t 02 
−α t t −t
θ (t ) − θ 0 = ω 0 t − t 0 + α 
−
0
0
 2
2 


(
)
(
 t 2 t 02
θ (t ) = θ 0 + ω 0 t − t 0 + α 
−
− t 0 t + t 02
 2
2

(
)
)




 t2
t 02 
θ (t ) = θ 0 + ω 0 t − t 0 + α 
−t0 t +
 2
2 


α 2
t − 2 t 0 t + t 02
θ (t ) = θ 0 + ω 0 t − t 0 +
2
(
)
(
)
(
(
)
θ (t ) = θ 0 + ω 0 t − t 0 +
)
α
t −t0
2
(
)2
que é a expressão do espaço para um corpo em Movimento Circular Uniformemente Variado.
2