Document

L.E.
Semana 4 – Quinta Feira
CINEMÁTICA
Movimento Uniformemente Variado - MUV
Movimento Uniformemente Variado - MUV
O que é MUV:
É um movimento descrito com:
Velocidade variável.
Aceleração constante e não nula.
Δt
Δt
ΔS1
ΔS2
S
Movimento Uniformemente Variado - MUV
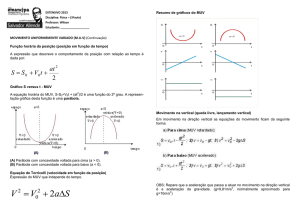
Função horária das posições (sxt):
É uma função do segundo grau que determina a posição do móvel a cada instante de movimento.
S0
s( t )
S
at
 s0  v 0  t 
2
2
S
s( t )
a 2
 s0  v 0  t   t
2
y( x )  c  b  x  a  x
2
Movimento Uniformemente Variado - MUV
Função horária das velocidades (vxt):
É uma função do primeiro grau que determina a velocidade do móvel a cada instante de movimento.
v0
v(t )  v0  a  t
v(t )  v0  a  t
y( x )  b  a  x
Movimento Uniformemente Variado - MUV
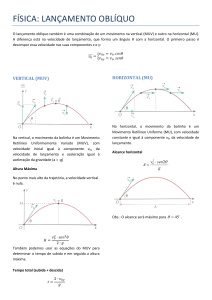
Equação de Torricelli:
É uma equação que relaciona posição velocidade e aceleração sem a necessidade do tempo.
v  v 0  2  a  s
2
2
Passar pela origem: S = 0
Mudar de sentido: v = 0
Partir da origem: S0 = 0
Partir o repouso: v0 = 0
Exercício 1
Um móvel executa um movimento cuja função horária é s = 20 – 4.t +2.t2
(SI). Determine:
a) Sua posição no instante 10 s.
s = 20 – 4.t +2.t2
s = 20 – (4.10) + 2.(10)2
s = 20 – 40 + 200
s = 180 m
Exercício 2
Um móvel executa um movimento cuja função horária é s = 20 – 4.t +2.t2 (SI).
Determine:
a/2 = 2
a = 4 m/s2
b) O instante em que muda de sentido.
Mudar de sentido: v = 0
V = V0 + a.t
0 = –4 + 4.t
4.t = 4
t=1s
Exercício 3
Um carro está se movendo com uma velocidade de 16 m/s. Em um certo instante,
o motorista avista um pedestre atravessando a rua e aciona o freio, fazendo com
que o carro adquira um movimento com aceleração de módulo 0,8 m/s2. Calcule a
velocidade desse automóvel após percorrer uma distância de 70 m a partir do
início da freada.
V0 = 16 m/s
a = – 0,8 m/s2
v  v0  2  a  s
2
2
v2  256  112
ΔS = 70 m
v  16   2   0,8  70
2
v  144
2
v  12 m / s