Relatório fis 3 exp 4

© 2013, Relatório fis 3 exp 4
EXPERIMENTO 4: ASSOCIAÇÃO DE RESISTORES
Introdução
!
Toda vez que submetemos um condutor qualquer a uma diferença de potencial
elétrico, surge entre os pólos um campo elétrico. Assim, sempre que existir uma ddp,
associada a ela existirá um campo elétrico. As linhas de campo elétrico saem das cargas
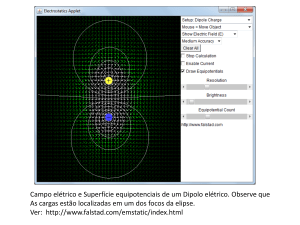
positivas e entram nas cargas negativas, como representado na figura 1:
©
!
Fig. 1 – Linhas de campo elétrico de cargas puntiformes
Se as cargas são pontuais, o vetor campo elétrico tem direção radial, saindo de uma
op
yr
ig
ht
!
carga e entrando em outra, mas se as duas são aproximadas, observemos que a linha de campo
sofre uma deformação.
!
No experimento 1 vimos que a dependência da diferença de potencial elétrica com a
distância é dada pela equação V =
K ⋅q
. Nesta equação, a diferença de potencial elétrico tem
r
um comportamento hiperbólico com a distância r. Para o caso específico da figura 1 podemos
entender a distância r, como sendo o raio de uma circunferência que envolve a carga positiva
ou negativa. Sobre este ponto de vista podemos entender que para uma circunferência de raio
r, escrita em torno da carga (positiva ou negativa), teremos sempre uma diferença de potencial
V(r) constante para o mesmo raio r. Isto nos leva a crer que existirá n linhas de n raios de
C
mesmo potencial em torno da carga chamadas linhas equipotenciais.
!
Vamos analisar as cargas da figura 1, para cada r podemos traçar uma linha
equipotencial, ou seja, uma circunferência de raio r, desta forma as linhas de campo elétrico
serão sempre perpendiculares às linhas equipotenciais. Se isto é verdade para o caso das
cargas (positivas ou negativas) colocadas separadamente, também deverá ser verdade para as
cargas colocadas uma próxima à outra. A diferença agora reside no fato de que, se as cargas
são colocadas próximas, o campo elétrico entre elas sofrerá interferência, e as linhas do vetor
E, não representam mais o raio de uma circunferência. Sendo assim, ocorre uma deformação
das linhas de campo elétrico (E) e das linhas equipotenciais.
!
Se ao invés de colocarmos duas cargas pontuais próximas, colocarmos duas placas
paralelas polarizadas, uma ficará carregada negativamente e outra ficará carregada
positivamente. Desta maneira o vetor campo elétrico sairá da placa positiva e entrará na placa
Escola de Engenharia de Lorena • USP
All rights reserved
2
© 2013, Relatório fis 3 exp 4
negativa. Este campo será bastante homogêneo na região central entre as placas, e perderá
homogeneidade nas extremidades, conforme representado na figura 1. Como as linhas
equipotenciais são perpendiculares ao campo elétrico, teremos sempre uma linha de mesmo
potencial elétrico, para cada distância d definida a partir de uma delas, tomada como
referência.
!
Como o campo elétrico é dado pela expressão E =
K ⋅q
K ⋅q
(2) e ΔV =
(3) ,
2
r
r
dividindo a expressão 2 pela 3 teremos:
ΔV = E ⋅ d , ou ainda Va = Vb + E ⋅ d (4)
!
Esta última equação pode ser traduzida graficamente como a equação de uma reta de
©
Va em função da distância d, onde E representa o coeficiente angular desta reta e Vb o seu
coeficiente linear. Se a placa de referência for negativa, o potencial V em função de d vai
aumentando, pois estamos caminhando em direção à placa positiva, desta forma a inclinação
op
yr
ig
ht
será positiva. Entretanto se a placa de referência for positiva, V irá diminuindo em função de d
e a inclinação será negativa. Esta observação permite dizer que a equação 4 admite os dois
sinais, sendo assim ela poder ser escrita de maneira genérica da seguinte forma:
Va = Vb ± E ⋅ d (5)
Objetivos
!
Visualizar as linhas equipotenciais e do campo elétrico através da medição de
potencial elétrico em uma cuba eletrolítica.
C
Procedimento Experimental
!
Encheu-se uma cuba de acrílico com água (Fig. 2).
Fig. 2 – Cuba de acrílico com H2O
!
Colocaram-se os terminais de cobre cilíndrico na cuba e ligou-os à fonte de tensão
(+3V). Colocou-se um dos terminais cilíndricos do multímetro em um dos terminais de cobre
e o outro na cuba procurando por pontos de mesmo potencial elétrico (equipotenciais). No
segundo experimento, mediu-se o potencial em função da distância para os terminais na
forma de barra retangular (Fig 3).
Escola de Engenharia de Lorena • USP
All rights reserved
3
© 2013, Relatório fis 3 exp 4
!
Fig. 3 – Barras retangulares na cuba
Resultados e discussão
Obtiveram-se experimentalmente os seguintes dados:
1,75
7,0
ΔV (V)
d (cm)
1,25
9,0
1,47
10,0
1,60
11,0
1,75
12,0
1,89
13,0
2,04
14,0
2,20
15,0
©
d (cm)
op
yr
ig
ht
ΔV (V)
1,45
8,0
1,72
9,5
2,12
11,0
Tabela 1 – Cilindro
Tabela 2 – Barras retangulares
C
A tensão utilizada na fonte foi de 3V.
Os dados obtidos foram então linearizados e comparados com a equação:
y = b ⋅x + a
↓
↓ ↓
ΔV = E ⋅ d
Foram encontrados os seguintes valores:
a = −0,02 ± 0,0212
b = 0,1475 ± 0,00174
CORR = 0,99965
Como os cálculos foram efetuados com a unidade de “d” em cm: B = E = 14, 75V
Escola de Engenharia de Lorena • USP
All rights reserved
4
© 2013, Relatório fis 3 exp 4
op
yr
ig
ht
©
!
Grafico 1 – gráfico da linearização da função V x d
!
Os resultados mostram que o experimento teve boa precisão, pois o valor do CORR
(Coeficiente de correlação) apresentou 3 noves, mostrando que o experimento foi bem
realizado, com poucos erros aleatórios.
Cálculo do erro percentual:
E exp − E teórico
E exp
⋅100% =
C
E=
!
14, 75 − 18, 75
⋅100% = 27,12%
14, 75
Esse valor indica baixa exatidão do experimento devido aos erros erros sistemáticos,
como, por exemplo, fios oxidados, mal contatos nas conexões.
Conclusão
!
De acordo com o experimento, concluí-se que é possível visualizar as linhas
equipotenciais medindo a ddp no sistema, buscando os pontos no qual tem o mesmo valor da
ddp. Finalmente, encontrando o valor do campo magnético nesse experimento, que foi dentro
do resultado esperado.
Referência Bibliográfica: Fundamentos da Física 3 – Halliday Resnick Wolker – 6ª edição –
LTC editora
Escola de Engenharia de Lorena • USP
All rights reserved
5