Campo Elétrico - WordPress.com

FATECSP - 2012
Campo Elétrico
1. Campo Elétrico
Podemos mapear a temperatura ao redor de um forno
utilizando-se de um termômetro para obter uma
distribuição de temperaturas conhecido como campo de
temperatura do forno.
Da mesma forma o campo elétrico em torno de uma
carga elétrica puntiforme q pode ser avaliado mapeando-se
ao seu redor a partir de uma carga-teste positiva, qo>0. A
carga teste sofrerá a atuação de uma força F, segundo a
lei de Coulomb.
1 qqo
Fe =
4πε o r 2
Podemos afirmar que o modelo de campo elétrico,
proposto por Faraday, é um agente intermediador das
interações entre as cargas elétricas.
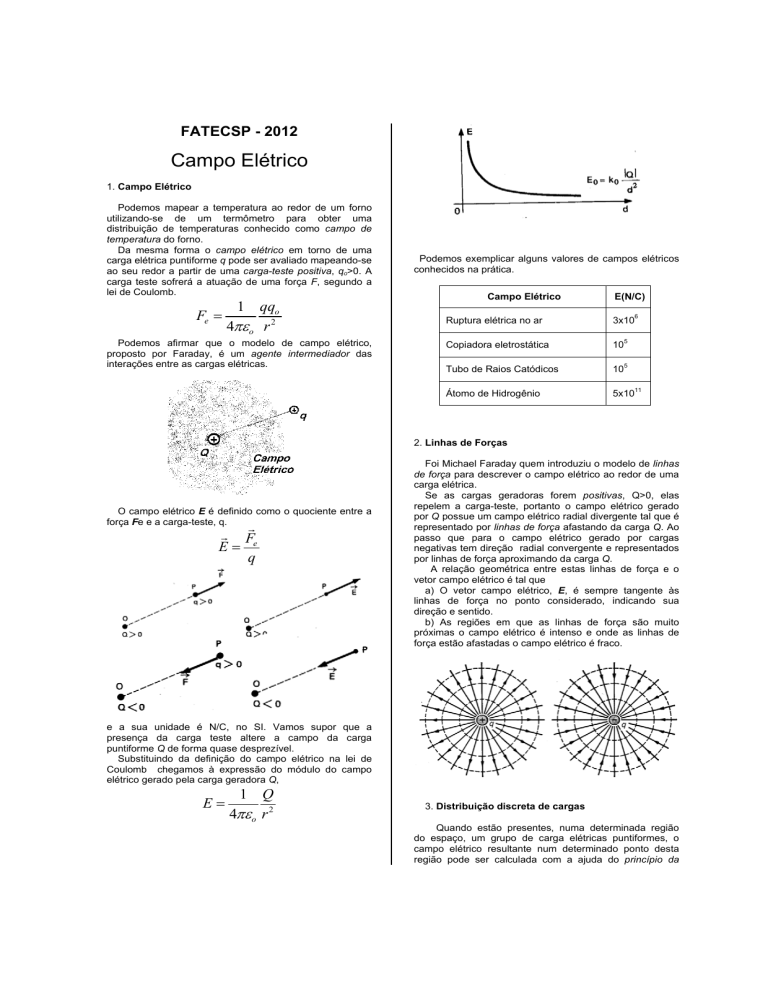
Podemos exemplicar alguns valores de campos elétricos
conhecidos na prática.
Campo Elétrico
E(N/C)
Ruptura elétrica no ar
3x10
Copiadora eletrostática
10
5
Tubo de Raios Catódicos
10
5
Átomo de Hidrogênio
5x10
6
11
2. Linhas de Forças
O campo elétrico E é definido como o quociente entre a
força Fe e a carga-teste, q.
r
r Fe
E=
q
Foi Michael Faraday quem introduziu o modelo de linhas
de força para descrever o campo elétrico ao redor de uma
carga elétrica.
Se as cargas geradoras forem positivas, Q>0, elas
repelem a carga-teste, portanto o campo elétrico gerado
por Q possue um campo elétrico radial divergente tal que é
representado por linhas de força afastando da carga Q. Ao
passo que para o campo elétrico gerado por cargas
negativas tem direção radial convergente e representados
por linhas de força aproximando da carga Q.
A relação geométrica entre estas linhas de força e o
vetor campo elétrico é tal que
a) O vetor campo elétrico, E, é sempre tangente às
linhas de força no ponto considerado, indicando sua
direção e sentido.
b) As regiões em que as linhas de força são muito
próximas o campo elétrico é intenso e onde as linhas de
força estão afastadas o campo elétrico é fraco.
e a sua unidade é N/C, no SI. Vamos supor que a
presença da carga teste altere a campo da carga
puntiforme Q de forma quase desprezível.
Substituindo da definição do campo elétrico na lei de
Coulomb chegamos à expressão do módulo do campo
elétrico gerado pela carga geradora Q,
E=
1 Q
4πε o r 2
3. Distribuição discreta de cargas
Quando estão presentes, numa determinada região
do espaço, um grupo de carga elétricas puntiformes, o
campo elétrico resultante num determinado ponto desta
região pode ser calculada com a ajuda do princípio da
superposição. Cada carga elétrica gera seu próprio campo
elétrico, naquele ponto específico, de forma independente
das outras cargas elétricas. E o campo elétrico resultante é
obtido pela soma vetorial dos campos elétricos
componentes.
Vamos calcular o campo elétrico resultante a uma
distãncia z a partir do ponto médio do dipolo cujo
espaçamento entre as cargas elétricas é d.
E=

q 
1
1


−
2
2 
4πε o  ( z − d / 2) ( z + d / 2) 
que com um pouco de álgebra chegamos a
E=
−2
−2
q  
d 
d  

1 −  − 1 +  

4πε o   2 z 
 2 z  
que para distâncias grandes z‫ب‬d podemos expandir a
expressão anterior através do binômio de Newton
r r r
r
E = E1 + E2 + E3
(1 + x )n ≈ 1 + nx
E=
q  d
  d

 1 + + .. − 1 − + .. 
4πε o  
z
  z

onde desprezando-se termos de ordem superiores ao
-2
O(z ) pois d/z‫ا‬1.
E=
q 2d
1 qd
=
3
4πε o z
2πε o z 3
O produto pd é chamado de Momento de Dipolo
Elétrico p que é um vetor orientado da carga negativa –q
para a carga positiva +q. O campo elétrico de um dipolo
elétrico p em termo de r fica
E=
Lista 2 > 5
1
p
2πεo r 3
cujo módulo decresce muito mais rapidamente do que o
campo de uma única carga puntifome pelo fato que a
longas distâncias existe um cancelamento dos campos do
dipolo porque a distãncia d do dipolo torna-se desprezível.
Vamos considerar a partir de agora campos elétricos
gerados por distribuições contínuas por cargas como, em
distribuições lineares, superficiais ou volumétricas. Nestas
distribuições usaremos os princípios de cálculo diferencial
e integral em problemas simétricos para calcular os
campos elétricos resultantes.
É admitido que os elementos diferenciais possuam
comprimento, área e volume contendo uma quantidade
razoável de cargas elétricas e serem admitidos como
cargas puntiformes, do contrário não teriam sentido físico.
Então
dimensionalmente
estes
elementos
são
macroscópicos o suficiente para conter um ‘punhado’ de
cargas elétricas mas serão microscópicos ou diferenciais
para poderem ser tratados através do cálculo.
5 Fio finito
Vamos calcular o campo elétrico gerado por um fio finito,
de comprimento
carga λ.
4 Dipolo Elétrico
Nos materiais dielétricos os elétrons estão fortemente
ligados aos átomos que sob indução de campos elétricos
externos as cargas elétricas dos átomos ficam
ligeiramente polarizados com suas cargas deslocadas em
forma de dipolos elétricos.
l,
carregado com densidade linear de
lista 2 > 9
6. Fio Infinito
Se o fio é infinito temos que para
∴ Ey =
O elemento dx contribui com
dE =
λdx
1
1
λ
l→∞
2πε o y
4πε o y 2 + x 2
que é projetado na direção de y
cosθ =
(y
y
2
+ x2
)
1/ 2
que por questões de simetria as componentes
perpendiculares são canceladas duas a duas pelo
espelhamente entre os elementos diferenciais. Somente as
componentes paralelas são adicionadas para compor o
campo elétrico resultantes na direção y.
Então
dE y = dE cosθ =
E = ∫ dE y = ∫ dE cosθ
1
(
4πε o y + x
=
7 Anel carregado com densidade linear de carga λ.
yλdx
2
yλ
4πε o
)
2 3/ 2
l/2
∫ (y
−l / 2
dx
2
+ x2
)
3/ 2
vamos resolver a integral acima substituindo a expressão,
2
x = y.tgθ , como sua diferencial
dx = y sec θ dθ
=
φ
sec2 θ
dθ
3 ∫
4πε o y −φ 1 + tgθ 2
y2
(
)
φ
Ey =
λ
cosθ ⋅ dθ =
4πε o y −∫φ
φ
Ey =
=
λ
4πεy
λ
cosθ ⋅ dθ =
4πε o y −∫φ
{sen φ − sen(− φ )} =
=
λ
sen φ
2πε o y
pela trigonometia obtemos que o ângulo φ pode ser escrito
como
sen φ =
tal que
∴ Ey =
em termos de carga,
l
l2 + 4y2
l
λ
2πε o y l 2 + 4 y 2
q = λl , obtemos
∴ Ey =
1
q
2πε o y l 2 + 4 y 2
tanθ = R / z
cosθ =
(R
⇒ R = z tan θ
z
2
+ z2 )
1/ 2
dq = λdl = λRdθ ,
O elemento diferencial de carga,
substituido na expressão do campo elétrico fica
dE =
λR
1 dq
dθ
=
4πε o a 2 4πε o R 2 + z 2
(
)
que por questões de simetria as componentes
diametralmente opostos são cancelados dois a dois entre
os elementos diferenciais do anel. É somente as
componentes paralelas são adicionadas para compor o
campo elétrico resultantes na direção z.
 λR
dθ 
z
dE z = dE cosθ = 
2
2 
2
πε
4
R
z
+
o

 R + z2
(
)(
)
1/ 2
=
λRz
dθ
4πε o R 2 + z 2
(
)
E=
3/ 2
E = ∫ dE z = ∫ dE cos θ
=
2π
λ
Rz
dθ
4πε o (R 2 + z 2 )3 / 2 ∫0
Rz
λ
2ε o (R 2 + z 2 )3 / 2
∴ Ey =
zσ
4ε o
dy
∫y
3/ 2
1
− zσ 
=

2ε o  r 2 + z 2
(
=
zσ
4ε o
∫y
−3
R
)
1/ 2

zσ
+ cte =
2
ε0
 0
∴E =
σ
2ε o

zσ  1
+ cte =

4ε o  y

dy = (− 2)
1
1
 − 2
z
R + z2


z
1 − 2
R + z2

(
(
)
1/ 2
)
1/ 2






Agora, em termos da carga q chegamos a
∴E =


σπR 2 
z
q 
z
=
1−
1−
2 
1/ 2 
2 
1/ 2 
2
2
2
2
2πε o R  (R + z )  2πε o R  (R + z ) 
Lista 2 > 10
8. Disco carregado
Vamos fazer uso da expressão final do campo elétrico
azimutal de anel do item 7 anteiror em termos da carga q
utilizamos q = λ2πR, na forma .
Ey =
q
(
z
4πε o R + z 2
2
)
Obs : o campo elétrico próximo à superfície da Terra é
aproximadamente 150 N/C descendente.
Lista 2 > 11
8. Plano Infinito
3/ 2
Para p cálculo de campo elétrico gerado por um plano
infinito temos duas alternativas calculando o campo
elétrico muito próximo do plano carregado, z<<R , ou
tomando R para o infinito..
com densidade superficial σ de carga.
E=
σ 
z
1 − 2
2ε o 
R + z2
(
)
1/ 2
 σ
=
 2ε o
 z
1 − R 
como o termo z/R é desprezível, então
∴E =
σ
2ε o
A carga elétrica contida no elemento anular de raio r e
espessura dr que contém um densidade superficial σ, é
dado por dq = σ(2πρdr).
O campo elétrico do elemento anular diferencial na
posição z é dado por
dE =
z
dq
4πε o r 2 + z 2
(
)
3/ 2
=
zσ 2π
rdr
4πε o r 2 + z 2
(
)
3/ 2
então integrando-o de 0 a R, temos que
E = ∫ dE =
Substituindo
zσ
2ε o
R
∫ (r
0
rdr
2
+ z2
)
3/ 2
y = z 2 + r 2 e dy = 2rdr temos
Representa o campo elétrico de um plano infinito !!!
9. Aproximações para cargas puntiformes
O cálculo do campo elétrico num ponto muito distante, z
>>R
E=
σ
2ε o
e como

z
1 −
 z 1 + R 2 / z 2
(
(R / z )
de Newton,
E=
2
 σ   R 2  −1 / 2 
1 − 1 + 2  
=
1/ 2 
z  
 2ε o  

)
<<1 podemos aproximar com o binômio
(1 + x )n ≈ 1 + nx , e termos
σ   R 2  σ
 =
1 − 1 −
2ε o   2 z 2  2ε o
∴E =

R 2  σR 2 π
1 − 1 + 2  =
2 z  4ε o z 2 π

1
q
4πε o z 2
Então para grandes distâncias d, o campo elétrico
produzido pela distribuição de cargas produz um um
campo elétrico comportando-se como uma carga
puntiforme.
10. Materiais Condutores
Nenhum excesso de carga será encontrado no interior
de um material condutor.
Eint = 0
Os elétrons de condução redistribuem-se e o excesso
de carga migra para a superfície do condutor.
O campo elétrico surge apenas no início da redistribuição
e logo se anula, estabelecendo um equilíbrio eletrostático.