Falhas

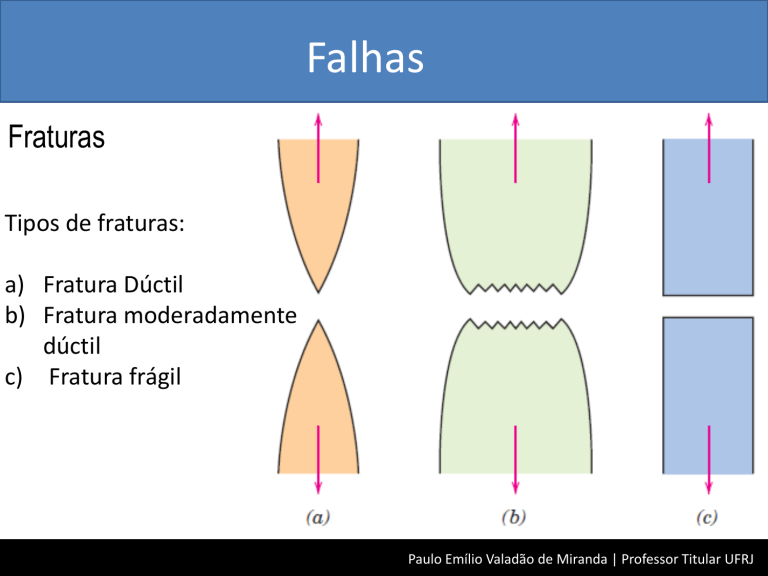
Falhas
Fraturas
Tipos de fraturas:
a) Fratura Dúctil
b) Fratura moderadamente
dúctil
c) Fratura frágil
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Estágios da fratura dúctil,
tipo taça e cone:
a) Empescoçamento inicial
b) Formação de cavidades
c) Coalescência de
cavidades para formar
trinca
d) Propagação da trinca
e) Fratura por cisalhamento
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Fratura dúctil
Micro vazios
associados à
fratura dúctil,
revelados por
Microscopia
Eletrônica de
Varredura
Fratura tipo taça e cone
no alumínio
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Fratura dúctil
Fractografia eletrônica por varredura
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Fratura frágil
em aço doce
Marcas de
sargento em
forma de V
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Fratura frágil
Nervuras radiais em formato de leque
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Grãos
Caminho de
propagação
da trinca
Morfologia de fratura
transgranular ou
transcristalina em ferro
fundido dúctil
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Grãos
Caminho de
propagação
da trinca
Morfologia de fratura
intergranular ou
intercristalina
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Trincas: concentração de
tensões
a) Geometria de trincas superficiais
e internas
b) Perfil de tensões esquemático ao
longo da linha X – X’
Tensão
máxima
= Tensão
trativa nominal
Fator de intensidade
de tensão
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Trincas
Onde:
σm
= Tensão máxima, na extremidade da
trinca
σ0 = Tensão de tração nominal
σc = Tensão crítica
E = Módulo de elasticidade
γs = Energia de superfície específica
a = Comprimento de uma trinca superficial metade do comprimento de uma trinca
interna
ρ0 = Raio da extremidade da trinca
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Mecânica da Fratura
Linear Elástica
Onde
Kc=Tenacidade à fratura
KIc=Tenacidade à fratura em deformação plana
Y=Parâmetro que depende da geometria e do tamanha da trinca e das tensões.
σc=Tensão crítica
a=Comprimento de uma trinca superficial/metade do comprimento de uma trinca
interna
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Modos de Deslocamento
de trincas
I
II
III
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas: Ensaios de Fratura por Impacto
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Transição
dúctil-frágil
Morfologias de fratura de
Aço A36 testados em
Charpy com entalhe em V
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Transição
dúctilfrágil
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Transição
dúctilfrágil
Efeito do
teor de
carbono
no aço
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas: Fadiga
= -1
Ciclos de tensão
a) reverso simétrico;
b) assimétrico e
c) aleatório
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Fadiga
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Fadiga de Componentes Reais
1 – Hydraulic Actuator
2 – End Support Assembly
3 – Transverse Load Frame
4 – Connector
5 – Shaft
6 – Specimen
7 – Grips
8 – Driving Mechanism
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Fadiga
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falhas
Fadiga
P = probabilidade
de falha
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falha por Fadiga
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Fadiga
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Falha por Fadiga
600MPa
600X
Drill pipe
API S –135
grade steel
25X
500X
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Fadiga em Liga de Al
50X
400
S - N diagram for D16T alloy
small scale results
full scale results
350
300
σa(MPa)
250
200
150
100
50
0
103
104
105
106
107
Number of Cylces
33X
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Nucleação e Crescimento
de Bandas de Deslizamento
Ao longo dos ciclos cresce o número e a densidade de bandas e a
deformação plástica acumulada em cada uma delas;
Nos locais de deformação plástica mais severa as bandas de deslizamento
recebem a denominação de bandas de deslizamento persistentes.
τ = σ cos φ cos λ
Fator de Schmid. A tensão cisalhante é resolvida no sistema de deslizamento.
Bandas de Deslizamento
Essa deformação plástica
é
extermamente
localizada e se manifesta
na forma de bandas de
deslizamento;
A
concentração
de
tensão cresce com o
aumento do número de
bandas de deslizamento
fazendo com que o
material acumule cada
vez mais deformação
plástica, surgindo novas
bandas de deslizamento.
Bandas de Deslizamento
Bandas de Deslizamento
Bandas de Deslizamento
e
d
a
b
c
Intrusões e Extrusões
Um conjunto de bandas formam intrusões e
extrusões na superfície do material.
Bandas de Deslizamento Persistentes
Iniciação de Trincas (estágio I)
Em orientações cristalinas
com fator de schmid elevado,
a deformação plástica é mais
severa, sendo as bandas de
deslizamento desses grãos
chamadas de bandas de
deslizamento persistentes;
Nas bandas de deslizamento
persistentes a concentração
de tensões é mais intensa;
Quando o material não é mais
capaz
de
acumular
deformação
plástica
nas
bandas
de
deslizamento
persistentes uma ou mais
trincas são nucleadas.
Propagação de Trincas (estágio II)
Com o crescente número de ciclos a(s) trinca(s)
se propagam de maneira dúctil crescendo
enquanto na componente trativa, e fechando a
ponta da trinca na componente compressiva
Marcas de Praia
A propagação da
trinca forma relevos
característicos
da
fadiga, são chamados
de marcas de praia
(macroscópicas)
e
estrias
de
fadiga
(microscópicas)
Estrias de Fadiga
Ruptura Final Estática
Ao
atingir
um
determinado tamanho
a seção resistente
remanescente
do
material não suporta
mais
a
tensão
aplicada. O material
sofre então ruptura
final
estática
por
sobretensão
Fluência
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Fluência
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Fluência
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Fluência
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Fluência
Parâmetro de
Larson-Miller
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ
Fluência
Paulo Emílio Valadão de Miranda | Professor Titular UFRJ