Lista final de exercicios

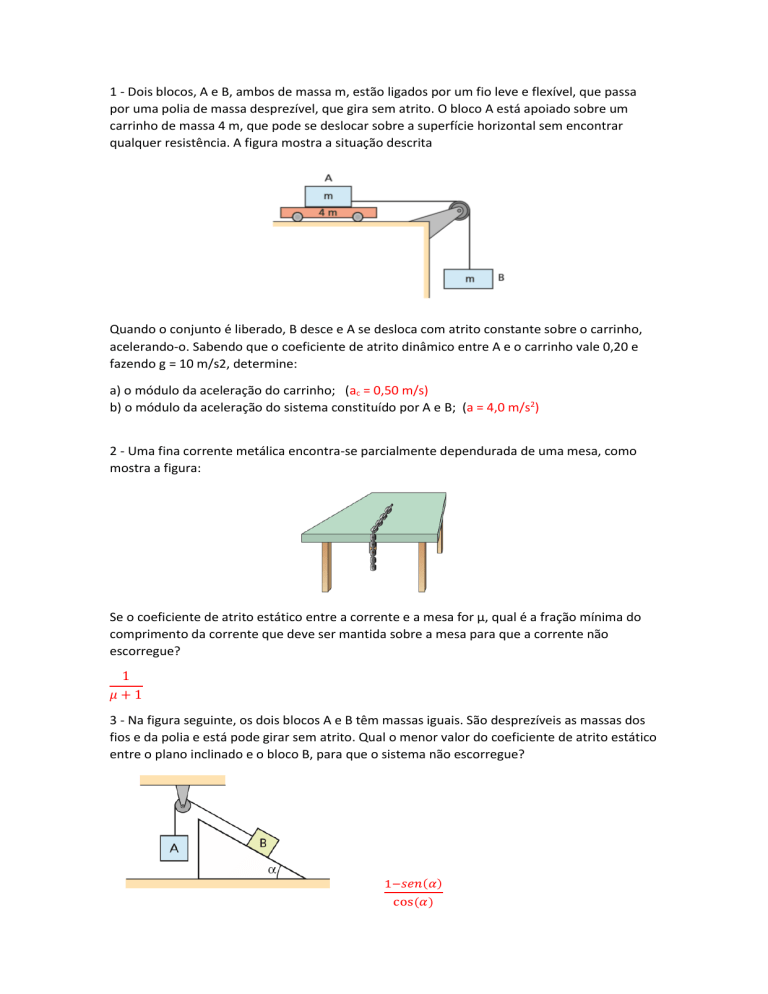
1 - Dois blocos, A e B, ambos de massa m, estão ligados por um fio leve e flexível, que passa
por uma polia de massa desprezível, que gira sem atrito. O bloco A está apoiado sobre um
carrinho de massa 4 m, que pode se deslocar sobre a superfície horizontal sem encontrar
qualquer resistência. A figura mostra a situação descrita
Quando o conjunto é liberado, B desce e A se desloca com atrito constante sobre o carrinho,
acelerando-o. Sabendo que o coeficiente de atrito dinâmico entre A e o carrinho vale 0,20 e
fazendo g = 10 m/s2, determine:
a) o módulo da aceleração do carrinho; (ac = 0,50 m/s)
b) o módulo da aceleração do sistema constituído por A e B; (a = 4,0 m/s2)
2 - Uma fina corrente metálica encontra-se parcialmente dependurada de uma mesa, como
mostra a figura:
Se o coeficiente de atrito estático entre a corrente e a mesa for μ, qual é a fração mínima do
comprimento da corrente que deve ser mantida sobre a mesa para que a corrente não
escorregue?
1
𝜇+1
3 - Na figura seguinte, os dois blocos A e B têm massas iguais. São desprezíveis as massas dos
fios e da polia e está pode girar sem atrito. Qual o menor valor do coeficiente de atrito estático
entre o plano inclinado e o bloco B, para que o sistema não escorregue?
1−𝑠𝑒𝑛(𝛼)
cos⁡(𝛼)
4 - Na figura, os blocos A e B são iguais, apresentando peso de intensidade igual a 100 N cada
um. Os coeficientes de atrito estático entre A e B e entre B e a superfície do plano inclinado
têm o mesmo valor: μ. Dados: sem (θ) = 0,60; cos(θ) = 0,80.
Sabendo que os blocos estão em equilíbrio, com B na iminência de escorregar, calcule:
a) o valor de μ; (µ = 0,25)
b) a intensidade da força de tração no fio. (T = 80 N)
5- A figura abaixo representa três blocos de massas M1 = 1,00 kg, M2 = 2,50 kg e M3 = 0,50 kg
respectivamente. Entre os blocos e o piso que os apoia existe atrito, cujos coeficientes cinético
e estático são, respectivamente, 0,10 e 0,15; a aceleração da gravidade vale 10,0 m/s2.
Se ao bloco 1 for aplicada uma força F horizontal de 10,0 N, qual será a intensidade da força
que o bloco 2 exercerá no bloco 3? (F = 1,25 N)
6 - A figura abaixo mostra, em um plano vertical, parte dos trilhos do percurso de uma
montanha russa de um parque de diversões. Qual a velocidade mínima que o carrinho deve
ter, ao passar pelo ponto mais alto da trajetória, para não desgrudar dos trilhos? 6m/s
7 - Um carro que pesa 1000kg faz uma curva cujo raio é de 2 metros. Sabendo que o
coeficiente de atrito estático do pneu do carro com o asfalto é de 0,8, qual a maior velocidade
para o carro fazer a curva sem derrapar? 4m/s
8-
Sabendo que um ciclista pedala com velocidade constante de tal forma que o pedal dá duas
voltas em um segundo. Qual a velocidade linear, em km/h da bicicleta? 15,072 m/s
9 - Um carro cuja roda tem 30 cm de raio está em uma pista circular de raio igual a 18 metros.
A velocidade do carro é constante e tal que, a roda dele gira 10 vezes por segundo. Considere
π = 3.
a) Qual a velocidade do carro, em km/h? 64,8km/h
b) Qual a aceleração do carro para que ele faça a trajetória circular da pista sem sair dela?
18m/s2
c) Quanto tempo, em minutos, o carro leva para dar 25 voltas na pista? 2,5 minutos
10 - Na rampa de saída do supermercado, uma pessoa abandona, no instante t= 0, um
carrinho de compras de massa 5 kg que adquire uma aceleração constante. Considere cada um
dos três primeiros intervalos de tempo do movimento iguais a 1 s. No primeiro e no segundo
intervalos de tempo, o carrinho percorre, respectivamente, as distâncias de 0,5 m e 1,5 m.
Calcule:
a) o momento linear que o carrinho adquire no instante t=3 s; 15kgm/s
b) a distância percorrida pelo carrinho no terceiro intervalo de tempo. 2,5m
11 - Durante a madrugada, um carro de luxo, de massa total igual a 2400 kg bate na traseira de
um carro de massa igual a 1200 kg, que estava parado no sinal vermelho. O motorista do carro
de luxo alega que o outro estava com as luzes apagadas, e que ele vinha reduzindo a marcha
ao aproximar-se do sinal, e que estava a menos de 10km/h quando o acidente aconteceu. A
perícia constata que o carro de luxo arrastou o outro de uma distância igual a 10,5 metros e
estima que o coeficiente de atrito cinético com a estrada no local do acidente é de 0,6. Qual
era a real velocidade do carro de luxo? 60km/h.
12 - Uma bala de 5g incide sobre um pêndulo balístico de massa igual a 2kg, com uma
velocidade de 400m/s, atravessando a massa, emergindo do outro lado com velocidade de
100m/s. Qual a velocidade do pendulo após a bala sair? 0,75m/s
13 - A modificação rápida do movimento do corpo é a característica principal da maioria dos
esportes e dos brinquedos nos parques de diversão. Essa modificação do movimento é
responsável pela sensação de prazer causada por esses “jogos do corpo”, a qual os
bioquímicos associam à produção de adrenalina.
Em um parque de diversões, uma jovem de 40kg brinca em uma cama elástica, representada
na figura. Ela pula de uma altura h =1,8m e, durante 0,5 segundo, a cama freia o movimento da
jovem até pará-la, empurrando-a, posteriormente, para cima. Sabendo que, ao atingir a cama,
o movimento da jovem é na direção vertical, calcule a força elástica média que a cama exerce
sobre ela até pará-la. Considere a aceleração da gravidade como sendo 10m/s2. 880 N
14 - Um menino de 40kg está sobre um skate que se move com velocidade constante de
3,0m/s numa trajetória retilínea e horizontal. Defronte de um obstáculo ele salta e após 1,0s
cai sobre o skate que durante todo tempo mantém a velocidade de 3,0m/s
Desprezando-se eventuais forças de atrito, pede-se:
a) a altura que o menino atingiu no seu salto, tomando como referência a base do skate.
b) a quantidade de movimento do menino no ponto mais alto de sua trajetória.
a) h = 1,25 m b) Q = 120 kg.m/s
15 – Por engano, as rodas da direita de um automóvel foram trocadas por rodas menores, de
25 cm de raio. As rodas da esquerda de 30 cm de raio não foram trocadas. Quando o motorista
tentava segurar o volante na posição em que o carro deveria andar em linha reta, o carro fazia
uma trajetória circular. Sabendo que a distância entre as rodas da esquerda e da direita, tanto
na frente quanto atrás, é de 1,5 metros, e que as rodas apresentem o tempo todo a mesma
velocidade angular, calcule o raio desta trajetória circular. Tome como referência a trajetória
que a roda da esquerda faz. 9 metros
16 – Por engano, as todas de um carro, que eram de 60 cm de diâmetro, foram trocadas por
outra, de 50 cm de diâmetro. Nesta condição, quando o velocímetro marca 90km/h, qual a real
velocidade do automóvel? 75km/h.
17- Há alguns anos, noticiou-se que um avião foi obrigado a fazer um pouso de emergência
em virtude de uma trinca no para-brisas causada pela colisão com uma pedra de gelo.
Leve em conta as hipóteses abaixo:
1 - A aeronave se deslocava horizontalmente à velocidade de 200 m/s, não havendo alteração
nesta velocidade após a colisão.
2 - Massa da pedra de gelo 25 gramas e velocidade desprezível
3 - O para-brisas do avião considerado vertical
4 - O intervalo de tempo de colisão igual a 0,002 s.
Com estas hipóteses, qual foi a força média de colisão? 2500N