Lista Complementar de Física

Lista Complementar de Física – Prof. Roni
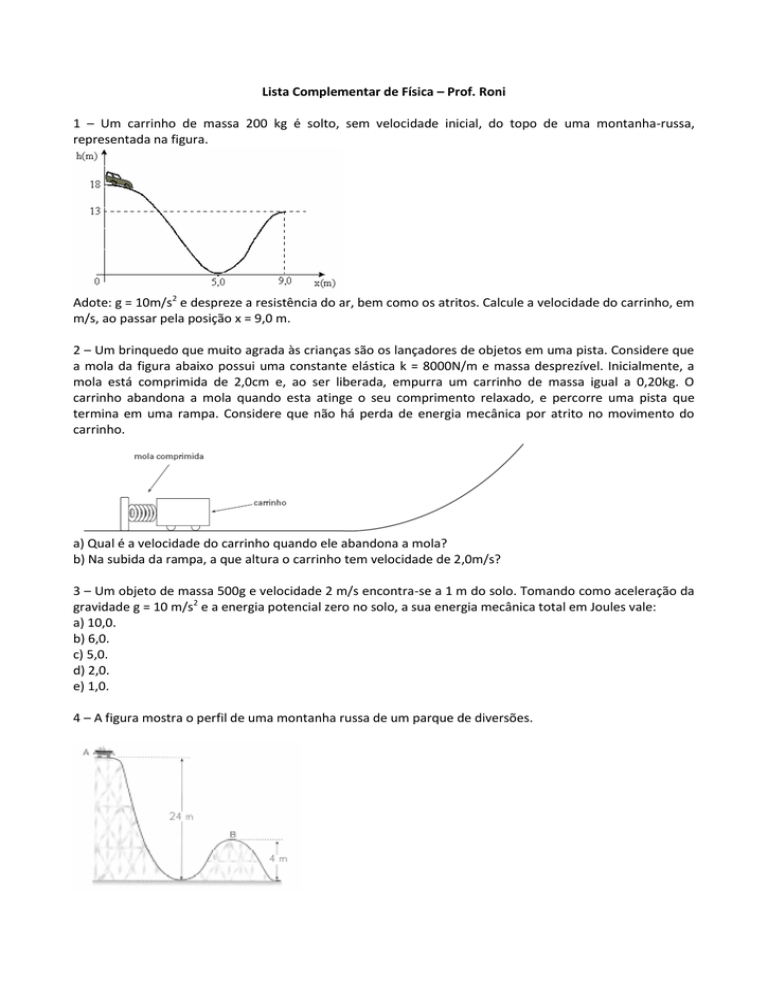
1 – Um carrinho de massa 200 kg é solto, sem velocidade inicial, do topo de uma montanha-russa,
representada na figura.
Adote: g = 10m/s2 e despreze a resistência do ar, bem como os atritos. Calcule a velocidade do carrinho, em
m/s, ao passar pela posição x = 9,0 m.
2 – Um brinquedo que muito agrada às crianças são os lançadores de objetos em uma pista. Considere que
a mola da figura abaixo possui uma constante elástica k = 8000N/m e massa desprezível. Inicialmente, a
mola está comprimida de 2,0cm e, ao ser liberada, empurra um carrinho de massa igual a 0,20kg. O
carrinho abandona a mola quando esta atinge o seu comprimento relaxado, e percorre uma pista que
termina em uma rampa. Considere que não há perda de energia mecânica por atrito no movimento do
carrinho.
a) Qual é a velocidade do carrinho quando ele abandona a mola?
b) Na subida da rampa, a que altura o carrinho tem velocidade de 2,0m/s?
3 – Um objeto de massa 500g e velocidade 2 m/s encontra-se a 1 m do solo. Tomando como aceleração da
gravidade g = 10 m/s2 e a energia potencial zero no solo, a sua energia mecânica total em Joules vale:
a) 10,0.
b) 6,0.
c) 5,0.
d) 2,0.
e) 1,0.
4 – A figura mostra o perfil de uma montanha russa de um parque de diversões.
O carrinho é levado até o ponto mais alto por uma esteira, atingindo o ponto A com velocidade que pode
ser considerada nula. A partir desse ponto, inicia seu movimento e ao passar pelo ponto B sua velocidade é
de 10 m/s. Considerando a massa do conjunto carrinho + passageiros como 400 kg, pode-se afirmar que o
módulo da energia mecânica dissipada pelo sistema foi de:
a) 96 000 J
b) 60 000 J
c) 36 000 J
d) 9 600 J
e) 6 000 J
5 – Um bloco de massa 2,0 kg sobe a rampa ilustrada na figura abaixo, comprimindo uma mola de
constante elástica k = 200 N/m, até parar em B.
Sabe-se que a velocidade do bloco em A era 8,0 m/s e que não houve quaisquer efeitos dissipativos no
trecho entre os pontos A e B. Considerando-se a aceleração da gravidade local igual a 10 m/s2, pode-se
afirmar que a compressão máxima da mola terá sido:
a) 0,60 m
b) 0,65 m
c) 0,50 m
d) 0,80 m
e) 0,85 m
6 – Considere dois blocos A e B, com massas MA e MB respectivamente, em um plano inclinado, como
apresentado na figura.
Desprezando forças de atrito, representando a aceleração da gravidade por g e utilizando dados da tabela:
a) determine a razão MA/MB para que os blocos A e B permaneçam em equilíbrio estático.
b) determine a razão MA/MB para que o bloco A desça o plano com aceleração g/4.
7 – Um bloco de massa 2,0 kg repousa sobre outro de massa 3,0 kg, que pode deslizar sem atrito sobre uma
superfície plana e horizontal. Quando uma força de intensidade 2,0 N, agindo na direção horizontal, é
aplicada ao bloco inferior, como mostra a figura, o conjunto passa a se movimentar sem que o bloco
superior escorregue sobre o inferior. Nessas condições, determine:
a) a aceleração do conjunto.
b) a intensidade da força de atrito entre os dois blocos.
8 – Dois blocos, A e B, com A colocado sobre B, estão em movimento sob ação de uma força horizontal de
4,5 N aplicada sobre A, como ilustrado na figura. Considere que não há atrito entre o bloco B e o solo e que
as massas são respectivamente mA = 1,8 kg e mB = 1,2 kg. Tomando g = 10 m/s2, calcule:
a) a aceleração dos blocos, se eles se locomovem juntos.
b) o valor mínimo do coeficiente de atrito estático para que o bloco A não
deslize sobre B.
9 – Três blocos, 1, 2 e 3, de massas respectivamente iguais a m 1, m2 e m3, encontram-se sobre um plano
horizontal, podendo se deslocar sem atrito. Os blocos estão sob ação da aceleração da gravidade e de uma
força, como mostra a figura. Determine a aceleração do sistema e a força F23 que o bloco 2 exerce sobre o
bloco 3, em função de F, m1, m2 e m3.
10 – Um rebocador puxa duas barcaças pelas águas de um lago tranquilo. A primeira delas tem massa de 30
toneladas e a segunda, 20 toneladas. Por uma questão de economia, o cabo de aço I que conecta o
rebocador à primeira barcaça suporta, no máximo, 6 × 105 N, e o cabo II, 8 × 104 N.
Desprezando o efeito de forças resistivas, calcule a aceleração máxima do conjunto, a fim de evitar o
rompimento de um dos cabos.
11 – Durante a Olimpíada 2000, em Sidney, um atleta de salto em altura, de 60 kg, atingiu a altura máxima
de 2,10m, aterrizando a 3m do seu ponto inicial. Qual o trabalho realizado pelo peso durante a sua
descida? (g=10m/s2)
a) 1800 J
b) 1260 J
c) 300 J
d) 180 J
e) 21 J
12 – A figura representa o gráfico do módulo F de uma força que atua sobre um corpo em função do seu
deslocamento x. Sabe-se que a força atua sempre na mesma direção e sentido do deslocamento.
Pode-se afirmar que o trabalho dessa força no trecho representado pelo gráfico é, em joules,
a) 0.
b) 2,5.
c) 5,0.
d) 7,5.
e) 10.
13 – Um automóvel, de massa 1,0.103 kg, que se move com velocidade de 72 km/h é freado e desenvolve,
então, um movimento uniformemente retardado, parando após percorrer 50 m. O módulo do trabalho
realizado pela força de atrito entre os pneus e a pista durante o retardamento, em joules, foi de
a)5,0.104
b)2,0.104
c)5,0.105
d)2,0.105
e)5,0.106
14 – A partir do repouso, um jovem puxa um caixote de 20kg, que está apoiado sobre uma superfície lisa
horizontal, por meio de uma corda esticada paralelamente à direção do deslocamento (figura abaixo). O
gráfico mostra a variação da intensidade da força aplicada sobre o caixote em função da distância x
percorrida por ele. A velocidade do caixote, ao percorrer 10m, é:
a) 1,0m/s
b) 1,5m/s
c) 2,0m/s
d) 2,5m/s
e) 3,0m/s
15 – Um corpo de massa m = 1,0 kg é solto no ponto A de uma superfície e desliza, sem atrito, até atingir o
ponto B. A partir deste ponto o corpo desloca-se numa superfície horizontal com atrito, até parar no ponto
C, a 5 metros de B.
Sendo m medido em quilogramas e h = 2,0 m, o valor da força de atrito F, suposta constante enquanto o
corpo se movimenta, vale em newtons. (Considere: g = 10 m/s2 ).
a) F = 1 N
b) F = 2 N
c) F = 4 N
d) F = 5 N
e) F = 10 N
Gabarito:
1 – 10 m/s
2 – v = 4 m/s e h = 0,6 m
3–B
4–B
5–A
6 – a) 2 e b) 5
7 – a) 0,4 m/s2 b) 0,8 N
8 – a) 1,5 m/s2 – b) 0,1
9 – a = F/m1+ m2+ m3 e F23 = m3F/m1+ m2+ m3
10 – 4,0 m/s2
11 – B
12 – C
13 – D
14 – E
15 – C