1. (Ufg 2013) Baseado nas propriedades ondulatórias

LISTA - MU – 2ª SÉRIE
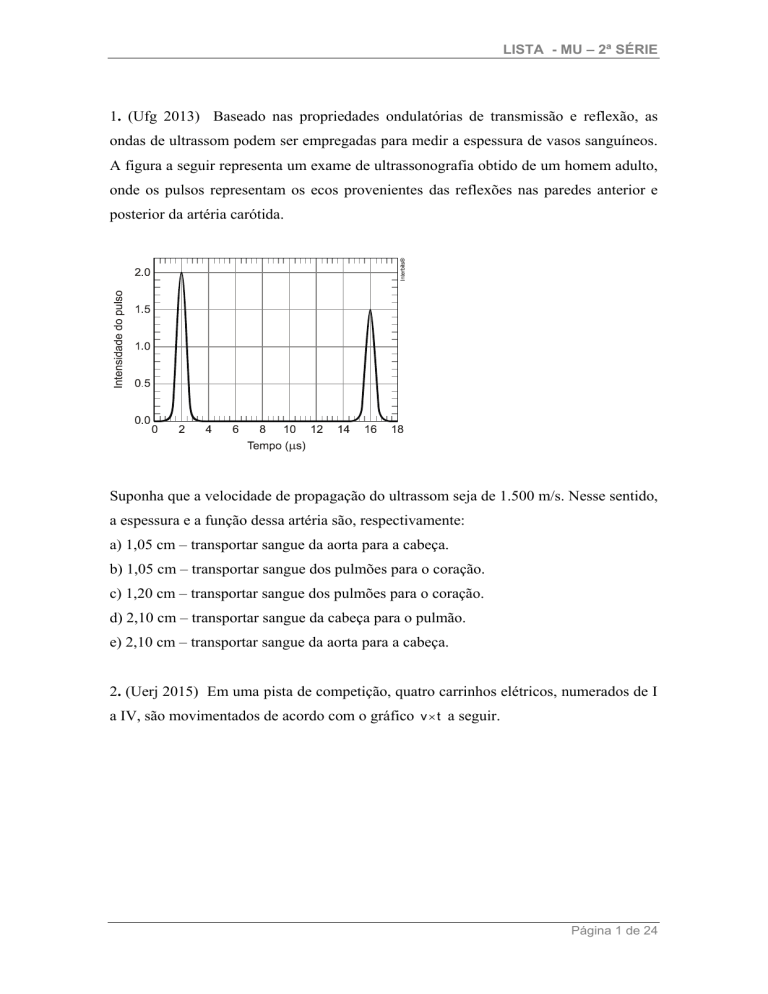
1. (Ufg 2013) Baseado nas propriedades ondulatórias de transmissão e reflexão, as
ondas de ultrassom podem ser empregadas para medir a espessura de vasos sanguíneos.
A figura a seguir representa um exame de ultrassonografia obtido de um homem adulto,
onde os pulsos representam os ecos provenientes das reflexões nas paredes anterior e
posterior da artéria carótida.
Suponha que a velocidade de propagação do ultrassom seja de 1.500 m/s. Nesse sentido,
a espessura e a função dessa artéria são, respectivamente:
a) 1,05 cm – transportar sangue da aorta para a cabeça.
b) 1,05 cm – transportar sangue dos pulmões para o coração.
c) 1,20 cm – transportar sangue dos pulmões para o coração.
d) 2,10 cm – transportar sangue da cabeça para o pulmão.
e) 2,10 cm – transportar sangue da aorta para a cabeça.
2. (Uerj 2015) Em uma pista de competição, quatro carrinhos elétricos, numerados de I
a IV, são movimentados de acordo com o gráfico v  t a seguir.
Página 1 de 24
LISTA - MU – 2ª SÉRIE
O carrinho que percorreu a maior distância em 4 segundos tem a seguinte numeração:
a) I
b) II
c) III
d) IV
3. (G1 - cps 2014)
Algumas cidades têm implantado corredores exclusivos para ônibus a fim de diminuir o
tempo das viagens urbanas.
Suponha que, antes da existência dos corredores, um ônibus demorasse 2 horas e 30
minutos para percorrer todo o trajeto de sua linha, desenvolvendo uma velocidade
média de 6 km/h.
Se os corredores conseguirem garantir que a velocidade média dessa viagem aumente
para 20 km/h, o tempo para que um ônibus percorra todo o trajeto dessa mesma linha
será
a) 30 minutos.
Página 2 de 24
LISTA - MU – 2ª SÉRIE
b) 45 minutos.
c) 1 hora.
d) 1 hora e 15 minutos.
e) 1 hora e 30 minutos.
4. (G1 - ifsp 2014) O número Mach é definido como a relação entre a velocidade do
objeto em movimento e a velocidade do som no meio. A velocidade transônica está
entre a velocidade sub e supersônica. O período transônico inicia quando começa a
aparecer uma barreira de ar em volta das asas do avião. Quando finalmente o avião
ultrapassa a velocidade sônica, segue-se um forte estrondo sonoro. Nesse momento, o
avião excede 1 Mach.
A maior diferença de pressão passa para a frente da aeronave. Esta abrupta diferença de
pressão é a chamada onda de choque, que se estende da traseira à dianteira com uma
forma de cone. Esta onda de choque causa o “boom sônico” que se ouve logo após a
passagem do avião. Quanto maior a velocidade, mais limitado é o denominado cone de
Mach.
Podemos dizer que o texto acima refere-se ao avião com uma velocidade acima de:
a) 360 km/h, velocidade aproximada máxima de um carro de Fórmula 1.
b) 1000 km/h, velocidade aproximada máxima do ar.
c) 1200 km/h, velocidade aproximada máxima do som no ar.
d) 2400 km/h, velocidade aproximada máxima do som no vácuo.
e) 3400 km/h, velocidade aproximada máxima do som na água.
5. (Uea 2014) Com aproximadamente 6 500 km de comprimento, o rio Amazonas
disputa com o rio Nilo o título de rio mais extenso do planeta. Suponha que uma gota de
água que percorra o rio Amazonas possua velocidade igual a 18 km/h e que essa
velocidade se mantenha constante durante todo o percurso. Nessas condições, o tempo
aproximado, em dias, que essa gota levaria para percorrer toda a extensão do rio é
a) 20.
b) 35.
c) 25.
d) 30.
Página 3 de 24
LISTA - MU – 2ª SÉRIE
e) 15.
6. (Uerj 2014) O cérebro humano demora cerca de 0,36 segundos para responder a um
estímulo. Por exemplo, se um motorista decide parar o carro, levará no mínimo esse
tempo de resposta para acionar o freio.
Determine a distância que um carro a 100 km/h percorre durante o tempo de resposta do
motorista e calcule a aceleração média imposta ao carro se ele para totalmente em 5
segundos.
TEXTO PARA A PRÓXIMA QUESTÃO:
Rússia
envia
navios
de
guerra
para
o
Mediterrâneo.
Fonte militar disse que envio ocorre devido à situação na Síria. A Marinha negou que
a movimentação esteja ligada à crise em Damasco.
29/08/2013 08h32 - Atualizado em 29/08/2013 08h32
A Rússia está enviando dois navios de guerra ao Mediterrâneo Oriental, enquanto
potências ocidentais se preparam para uma ação militar na Sina em resposta ao suposto
ataque com armas químicas na semana passada.
Uma fonte anônima do comando das Forças Armadas disse que um cruzador de mísseis
e um navio antissubmarino chegariam aos próximos dias ao Mediterrâneo por causa da
“situação bem conhecida” – uma clara referência ao conflito na Síria.
A Marinha negou que a movimentação esteja ligada aos eventos na Síria e disse que faz
parte de uma rotatividade planejada de seus navios no Mediterrâneo. A força não disse
que tipo de embarcações, ou quantas, estão a caminho da região.
Os Estados Unidos acusam as forças do governo sírio de realizar um ataque com armas
químicas na semana passada e disse que está reposicionando suas forças navais no
Mediterrâneo.
(Portal G1 – http://g1.globo.com/revoIta-arabe/noticia/2013/08/russia-enva-navios-deguerra-para-o-mediterraneo-diz-agencia.htrnIAcesso em 30/0912013)
Página 4 de 24
LISTA - MU – 2ª SÉRIE
7. (G1 - cftrj 2014) A velocidade dos navios é geralmente medida em uma unidade
chamada nó. Um nó equivale a uma velocidade de aproximadamente 1,8 km/h.
Um navio russo que desenvolvesse uma velocidade constante de 25 nós, durante 10
horas, percorreria uma distância de:
a) 180 km.
b) 250 km.
c) 430 km.
d) 450 km.
8. (G1 - ifsp 2013) O jamaicano Usain Bolt, durante as Olimpíadas de 2012 em
Londres, bateu o recorde olímpico da prova dos 100 metros rasos atingindo a marca dos
9,63 segundos. Durante a fase de aceleração, ele conseguiu atingir, aproximadamente, a
máxima velocidade de 44,28 km/h (12,3 m/s) durante os 6 primeiros segundos. A
seguir, o gráfico da velocidade pelo tempo registra esse feito.
De acordo com o gráfico, pode-se afirmar que a aceleração média de Usain Bolt,
durante os primeiros 6 segundos, foi, em m/s2, de
a) 2,05.
b) 2,50.
c) 3,05.
d) 4,50.
e) 5,10.
9. (Pucrj 2013) Na Astronomia, o Ano-luz é definido como a distância percorrida pela
luz no vácuo em um ano. Já o nanômetro, igual a 1,0  10–9 m, é utilizado para medir
distâncias entre objetos na Nanotecnologia.
Considerando que a velocidade da luz no vácuo é igual a 3,0  108 m/s e que um ano
possui 365 dias ou 3,2  107 s, podemos dizer que um Ano-luz em nanômetros é igual a:
Página 5 de 24
LISTA - MU – 2ª SÉRIE
a) 9,6  1024
b) 9,6  1015
c) 9,6  1012
d) 9,6  106
e) 9,6  10–9
10. (G1 - cftmg 2013) O quadro seguinte mostra a velocidade média de corrida de
alguns animais.
ANIMAIS
VELOCIDADE MÉDIA
cavalo
1,24 km/min
coelho
55 km/h
girafa
833 m/min
zebra
18 m/s
Disponível
<http://curiosidades.tripod.com/velocidade.htm>.
em:
Acesso
em: 11 out. 2012.
(Adaptado).
Dentre os animais citados, o que possui maior velocidade média é a(o)
a) cavalo.
b) coelho.
c) girafa.
d) zebra.
11. (Pucrj 2013) O gráfico da figura mostra a posição em função do tempo de uma
pessoa que passeia em um parque.
Página 6 de 24
LISTA - MU – 2ª SÉRIE
Calcule a velocidade média em m/s desta pessoa durante todo o passeio, expressando o
resultado com o número de algarismos significativos apropriados.
a) 0,50
b) 1,25
c) 1,50
d) 1,70
e) 4,00
12. (Unicamp 2013) Para fins de registros de recordes mundiais, nas provas de 100
metros rasos não são consideradas as marcas em competições em que houver vento
favorável (mesmo sentido do corredor) com velocidade superior a 2 m s. Sabe-se que,
com vento favorável de 2 m s, o tempo necessário para a conclusão da prova é reduzido
em 0,1 s. Se um velocista realiza a prova em 10 s sem vento, qual seria sua velocidade
se o vento fosse favorável com velocidade de 2 m s?
a) 8,0 m/s.
b) 9,9 m/s.
c) 10,1 m/s.
d) 12,0 m/s.
13. (Uern 2013) Seja o gráfico da velocidade em função do tempo de um corpo em
movimento retilíneo uniformemente variado representado abaixo.
Página 7 de 24
LISTA - MU – 2ª SÉRIE
Considerando a posição inicial desse movimento igual a 46 m, então a posição do corpo
no instante t = 8 s é
a) 54 m.
b) 62 m.
c) 66 m.
d) 74 m.
14. (Uern 2013) O gráfico abaixo representa a variação da velocidade de um móvel em
função do tempo.
Se o deslocamento efetuado pelo móvel nos 10 s do movimento e igual a 40 m, então a
velocidade inicial v 0 e igual a
a) 4 m/s.
b) 5 m/s.
c) 6 m/s.
d) 7 m/s.
15. (G1 - cps 2012) Em uma determinada cidade, a malha metroviária foi concebida de
modo que a distância entre duas estações consecutivas seja de 2,4 km. Em toda a sua
Página 8 de 24
LISTA - MU – 2ª SÉRIE
extensão, a malha tem 16 estações, e o tempo necessário para ir-se da primeira à última
estação é de 30 minutos.
Nessa malha metroviária, a velocidade média de um trem que se movimenta da primeira
até a última estação é, em km/h, de
a) 72.
b) 68.
c) 64.
d) 60.
e) 56.
16. (Espcex (Aman) 2012) Um automóvel percorre a metade de uma distância D com
uma velocidade média de 24 m s e a outra metade com uma velocidade média de 8 m s.
Nesta situação, a velocidade média do automóvel, ao percorrer toda a distância D, é de:
a) 12 m s
b) 14 m s
c) 16 m s
d) 18 m s
e) 32 m s
17. (Pucrj 2012) Uma pessoa caminha sobre uma estrada horizontal e retilínea até
chegar ao seu destino. A distância percorrida pela pessoa é de 2,5 km, e o tempo total
foi de 25 min.
Qual o módulo da velocidade da pessoa?
a) 10 m/s
b) 6,0 km/h
c) 10 km/h
Página 9 de 24
LISTA - MU – 2ª SÉRIE
d) 6,0 m/s
e) 10 km/min
18. (G1 - ifsp 2012) Em um trecho retilíneo de estrada, dois veículos, A e B, mantêm
velocidades constantes VA  14 m/s e VB  54 km/h .
Sobre os movimentos desses veículos, pode-se afirmar que
a) ambos apresentam a mesma velocidade escalar.
b) mantidas essas velocidades, A não conseguirá ultrapassar B.
c) A está mais rápido do que B.
d) a cada segundo que passa, A fica dois metros mais distante de B.
e) depois de 40 s A terá ultrapassado B.
19. (Feevale 2012) Na região Amazônica, os rios são muito utilizados para transporte.
Considere que João se encontra na cidade A e pretende se deslocar até a cidade B de
canoa. Conforme indica a figura, João deve passar pelos pontos intermediários 1, 2 e 3.
Considere as distâncias (D) mostradas no quadro que segue.
Página 10 de 24
LISTA - MU – 2ª SÉRIE
Trechos D (km)
A até 1
2
1 até 2
4
2 até 3
4
3 até B
3
João sai da cidade A às 7h e passa pelo ponto 1 às 9h. Se mantiver a velocidade
constante em todo o trajeto, a que horas chegará a B?
a) 13 h
b) 14 h
c) 16 h
d) 18 h
e) 20 h
20. (Unisinos 2012) A figura abaixo ilustra trechos de algumas ruas de uma região
plana de uma cidade. Uma pessoa que caminha com velocidade escalar constante de
5,4 km h 1,5 m s 
necessita ir do ponto A ao ponto B.
Caminhando sobre as linhas pontilhadas, o menor intervalo de tempo possível para essa
caminhada é, aproximadamente, em segundos, de
a) 106.
b) 120.
c) 380.
d) 433.
e) 855.
Página 11 de 24
LISTA - MU – 2ª SÉRIE
21. (Uespi 2012) Um motorista em seu automóvel deseja ir do ponto A ao ponto B de
uma grande cidade (ver figura). O triângulo ABC é retângulo, com os catetos AC e CB
de comprimentos 3 km e 4 km, respectivamente. O Departamento de Trânsito da cidade
informa que as respectivas velocidades médias nos trechos AB e ACB valem 15 km/h e
21 km/h. Nessa situação, podemos concluir que o motorista:
a) chegará 20 min mais cedo se for pelo caminho direto AB.
b) chegará 10 min mais cedo se for pelo caminho direto AB.
c) gastará o mesmo tempo para ir pelo percurso AB ou pelo percurso ACB.
d) chegará 10 min mais cedo se for pelo caminho ACB.
e) chegará 20 min mais cedo se for pelo caminho ACB.
22. (Espcex (Aman) 2012)
O gráfico abaixo representa a velocidade(v) de uma
partícula que se desloca sobre uma reta em função do tempo(t). O deslocamento da
partícula, no intervalo de 0 s a 8 s, foi de:
a) –32 m
b) –16 m
c) 0 m
Página 12 de 24
LISTA - MU – 2ª SÉRIE
d) 16 m
e) 32 m
23. (Uel 2011)
A cronometragem precisa das provas de atletismo envolve vários
equipamentos, entre eles, a associação de emissores e sensores de radiação.
De acordo com os conhecimentos de física moderna relacionados com emissores e
sensores de radiação, assinale a alternativa correta.
a) Para fins práticos, o sensor detecta instantaneamente o bloqueio da radiação devido à
elevada velocidade da luz com relação à do atleta.
b) Os sensores interagem com a radiação por meio do efeito piezoelétrico.
c) Os lasers, utilizados como emissores, caracterizam-se pela absorção simulada da
radiação.
d) A intensidade de radiação emitida por um emissor laser é diretamente proporcional à
distância que o separa do sensor.
e) A radiação de um emissor laser será detectada se sua energia for metade da energia
de excitação do sensor.
24. (Unimontes 2011) Dois aviões do grupo de acrobacias (Esquadrilha da Fumaça) são
capazes de realizar manobras diversas e deixam para trás um rastro de fumaça. Nessas
condições, para que os aviões descrevam duas semirretas paralelas verticais
(perpendiculares ao solo, considerado plano), de tal sorte que o desenho fique do
mesmo tamanho, os pilotos controlam os aviões para que tenham velocidades
constantes e de mesmo módulo.
Considerando o mesmo sentido para o movimiento dos aviões durante essa acrobacia,
pode-se afirmar corretamente que
a) os aviões não se movimentam em relação ao solo.
b) os aviões estão parados, um em relação ao outro.
c) um observador parado em relação ao solo está acelerado em relação aos aviões.
d) um avião está acelerado em relação ao outro.
25. (Epcar (Afa) 2011)
Dois automóveis A e B encontram-se estacionados
paralelamente ao marco zero de uma estrada. Em um dado instante, o automóvel A
parte, movimentando-se com velocidade escalar constante VA = 80 km/h. Depois de
Página 13 de 24
LISTA - MU – 2ª SÉRIE
certo intervalo de tempo, Δt , o automóvel B parte no encalço de A com velocidade
escalar constante VB = 100 km/h. Após 2 h de viagem, o motorista de A verifica que B
se encontra 10 km atrás e conclui que o intervalo Δt , em que o motorista B ainda
permaneceu estacionado, em horas, é igual a
a) 0,25
b) 0,50
c) 1,00
d) 4,00
Página 14 de 24
LISTA - MU – 2ª SÉRIE
Gabarito:
Resposta da questão 1:
[A]
[Resposta do ponto de vista da disciplina de Biologia]
As artérias carótidas transportam sangue arterial da aorta para a cabeça.
[Resposta do ponto de vista da disciplina de Física]
Do gráfico, a diferença de tempo entre as duas recepções é:
Δt  16  2  14 μs  14  106 s.
A distância percorrida (d) nesse intervalo de tempo é igual a duas vezes a espessura (e)
da artéria. Assim:
d  v Δt  2 e  v Δt  e 
v Δt 1500  14  106

 1,05  102 m 
2
2
e  1,05 cm.
Resposta da questão 2:
[B]
No gráfico v  t, a distância percorrida é obtida pela ”área" entre a linha do gráfico e o
eixo dos tempos. Calculando cada uma delas:
Página 15 de 24
LISTA - MU – 2ª SÉRIE

 2  0,5 1
2  0,5

 1 2  0,5  1,25  2  3,75 m.
DI 
2
2





1,5  1 2
1 1

 1,5  1  0,5  2,5  1,5  4,5 m.
DII 
2
2





2 1
 2  1  1  2  3 m.
DIII 
2





D  3  0,5   0,5  11  0,75  0,75  1,5 m.
 IV
2
2
Resposta da questão 3:
[B]
Dados v1  6km / h; v2  20km / h; Δt1  2h e 30min  150min.
O espaço percorrido é o mesmo nos dois casos.
ΔS1  ΔS2  v1 Δt1  v 2 Δt 2  6  150  20  Δt 2  Δt 2 
900

20
Δt 2  45 min.
Resposta da questão 4:
[C]
A velocidade de propagação do som no ar é cerca de 340 m/s. Passando para km/h:
v  340
m 0,34 km

 0,34  3.600 km/h 
1
s
h
3.600
v  1.224 km/h
Resposta da questão 5:
[E]
Página 16 de 24
LISTA - MU – 2ª SÉRIE
Δt 
ΔS 6.500
360

 360 h  Δt 
v
18
24

Δt  15 dias
Resposta da questão 6:
 Distância percorrida durante o tempo de resposta:
Dados: v = 100 km/h = (100/3,6) m/s; Δt  0,36s.
D  v Δt 
100
 0,36  D  10 m.
3,6
 Aceleração média de frenagem:
Dados: v0 = 100 km/h = (100/3,6) m/s; v = 0; Δt  5s.
Supondo trajetória retilínea, a aceleração escalar é:
a
100
Δv 0 
3,6

 a  5,6 m/s2 .
Δt
5
Resposta da questão 7:
[D]
d  v Δ t  25  1,8  10

d  450 km.
Resposta da questão 8:
[A]
Aplicando a definição de aceleração escalar média:
am 
Δv 12,3  0

Δt
6
 am  2,05 m / s2.
Resposta da questão 9:
[A]
Página 17 de 24
LISTA - MU – 2ª SÉRIE
V
ΔS
ΔS
 3x108 
 ΔS  9,6x1015 m  9,6x1024 m
Δt
3,2x107
Resposta da questão 10:
[A]
Expressando todas as velocidades no SI, conclui-se que o cavalo é o animal mais
rápido, conforme destaque na tabela.
VELOCIDADE
ANIMAIS
VELOCIDADE MÉDIA
cavalo
1,24 km/min
20,7
coelho
55 km/h
15,2
girafa
833 m/min
13,9
zebra
18 m/s
18,0
MÉDIA
(m/s)
Resposta da questão 11:
[B]
Vm 
ΔS 50  0

 1,25 m/s.
Δt 40  0
Resposta da questão 12:
[C]
Velocidade média do atleta com a ajuda do vento:
Δs 100m

Δt
9.9s
v  10.1m s
v
Página 18 de 24
LISTA - MU – 2ª SÉRIE
Resposta da questão 13:
[B]
Dado: S0 = 46 m.
Do gráfico:
t  0  v 0  10 m/s



t  5 s  v  0
 a
Δv 0  10

 a  2 m/s2 .
Δt
50
Aplicando a função horária do espaço para o instante t = 8 s:
S  S0  v 0 t 
a 2
2
t  S  46  10  8  
8 2  46  80  64 
2
2
S  62 m.
Resposta da questão 14:
[B]
A área do trapézio entre a linha do gráfico e o eixo dos tempos é numericamente igual
ao deslocamento efetuado.
40 
10  6
80
v0  v0 
2
16

v0  5 m/s.
Resposta da questão 15:
[A]
Da definição de velocidade escalar média:
vm 
ΔS 15  2,4  36


Δt
0,5
0,5
 vm  72 km / h.
Página 19 de 24
LISTA - MU – 2ª SÉRIE
Resposta da questão 16:
[A]
Vm 
ΔS
Δt
Primeiro trecho
24 
D/2
D
 Δt 1
Δt1
48
Segundo trecho
8
D/2
D
 Δt 1
Δt1
16
Movimento todo
Δt  Δt1  Δt 2 
Vm 
D D
D


48 16 12
D
 12 m/s
D / 12
Resposta da questão 17:
[B]
V
ΔS 2,5

 0,1km / min  6,0km / h
Δt
25
Resposta da questão 18:
[B]
Página 20 de 24
LISTA - MU – 2ª SÉRIE
Dados: VA = 14 m/s; VB = 54 km/h = 15 m/s.
Como a velocidade de A é menor que a de B, A não conseguirá ultrapassar B.
Resposta da questão 19:
[E]
A velocidade no trecho A1 = 2 km é igual à velocidade no trecho AB = (2 + 4 + 4 + 3)
= 13 km.

ΔSA1
v A1 


97

ΔSAB
v

AB

t 7


2
13

 t  7  13  t  20 h.
2 t 7
Resposta da questão 20:
[C]
Sendo a velocidade constante, em módulo, o menor tempo é aquele em o caminho é o
mais curto (ACB), mostrado na figura.
Página 21 de 24
LISTA - MU – 2ª SÉRIE
Para calcular a distāncia DCB, aplicamos Pitįgoras:
2
DCB
 1202  1602  14400  25600  40000  DCB  40000 
DCB  200 m.
Calculando a distāncia ACB:
DACB  370  200  570 m.
Entćo o tempo mķnimo é:
Δt 
DACB 570

v
1,5
 Δt  380 s.
Resposta da questão 21:
[C]
Dados: vAB = 15 km/h; vACB = 21 km/h.
Aplicando Pitágoras no triângulo dado:
uuur
uuur
uuur
| AB |2 | AC |2  | CB |2

uuur
| AB |2  9  16  25 
uuur
| AB | 5 km.
Calculando os tempos:
uuur

| AB | 5
1


h  Δt AB  20 min.
Δt AB 
v AB
15 3

uuur
uuur

| AC |  | BC | 3  4 1
Δt


h  Δt ACB  20 min.
 ACB 
v ACB
21
3

 Δt ACB  Δt AB  20 min.
Resposta da questão 22:
[C]
Página 22 de 24
LISTA - MU – 2ª SÉRIE
As áreas da figura abaixo representam o deslocamento. Como uma é positiva e a outra
negativa de mesmo módulo, o deslocamento total é nulo.
Resposta da questão 23:
[A]
A figura mostra uma pista de atletismo onde correm 8 atletas.
Quando o primeiro atinge a linha de chegada ele interrompe a passagem do laser e seu
tempo é registrado. Entenda que, como a velocidade de uma radiação eletromagnética é
muito alta, o tempo de propagação do laser do emissor ao receptor é desprezível.
Resposta da questão 24:
[B]
Página 23 de 24
LISTA - MU – 2ª SÉRIE
Como, em relação ao solo, suas velocidades são iguais, um avião está em repouso em
relação ao outro.
Resposta da questão 25:
[B]
Dados: vA = 80 km/h; vB = 100 km/h; D = 10 km; tA = 2 h.
Como ambos são movimentos uniformes, considerando a origem no ponto de partida,
temos:

SA  v A t A  SA  80t A


SB  vB tB  SB  100tB
Após 2 h (tA = 2 h) a distância entre os dois automóveis é 10 km, estando B atrás.
Então:
SA  SB  10  80t A  100 tB  10  80  2   100 t B  10  150  100 t B 
tB  1,5 h.
Mas:
t  t A  tB  2  1,5  t  0,5 h.
Página 24 de 24