MU – Movimento Uniforme

MU
1. (Uerj 2013) Um motorista dirige um automóvel em um trecho plano de um viaduto. O
movimento é retilíneo e uniforme.
A intervalos regulares de 9 segundos, o motorista percebe a passagem do automóvel sobre
cada uma das juntas de dilatação do viaduto.
Sabendo que a velocidade do carro é 80 km/h, determine a distância entre duas juntas
consecutivas.
2. (G1 - ifsp 2012) Em um trecho retilíneo de estrada, dois veículos, A e B, mantêm
velocidades constantes VA  14 m/s e VB  54 km/h .
Sobre os movimentos desses veículos, pode-se afirmar que
a) ambos apresentam a mesma velocidade escalar.
b) mantidas essas velocidades, A não conseguirá ultrapassar B.
c) A está mais rápido do que B.
d) a cada segundo que passa, A fica dois metros mais distante de B.
e) depois de 40 s A terá ultrapassado B.
3. (Uespi 2012) Um motorista em seu automóvel deseja ir do ponto A ao ponto B de uma
grande cidade (ver figura). O triângulo ABC é retângulo, com os catetos AC e CB de
comprimentos 3 km e 4 km, respectivamente. O Departamento de Trânsito da cidade informa
que as respectivas velocidades médias nos trechos AB e ACB valem 15 km/h e 21 km/h. Nessa
situação, podemos concluir que o motorista:
a) chegará 20 min mais cedo se for pelo caminho direto AB.
b) chegará 10 min mais cedo se for pelo caminho direto AB.
c) gastará o mesmo tempo para ir pelo percurso AB ou pelo percurso ACB.
d) chegará 10 min mais cedo se for pelo caminho ACB.
e) chegará 20 min mais cedo se for pelo caminho ACB.
www.nsaulasparticulares.com.br
Página 1 de 8
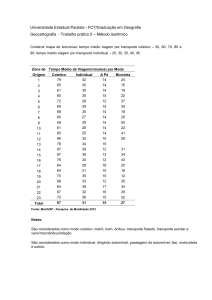
4. (Feevale 2012) Na região Amazônica, os rios são muito utilizados para transporte.
Considere que João se encontra na cidade A e pretende se deslocar até a cidade B de canoa.
Conforme indica a figura, João deve passar pelos pontos intermediários 1, 2 e 3. Considere as
distâncias (D) mostradas no quadro que segue.
Trechos
A até 1
1 até 2
2 até 3
3 até B
D (km)
2
4
4
3
João sai da cidade A às 7h e passa pelo ponto 1 às 9h. Se mantiver a velocidade constante em
todo o trajeto, a que horas chegará a B?
a) 13 h
b) 14 h
c) 16 h
d) 18 h
e) 20 h
5. (Unisinos 2012) A figura abaixo ilustra trechos de algumas ruas de uma região plana de
uma cidade. Uma pessoa que caminha com velocidade escalar constante de 5,4 km h
1,5 m s
necessita ir do ponto A ao ponto B.
Caminhando sobre as linhas pontilhadas, o menor intervalo de tempo possível para essa
caminhada é, aproximadamente, em segundos, de
a) 106.
b) 120.
c) 380.
d) 433.
e) 855.
www.nsaulasparticulares.com.br
Página 2 de 8
6. (G1 - cps 2010) Considere que Roberto, em suas caminhadas de 2 000 m para manter o
seu condicionamento físico, desenvolva uma velocidade média de 5 km/h.
O tempo gasto para percorrer esta distância é de
a) 12 min.
b) 20 min.
c) 24 min.
d) 36 min.
e) 40 min.
7. (Pucrj 2010) Uma tartaruga caminha, em linha reta, a 40 metros/hora, por um tempo de 15
minutos. Qual a distância percorrida?
a) 30 m
b) 10 km
c) 25 m
d) 1 km
e) 10 m
8. (Pucrj 2010) O tempo entre observarmos um raio e escutarmos o som emitido por ele pode
ser utilizado para determinar a distância entre o observador e a posição onde “caiu” o raio. Se
levarmos 3 s para escutar o relâmpago é correto afirmar que o raio caiu a: (Considere a
velocidade do som no ar como 340 m/s)
a) 340 m.
b) 680 m.
c) 1.020 m.
d) 1.360 m.
e) 1.700 m.
9. (Uerj 2010) Dois automóveis, M e N, inicialmente a 50 km de distância um do outro,
deslocam-se com velocidades constantes na mesma direção e em sentidos opostos. O valor da
velocidade de M, em relação a um ponto fixo da estrada, é igual a 60 km/h. Após 30 minutos,
os automóveis cruzam uma mesma linha da estrada.
Em relação a um ponto fixo da estrada, a velocidade de N tem o seguinte valor, em quilômetros
por hora:
a) 40
b) 50
c) 60
d) 70
10. (Pucrj 2010) Um pássaro voa em linha reta do ponto A, no solo, ao ponto B, em uma
montanha, que dista
400 m do ponto A ao longo da horizontal. O ponto B se encontra também a uma altura de 300
m em relação ao solo. Dado que a velocidade do pássaro é de 20 m/s, o intervalo de tempo
que ele leva pra percorrer a distância de A a B é de (considere g = 10 m/s 2)
a) 20 s
b) 25 s
c) 35 s
d) 40 s
e) 10 s
11. (G1 1996) Um veículo obedece a equação S = 20 - 4.t, em unidades do sistema
internacional. Qual a posição do corpo, no instante t = 3,0s?
12. (G1 1996) Um carro percorre a distância entre São Paulo e São José dos Campos (90 km)
com velocidade média de 60 km/h; a distância entre São José dos Campos e Cruzeiro (100
km) com velocidade média de 100 km/h e entre Cruzeiro e Rio de Janeiro (210 km) com
velocidade média de 60 km/h. Qual o tempo que levou o carro de São Paulo ao Rio de
Janeiro?
a) 5,5 h.
b) 6,5 h.
c) 6,0 h.
d) 3,5 h.
e) 1,5 h.
www.nsaulasparticulares.com.br
Página 3 de 8
13. (G1 1996) Se um veículo obedece a equação horária S = 3 + 4 . t, em unidades do sistema
internacional, qual o tipo de movimento que ele apresenta, uniforme ou variado?
14. (G1 1996) Qual a velocidade média de um atleta que faz 50 m em 4,0 s?
15. (G1 1996) Um corpo obedece a equação S = 20 - 5 . t, em unidades do sistema
internacional. Este movimento é progressivo ou retrógrado?
16. (G1 1996) A equação horária S = 3 + 4 . t, em unidades do sistema internacional, traduz,
em um dado referencial, o movimento de uma partícula. No instante t = 3 s, qual a velocidade
da partícula?
17. (G1 1996) A equação horária S = 3 + 4 . t, em unidades do sistema internacional, traduz,
em um dado referencial, o movimento de uma partícula. No instante t = 3 s, qual a posição da
partícula?
18. (G1 1996) Um trem de 200 m de comprimento viaja a 20 m/s. Qual o intervalo de tempo
necessário para que este trem ultrapasse um túnel de 300 m de comprimento?
19. (Unitau 1995) Um automóvel percorre uma estrada com função horária s = - 40 + 80t, onde
s é dado em km e t em horas. O automóvel passa pelo km zero após:
a) 1,0 h.
b) 1,5 h.
c) 0,5 h.
d) 2,0 h.
e) 2,5 h.
20. (Fatec 1995) A tabela fornece, em vários instantes, a posição s de um automóvel em
relação ao km zero da estrada em que se movimenta.
A função horária que nos fornece a posição do automóvel, com as unidades fornecidas, é:
a) s = 200 + 30t
b) s = 200 - 30t
c) s = 200 + 15t
d) s = 200 - 15t
e) s = 200 - 15t2
www.nsaulasparticulares.com.br
Página 4 de 8
Gabarito:
Resposta da questão 1:
Δs
80
Δs
v

(m / s) 
Δt
3,6
9(s)
Δs 
9.80
 m
3,6
 Δs  200m
Resposta da questão 2:
[B]
Dados: VA = 14 m/s; VB = 54 km/h = 15 m/s.
Como a velocidade de A é menor que a de B, A não conseguirá ultrapassar B.
Resposta da questão 3:
[C]
Dados: vAB = 15 km/h; vACB = 21 km/h.
Aplicando Pitágoras no triângulo dado:
| AB |2 | AC |2  | CB |2

| AB |2  9  16  25 
| AB | 5 km.
Calculando os tempos:

| AB | 5
1


h  Δt AB  20 min.
Δt AB 
v AB
15 3


| AC |  | BC | 3  4 1
Δt


h  Δt ACB  20 min.
 ACB 
v ACB
21
3

 Δt ACB  Δt AB  20 min.
Resposta da questão 4:
[E]
A velocidade no trecho A1 = 2 km é igual à velocidade no trecho AB = (2 + 4 + 4 + 3) = 13 km.

ΔSA1
v A1 


97

ΔSAB
v
AB 

t 7


2
13

 t  7  13  t  20 h.
2 t 7
Resposta da questão 5:
[C]
Sendo a velocidade constante, em módulo, o menor tempo é aquele em o caminho é o mais
curto (ACB), mostrado na figura.
www.nsaulasparticulares.com.br
Página 5 de 8
Para calcular a distância DCB, aplicamos Pitágoras:
2
DCB
 1202  1602  14400  25600  40000  DCB  40000 
DCB  200 m.
Calculando a distância ACB:
DACB  370  200  570 m.
Então o tempo mínimo é:
D
570
Δt  ACB 
 Δt  380 s.
v
1,5
Resposta da questão 6:
[C]
Dados: v = 5 km/h; S = 2.000 m = 2 km.
S
S 2
v
 t 
  0,4 h  t = 0,4 (60)  t = 24 min.
t
v
5
Resposta da questão 7:
[E]
Dados: v = 40 m/h; t = 15 min =
1
h.
4
 1
S = v t = 40    S = 10 m.
4
Resposta da questão 8:
[C]
O tempo que a luz leva para atingir nossos olhos é desprezível, comparado ao tempo que o
som leva para atingir nossos ouvidos. Então:
D = vsom t = 340 (3)  D = 1.020 m.
www.nsaulasparticulares.com.br
Página 6 de 8
Resposta da questão 9:
[A]
Seja P o ponto de encontro desses dois automóveis, como indicado na figura.
Do instante mostrado até o encontro, que ocorreu no ponto P, passaram-se 30 min ou 0,5 h, a
distância percorrida pelo automóvel M é:
DM = vM t = 60 (0,5) = 30 km.
Nesse mesmo intervalo de tempo, o automóvel N percorreu, então:
DN = 50 – 20 = 30 km.
Assim:
D
20
vN = N 
 vN = 40 km/h.
t 0,5
Resposta da questão 10:
[B]
Da figura:
d2AB  3002  4002 
dAB  250.000

dAB = 500 m.
Supondo que o pássaro voe em linha reta:
dAB = v t  500 = 20 t  t = 25 s.
Resposta da questão 11:
8m
Resposta da questão 12:
[C]
Resposta da questão 13:
Uniforme.
Resposta da questão 14:
12,5 m/s
www.nsaulasparticulares.com.br
Página 7 de 8
Resposta da questão 15:
Retrógrado
Resposta da questão 16:
4 m/s
Resposta da questão 17:
15 m
Resposta da questão 18:
25 s
Resposta da questão 19:
[C]
Resposta da questão 20:
[D]
www.nsaulasparticulares.com.br
Página 8 de 8