P-ICMatemática DiscretaUma nota sobre a caracterização

ISSN 2317-3297
Uma nota sobre a caracterização de grafos de intervalos
próprios de Mertzios
Jorge E. C. Walder∗,
Sheila M. Almeida,
Câmpus de Ponta Porã, UFMS
79907-414, Ponta Porã, MS
E-mail: [email protected], [email protected]
Palavras-chave: grafos de intervalos próprios, caracterização, representação de grafos
Resumo: Em [4] é apresentado um algoritmo que, dada uma representação de um grafo através
de uma famı́lia de intervalos quaisquer, constrói uma representação com a qual se pode reconhecer um grafo de intervalos próprios. Segundo o autor, quando a famı́lia de intervalos
dada na entrada representa um grafo de intervalos próprios, a saı́da é uma representação por
intervalos em que nenhum intervalo contém propriamente um outro. Neste trabalho, mostramos
uma representação por intervalos de um grafo de intervalos próprios que, dada como entrada do
algoritmo, resulta em uma representação por intervalos onde um intervalo contém propriamente
outro. Provamos que, nesse caso, a representação resultante pode ser convertida em uma representação em que nenhum intervalo contém propriamente outro, garantindo a caracterização
apresentada em [4].
1
Introdução
Um conjunto C qualquer contém propriamente um outro conjunto C 0 se, e somente se, C contém
C 0 e C \ C 0 6= ∅. Essa definição se aplica a intervalos da reta real, de forma que um intervalo
[a, b] contém propriamente outro intervalo [c, d] se, e somente se, a < c e b >= d ou a <= c e
b > d. Um grafo G é um grafo de intervalos próprios se, e somente se, G pode ser representado
por uma famı́lia F de intervalos da reta real, tal que cada vértice corresponde a um intervalo
distinto de F, nenhum intervalo de F contém propriamente outro e dois vértices em G são
adjacentes se, e somente se, os intervalos correspondentes tem interseção não-vazia. Os grafos
de intervalos próprios possuem diversas caracterizações. As mais comuns são a de possuirem
uma representação pela interseção de intervalos de tamanho unitário [5] e a de possuirem uma
ordem dos vértices em que vértices da mesma clique maximal são consecutivos [5]. Esta classe
de grafos tem sido bastante estudada [1, 2, 3, 4]. Em [4], Mertzios apresenta um algoritmo que,
dada uma representação de um grafo G através da interseção de intervalos da reta real, gera
uma nova representação por intervalos para o grafo G que satisfaz as propriedades apresentadas
na Definição 1.1.
Definição 1.1 [4] Uma representação de n intervalos é chamada Representação por Intervalos
Normal (RIN), se todos os intervalos são da forma [i, j), 0 ≤ i < j ≤ n, e exatamente um
intervalo começa em i, para todo i ∈ {0, 1, ..., n − 1}.
Usando a RIN resultante da execução do algoritmo, o autor garante que, se a representação
por intervalos dada na entrada corresponder a um grafo de intervalos próprios, então a representação resultante desse algoritmo é uma RIN em Escada, definida a seguir.
∗
Bolsista PET-Fronteira
329
ISSN 2317-3297
Definição 1.2 [4] Uma RIN é uma Representação por Intervalos Normal em Escada (RINE)
se, para todo par de intervalos [a, b) e [c, d) em que a < c, tem-se b ≤ d.
Para caracterizar os grafos de intervalos próprios usando sua RIN, Mertzios prova que quando
a representação por intervalos dada na entrada do algoritmo representa um grafo de intervalos
próprios, a saı́da do algoritmo é uma RINE [4]. Para garantir que obter uma RINE na saı́da
do algoritmo é condição suficiente para que o grafo seja de intervalos próprios, Mertzios diz que
uma RINE é, claramente, uma representação através de interseções de uma famı́lia de intervalos
em que nenhum intervalo contém propriamente outro. Neste trabalho, apresentamos um contraexemplo para essa afirmação e provamos que, ainda assim, a existência da RINE é condição
suficiente para garantir que o grafo representado pela mesma é um grafo de intervalos próprios.
2
Algoritmo de Mertzios
Mertzios [4] apresentou o algoritmo a seguir que, dada uma representação por intervalos, gera
uma RIN onde são preservadas as relações de interseção da famı́lia de intervalos dada na entrada
do algoritmo.
Algoritmo 1 RINE (G)
entrada: uma famı́lia com n intervalos da reta real.
1. Suponha que alguns intervalos tenham exatamente um ponto x ∈ R em comum. Considere
2 > x, o próximo maior ponto onde algum intervalo começa. Considere também 1 < x,
o próximo menor ponto onde algum intervalo termina. Substitua todo intervalo [a, x] pelo
intervalo [a, (x + 2 )/2] e todo intervalo [x, b] pelo intervalo [(x + 1 )/2, b]. Repita esse
passo enquanto possı́vel.
2. Substitua todo intervalo [a, b] pelo intervalo [a, b).
3. Suponha que exatos l > 1 intervalos começam no mesmo ponto a e o próximo maior ponto
onde algum intervalo começa ou termina é o ponto b > a. Mova a extremidade esquerda
do i-ésimo intervalo dos l intervalos do ponto a para o ponto a + (i − 1)(b − a)/l. Repita
esse passo enquanto possı́vel.
4. Suponha que as extremidades esquerdas dos n intervalos são os pontos a1 ≤ a2 ≤ ... ≤ an .
Substitua todo intervalo da forma [aj , b), onde j ≤ i e ai < b < ai+1 , pelo intervalo
[aj , ai+1 ). Substitua também todo intervalo da forma [aj , b) com b ≥ an pelo intervalo
[aj , an + 1).
5. Seja pi um ponto onde pelo menos um intervalo começa ou termina, 0 ≤ i ≤ n. Suponha
que tais pontos estão ordenados: p0 < p1 < ... < pn . Substitua o intervalo [pi , pj ) pelo
intervalo [i, j), 0 ≤ i, j ≤ n.
3
Caracterização dos Grafos de Intervalos Próprios
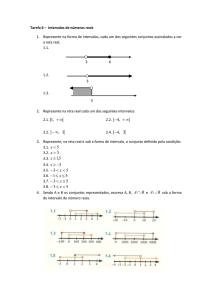
A Figura 1 apresenta um caso em que a famı́lia de intervalos dada na entrada do Algoritmo 1
corresponde a um grafo de intervalos próprios e a RINE resultante é uma famı́lia de intervalos
em que o intervalo b contém propriamente o intervalo c e que o intervalo e contém propriamente
os intervalos f e g ao fim da execução, contradizendo a afirmação de Mertzios [4].
Com o lema a seguir mostramos que qualquer RINE pode ser transformada em uma representação através de interseções de uma famı́lia de intervalos em que nenhum intervalo contém
propriamente outro, preservando-se as interseções entre quaisquer dois intervalos. Logo, toda
RINE representa um grafo de intervalos próprios.
330
ISSN 2317-3297
Saída:
Entrada:
3
2
1
4
5
7
6
d
a
b
c
8
9
10
11
f
e
R
0
2
1
3
6
5
4
a
7
e
R
b
g
f
c
d
g
Figura 1: Famı́lia de intervalos dada na entrada do Algoritmo 1 e a saı́da após a execução do algoritmo.
Lema 3.1 Se R é uma RINE, então existe uma representação por intervalos P , tal que cada
intervalo de R corresponde a um intervalo distinto de P e dois intervalos pertencentes a R
têm interseção não-vazia se, e somente se, os intervalos correspondentes em P têm interseção
não-vazia. Além disso, nenhum intervalo em P contém propriamente outro intervalo de P .
Demonstração: Considere uma RINE, R, e suponha que não existam dois ou mais intervalos
de R que terminem em um mesmo ponto. Neste caso, faça P = R. Logo, P é uma RINE. Pela
Definição 1.2 e, como não existem dois intervalos de P que terminam em um mesmo ponto, para
dois intervalos [a, b) e [c, d) em P , se a < c então b < d e, portanto, P é uma representação em
que nenhum intervalo contém propriamente outro.
Seja D o conjunto dos intervalos de R que não terminam no mesmo ponto que nenhum
outro intervalo de R. Inclua os intervalos pertencentes a D em P . Suponha que existam exatos
l > 1 intervalos em R \ D que terminam em um mesmo ponto a e seja L, o conjunto desses
intervalos. Considere que os intervalos de L estão em ordem crescente dos seus pontos iniciais:
l1 < l2 < l3 < . . . < ll . Para 1 ≤ i ≤ l, insira em P o intervalo [li , a − 1 + i/l). Se dois
intervalos não têm interseção em R, então seus correspondentes não terão interseção em P , pois
os intervalos em P são exatamente os mesmos ou menores. Se dois intervalos têm interseção nãovazia em R, então seus correspondentes têm interseção não-vazia em P , pois para cada intervalo
[li , a) ∈ L, tem-se li ≤ a − 1. Como a extremidade direita de qualquer intervalo pertencente a
L ∩ P é extritamente maior que a − 1, quaisquer dois intervalos com interseção entre os ponto
a − 1 e a na representação R correspondem a intervalos com interseção no ponto a − 1 em P .
O resultado que apresentamos torna válido o Teorema de Mertzios, que caracteriza os grafos
de intervalos próprios.
Teorema 3.2 [4] G é um grafo de intervalos próprios se, e somente se, G tem uma Representação por Intervalos Normal em Escada.
Referências
[1] D. G. Corneil, H. Kim, S. Natarajan, S. Olariu, and A. P Sorague. Simple linear time
recognition of unit interval graphs. Information Processing Letters, 55:99–104, 1995.
[2] C. M. H. Figueiredo, J. Meidanis, and C. P. de Mello. A linear-time algorithm for proper
interval graph recognition. Information Processing Letters, 56(3):179 – 184, 1995.
[3] F. Gardi. The roberts characterization of proper and unit interval graphs. Discrete Mathematics, 307:2906–2908, 2007.
[4] G. B. Mertzios. A matrix characterization of interval and proper interval graphs. Applied
Mathematics Letters, 21:332–337, 2008.
[5] F. S. Roberts. On the compatibility between a graph and a simple order. J. Comb. Theory,
11:28–38, 1971.
331