Questão - Sacramentinas

COLÉGIO NOSSA SENHORA DE FÁTIMA
ALUNO(A): ____________________________________________________________ Nº _____
PROF.: Murilo Gomes Santos
DISCIPLINA: Física
SÉRIE: 3ª – Ensino Médio
TURMA: ______
DATA: ____________________
ATIVIDADE AVALIATIVA 01
“Cristo morreu de braços abertos, para que
nós não ficássemos de braços fechados.”
Fique Atento:
 Sua avaliação consta de 20 questões e 02 desafios – Confira.
 Não é permitida a consulta de qualquer material e o uso de calculadora.
 Justifique com cálculos todas as suas respostas.
 Todas as questões objetivas possuem apenas uma única alternativa correta.
 As questões rasuradas ou sem justificativas serão automaticamente anuladas.
 Pontuação total de sua avaliação: 10,0.
Questão 01
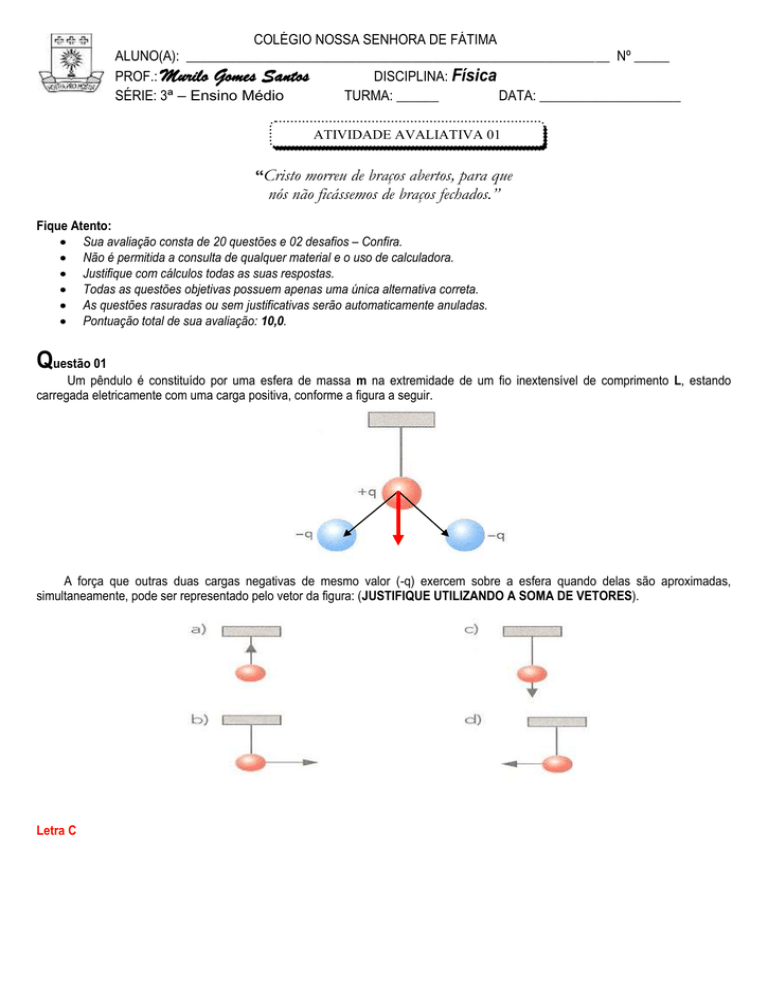
Um pêndulo é constituído por uma esfera de massa m na extremidade de um fio inextensível de comprimento L, estando
carregada eletricamente com uma carga positiva, conforme a figura a seguir.
A força que outras duas cargas negativas de mesmo valor (-q) exercem sobre a esfera quando delas são aproximadas,
simultaneamente, pode ser representado pelo vetor da figura: (JUSTIFIQUE UTILIZANDO A SOMA DE VETORES).
Letra C
Questão 02
A figura representa um eletroscópio de folhas. O eletroscópio pode indicar a presença de cargas elétricas e o sinal delas.
Considere o eletroscópio originalmente carregado positivamente. Aproximando-se dele um bastão carregado observa-se que as
folhas se fecham. É correto afirmar que:
a) O bastão tem carga negativa.
b) O bastão tem carga positiva.
c) O bastão tem cargas positivas e negativas não balanceadas.
d) Não é possível identificar a carga do bastão.
Questão 03
Três cargas elétricas puntiformes idênticas Q1, Q2 e Q3, são mantidas fixas em suas posições sobre uma linha reta, conforme
indica a figura a seguir.
Sabendo-se que o módulo da força elétrica exercida por Q1 sobre Q2 é de 4,0 x 10-5 N, qual é o módulo da força elétrica
resultante sobre Q2?
a)
b)
c)
d)
e)
4,0 x 10-5 N
8,0 x 10-5 N
1,2 x 10-4 N
1,6 x 10-4 N
2,0 x 10-4 N
Fr = F32 – F12
Como F12 = 4 x 10-5, com d = 10 cm, então F32 com d = 5 cm (metade de F12) será dada por:
F32 = F12 x 4 = 16 x 10-5 N
Fr = 16 x 10-5 – 4 x 10-5 = 12 x 10-5 N
Questão 04
Em cada um dos vértices de um triângulo equilátero, de 30 cm de lado, estão fixas as cargas Q 1 = −2𝜇𝐶 e Q2 = Q3 = +3𝜇𝐶,
todas puntiformes. Sabe-se que o meio em que estão imersas é o vácuo, em que a constante eletrostática é 9 . 10 9 N.m2/c2.
Considere √3 = 1,7, calcule a intensidade da força resultante que age em Q1, sabendo que Q2 e Q3 estão localizadas na base do
triângulo.

Q1
Como F21 = F31 = F, teremos:
Fr2 = F2 + F2 + 2.F.F.cos60°
Fr2 = 2F2 + F2
Fr2 = 3F2
Fr = √𝟑.F
Fr =
𝟏,𝟕.𝟗.𝟏𝟎𝟗 .𝟑.𝟏𝟎−𝟔 .𝟐.𝟏𝟎−𝟔
𝟗.𝟏𝟎−𝟐
Fr = 1,7 . 6.10-1
Fr = 1,7 . 0,6
Fr = 1,02 N
Questão 05
Duas cargas pontuais Q1 = Q e Q2 = 2Q, quando colocadas no vácuo, afastadas uma distância d, se repelem com uma força de
2N. Dobrando-se cada uma das cargas e reduzindo-se a um terço a distância entre elas, a nova força de repulsão, em N, é igual a:
a) 36
b) 72
c) 87
d) 94
e) 144
F = 2 . 2 . 2 . 9 = 72 N
Questão 06
Quatro cargas puntiformes de mesmo valor +q são colocadas no vértice de um quadrado de lado L. O vetor campo elétrico
resultante no centro do lado assinalado com um pontinho é:
Questão 07
O vetor campo elétrico gerado por uma carga puntiforme Q = -2,0 x 10-6 C, num ponto P, tem direção horizontal, sentido da
esquerda para direita e intensidade E = 2,0 x 105 N/C. O meio é o vácuo.
A posição da carga Q é:
a) 9,0 cm à direita de P.
b) 9,0 cm à esquerda de P.
c) 30 cm à direita de P.
d) 30 cm à esquerda de P.
e) 3,0 m à direita de P.
2.105 =
𝟗.𝟏𝟎𝟗 .𝟐.𝟏𝟎−𝟔
𝒅𝟐
d2 =
𝟗.𝟏𝟎𝟗
𝟏𝟎𝟓
d2 = 9.10-2
d = 0,3 m = 30 cm
Como a carga é negativa, o campo será de afastamento, ou seja:

Q
Questão 08
Duas cargas elétricas positivas puntiformes, A e B, iguais a 5.10-7 C e 8.10-6C, respectivamente, encontram-se em repouso no
vácuo, afastadas 5 m uma da outra. O vetor campo elétrico é nulo, num ponto P, situado entre as cargas, a uma distância de B igual
a:
𝑲. 𝟓. 𝟏𝟎−𝟕 𝒌. 𝟖. 𝟏𝟎−𝟔
=
𝒙𝟐
(𝟓 − 𝒙)𝟐
1,6.10-6x2 = (5 – x)2 . 10-7
16x2 = (5 – x)2
4x = 5 – x
5x = 5
X = 1m de A
Ou
4m de B
Questão 09
A figura mostra duas cargas elétricas de valores 4q e –q, fixas nos pontos c e e. Sabendo-se que os pontos são eqüidistantes e
separados por uma distância x, o campo elétrico resultante é nulo em
a) a
b) b
c) d
d) f
e) g
𝒌. 𝟒𝒒 𝒌. 𝒒
= 𝟐
𝒙𝟐
𝒚
4y2 = x2
X = 2y
Questão 10
Uma escala arbitrária adota os valores 5 e 365 para os pontos fixos fundamentais (ponto de fusão e ponto de ebulição,
respectivamente). Qual a indicação nessa escala que corresponde ao 0º F?
a) -49º
b) -59º
c) -69º
d) -79º
e) -89º
𝑻𝒄 − 𝟓
𝑻𝒇 − 𝟑𝟐
=
𝟑𝟔𝟓 − 𝟓 𝟐𝟏𝟐 − 𝟑𝟐
𝑻𝒄 − 𝟓 𝑻𝒇 − 𝟑𝟐
=
𝟑𝟔𝟎
𝟏𝟖𝟎
Tc – 5 = 2Tf – 64
Tf = 0° F
Tc – 5 = -64
Tc = -64 + 5
Tc = -59° C
Questão 11
O verão de 1994 foi particularmente quente nos Estados Unidos da América. A diferença ente a máxima temperatura do verão e
a mínima no inverno foram de 60º C. Qual o valor dessa diferença na escala Fahrenheit?
a) 108ºF
b) 60ºF
c) 140ºF
d) 33ºF
∆𝑻𝒇 = 𝟏, 𝟖. ∆𝑻𝒄
∆𝑻𝒇 = 𝟏, 𝟖. 𝟔𝟎
∆𝑻𝒇 = 𝟏𝟎𝟖 °𝑭
Questão 12
As indicações para o ponto de fusão e de ebulição da água sob pressão normal de dois termômetros, um na escala Celsius e
outro na escala Fahrenheit, distam 20 cm, conforme a figura.
A 5 cm do ponto de fusão do gelo, os termômetros registram temperaturas iguais a:
a)
b)
c)
d)
e)
25º C e 77º F
20º C e 40º F
20º C e 45º F
25º C e 45º F
25º C e 53º F
Como 5 cm corresponde a 0,25 de 20 cm, teremos:

Na escala Celsius:
100.0,25 = 25 °C

Na escala Fahrenheit:
180.0,25 = 45 °F
Questão 13
A figura a seguir mostra um diapasão vibrando na boca de um tubo, em cujo interior o nível de água vai descendo lentamente.
Verifica-se que, para determinados níveis de água, há um reforço de som e para outros não. O primeiro reforço de som ocorre quando
o nível de água se encontra a uma distância d = 15 cm da boca do tubo. Sendo de 300 m/s a velocidade do som no ar, determine:
a) a frequência da onda sonora emitida pelo diapasão.
b) o comprimento de onda do som.
c) à distância d’ do nível da água à boca do tubo, no instante em que ocorre o segundo reforço de som.
a) f =
𝒏.𝑽
𝟒𝑳
𝟏.𝟑𝟎𝟎
= 𝟒.𝟎,𝟏𝟓
f = 500 Hz
b) 𝝀 =
𝟐𝑳
𝒏
=
𝟒.𝟎,𝟏𝟓
𝟏
𝝀 = 𝟎, 𝟔 𝒎
c) N = 2
𝟓𝟎𝟎 =
𝟐. 𝟑𝟎𝟎
𝟒𝐋
20L = 6
L = 0,3 m ou 30 cm
Com 15 cm iniciais, teremos 45 cm.
Questão 14
Um observador parado ouve a sirene de uma ambulância aproximando-se dele, com frequência de 880 hz. Depois que passa, a
frequência ouvida é de 800 hz. Sendo de 350 m/s a velocidade do som no ar, calcule com que velocidade a ambulância passou pelo
observador.
𝟑𝟓𝟎+𝟎
I)
880 = 𝒇 (𝟑𝟓𝟎−𝑽𝑭)
𝟑𝟓𝟎+𝟎
II)
III)
800 = 𝒇 (𝟑𝟓𝟎+𝑽𝑭)
Igualando f de cada uma das equações, teremos:
𝟖𝟖𝟎
(𝟑𝟓𝟎−𝑽𝑭)
𝟑𝟓𝟎
(𝟑𝟓𝟎+𝑽𝑭)
𝟑𝟓𝟎
= 800.
3850 – 11VF = 3500 + 10VF
21VF = 350
VF = 16,67 m/s
Questão 15
Um automóvel se aproxima a uma velocidade de 30 m/s de uma sirene de fábrica que tem uma frequência de 510,0 Hz.
Sabendo-se que a velocidade do som no ar é de 340 m/s, pode-se afirmar que o motorista do veículo ouve, aparentemente, uma
frequência igual, em Hz, a
a) 603
b) 555
c) 526
d) 497
e) 436
𝟑𝟒𝟎+𝟑𝟎
𝟑𝟕𝟎
f’ = 510.( 𝟑𝟒𝟎+𝟎 ) = 𝟓𝟏𝟎. 𝟑𝟒𝟎 =
𝟏𝟖𝟖𝟕𝟎𝟎
𝟑𝟒𝟎
= 555Hz
Questão 16
Uma fonte sonora pontual emite um som com potência de 12,56 W, que se propaga uniformemente em todas as direções.
Considerando-se o limiar da audição – nível sonoro que pode danificar o ouvido humano – igual a 120 dB, a distância mínima com
que uma pessoa pode se aproximar da fonte, com segurança, deve estar em torno de
a) 100 cm
b) 90 cm
c) 80 cm
d) 70 cm
e) 60 cm
I)
120 dB = 1 w/m2
II)
I=
1=
𝑷𝒐𝒕
𝑨
𝟏𝟐,𝟓𝟔
𝟒.𝝅.𝑹𝟐
 4. 3,14 . R2 = 12,56  12,56 R2 = 12,56  R = 1m ou 100 cm.
Questão 17
Um tubo sonoro aberto de 50 cm de comprimento emite um som cuja freqüência é de 1360 Hz. Sendo o módulo da velocidade de
propagação do som no ar igual a 340m/s, o som emitido é o ________ harmônico.
a) segundo
b) terceiro
c) quarto
d) quinto
e) sexto
f=
𝒏.𝑽
𝟐𝑳
 1360 =
𝒏.𝟑𝟒𝟎

𝟐.𝟎,𝟓
340n = 1360  n = 4
Questão 18
A figura a seguir ilustra uma onda mecânica que se propaga numa velocidade 3,0 m/s e frequência:
a) 1,5 Hz.
b) 3,0 Hz.
c) 5,0 Hz.
d) 6,0 Hz.
e) 10,0 Hz.
I) 0,60 = 2.𝝀  𝝀 = 𝟎, 𝟑𝒎
II) V = 𝝀. 𝒇
3 = 0,3.f  f = 10 Hz
Questão 19
𝜋
4
Uma onda se propaga de acordo com a função y = 3.cos[ + 2𝜋(5𝑡 − 𝑥)], onde x e y são dados em cm e t em segundos.
Pede-se:
a) A amplitude e o comprimento de onda.
b) O período e a velocidade de propagação.
a) a = 3 cm
𝒙
2.𝝅. 𝒙 = 𝟐. 𝝅. 𝝀
𝝀 = 𝟏𝒄𝒎
b) 𝟐𝝅. 𝟓𝒕 = 𝟐𝝅.
𝒕
𝑻
5T = 1
T = 0,2 s
V = 1 . 5 = 5 cm/s
Questão 20
Qual deve ser aproximadamente, a massa do bloco P para que a freqüência fundamental do som emitido pela corda
inextensível, mostrada na figura a seguir, de densidade 10-3 kg/m e comprimento d = 50 cm, seja de 440 Hz?
Considere g = 10 m/s2.
a) 2 kg.
b) 5 kg.
c) 10 kg.
d) 20 kg.
e) 30 kg.
Desafio 01
Determine a intensidade, a direção e o sentido do campo elétrico no centro de um triângulo eqüilátero de lado igual a 3m, em
cujos vértices se encontram cargas Q1 = -2C, Q2 = -2C e Q3 = 4C, estando essas cargas no vácuo. (Q1 e Q2 estão localizadas na
base do triângulo).
Desafio 02
Seis cargas elétricas puntiformes se encontram no vácuo fixas nos vértices de um hexágono regular de lado L. As cargas têm
mesmo módulo, Q, e seus sinais estão indicados na figura.
Dados: L = 30 cm e Q = 5,0. 10-6 C.
No centro do hexágono, o módulo e o sentido do vetor campo elétrico resultante são, respectivamente:
a) 5,0 . 106 N/C, de E para B.
b) 5,0 . 106 N/C, de B para E.
c) 5,0 . 106 N/C, de A para D.
d) 1,0 . 107 N/C, de B para E.
e) 1,0 . 107 N/C, de E para B.