Parte II Máquinas Térmicas

Parte II Máquinas Térmicas
10. Generalidades e Revisão de Termodinâmica
10.1. Introdução
Desde os primórdios do seu aparecimento sobre a terra, o homem procurou utilizar o
fogo (calor) como componente indispensável à sua sobrevivência, seja para aquecer o corpo,
seja para preparar os alimentos ou realizar algum outro trabalho. Porém, a utilização de forma
ordenada da energia calorífica somente foi possível a partir do estabelecimento e divulgação
do 1o e 2o princípios da Termodinâmica, fato que ocorreu respectivamente em 1840 e 1850.
Graças a estes princípios, foi possível construir e estudar sistemas termodinâmicos que trocam
com o meio externo, de modo contínuo, as formas de energia calor e trabalho. Estes sistemas
são denominados Máquinas Térmicas.
A descoberta do petróleo permitiu um grande avanço no desenvolvimento das Máquinas
térmicas. Sendo o petróleo uma fonte não renovável de energia, o seu uso desenfreado, sem a
preocupação com a qualidade dos processos de transformação de energia, mas somente com a
quantidade, acabou levando a uma crise na década de 70. A partir daí, houve uma
preocupação com relação a qualidade da transformação; os ciclos das máquinas térmicas
voltaram a ser analisados e se buscaram novas fontes de energia, destacando-se a solar e a
biomassa com programas para a produção industrial de álcool e metano.
10.2. Classificação
Dentre as várias maneiras de se classificar as máquinas térmicas podemos citar:
a) Quanto ao trabalho
Máquinas Térmicas Motrizes: são as que transformam energia térmica em trabalho
mecânico. Se destinam a acionar outras máquinas.
Máquinas Térmicas Geratrizes ou Operatrizes: são aquelas que recebem trabalho
mecânico e o transforma em energia térmica. São acionadas por outras máquinas.
b) Quanto ao tipo de sistema onde ocorre a transformação de energia
Máquinas Térmicas a Pistão: nas quais a transferência de energia ocorre em um
sistema fechado.O elemento móvel é um pistão ou êmbolo, o qual pode ter movimento de
translação alternada ou movimento de rotação.
Máquinas Térmicas de Fluxo: nas quais a transferência de energia ocorre em um
sistema aberto. O elemento móvel é um disco ou tambor, que possui na extremidade um
sistema de pás, montadas de modo a formar canais por onde escoa o fluido de trabalho. O
movimento deste elemento é rotativo.
c) Quanto ao fluido de trabalho
Gás Neutro: ar, hélio e outros.
Vapores: vapor d'água e outros.
Gases de Combustão: resultantes da queima de combustível + oxigênio (ar).
A Tabela 10.1 mostra alguns exemplos de máquinas térmicas, seguindo estas
classificações.
Ao longo do curso serão vistos com mais detalhes, as turbinas a gás e a vapor, e os
motores Diesel e Otto.
Tab. 10.1. Classificação das Máquinas Térmicas
Gás Neutro
Máq. Térmicas
Motrizes (MTM)
Máq. Térmicas
Operatrizes
(MTO)
Máquinas a ar
quente
Compressores a
pistão
Turbinas
Aerodinâmicas
Ventiladores e
Turbocompresso
res
Vapores
Máq. Térmicas
Motrizes (MTM)
Máq. Térmicas
Operatrizes
(MTO)
Máquinas Térmicas à Pistão
Máquinas
a Compressores
vapor
para vapor
Máquinas Térmicas de Fluxo
Turbinas a vapor Turbocompresso
res a vapor
Gases de Combustão
Máq. Térmicas
Motrizes (MTM)
Motor
Otto,
Diesel, Wankel,
etc...
Turbinas a gás,
Turbohélice,
Turbojato, Pulso
jato,
Estatorreator,
Foguete
Máq. Térmicas
Operatrizes
(MTO)
__________
__________
10.3. Revisão da Termodinâmica
Neste item recordaremos alguns conceitos de Termodinâmica e faremos algumas
considerações úteis à compreensão do estudo das máquinas térmicas.
10.3.1. Definição de Termodinâmica
De maneira sucinta, Termodinâmica é definida como a ciência que trata do calor e do
trabalho, e daquelas propriedades das substâncias relacionadas ao calor e ao trabalho. É
baseada na observação experimental.
10.3.2. Estados de Equilíbrio, Ciclos e Processos Termodinâmicos
As transformações de energia que ocorrem numa máquina térmica se realizam por meio
de um fluido de trabalho que recebe, armazena e cede energia em diversas formas. Isto se
realiza devido as mudanças de estado sucessivas do fluido.
O fluido passar de um estado de equilíbrio a outro, através de uma série de estados de
equilíbrio intermediários, realiza um processo. Este pode ser aberto ou fechado, voltando
neste último caso o fluido ao estado inicial realizando-se assim um ciclo.
O estado pode ser identificado ou descrito por certas propriedades macroscópicas
observáveis (temperatura, pressão, densidade, etc...).
Quando um sistema está em equilíbrio com relação a todas as mudanças possíveis de
estado, dizemos que ele está em equilíbrio termodinâmico.
10.3.3. Propriedades Termodinâmicas
Uma propriedade pode ser definida como uma quantidade que depende do estado do
sistema e é independente do caminho pelo qual o sistema chegou ao estado considerado. As
propriedades termodinâmicas podem ser divididas em duas classes gerais:
Intensivas: propriedades que independem da massa. Ex: T e P
Extensivas: propriedades que dependem da massa. Ex: V, H e S.
Obs.: as propriedades extensivas específicas, isto é, propriedades reduzidas à unidade de
massa da substância, adquirem o caráter de propriedades intensivas.
Uma outra propriedade que pode ser definida como propriedade intensiva é o título (x)
que é uma propriedade que tem significado somente quando a substância está num estado
saturado, isto é, na pressão e na temperatura de saturação, que são respectivamente a pressão e
a temperatura na qual se dá a vaporização da substância para uma dada temperatura ou
pressão.
Se uma substância existe como líquido à temperatura e pressão de saturação é chamada
de líquido saturado.
Se a temperatura do líquido é mais baixa do que a temperatura de saturação para a
pressão existente, ele é chamado de líquido sub-resfriado (significando que a temperatura é
mais baixa que a temperatura de saturação para uma dada pressão) ou líquido comprimido
(significando ser a pressão maior do que a pressão de saturação para uma dada temperatura).
Se uma substância existe como vapor na temperatura e pressão de saturação, é chamada
vapor saturado.
Quando o vapor está a uma temperatura maior que a temperatura de saturação, é
chamado vapor superaquecido.
A temperatura e a pressão do vapor superaquecido, bem como do líquido comprimido
são propriedades independentes, pois uma pode variar enquanto a outra permanece constante.
Quando uma substância existe, parte líquida e parte vapor, na temperatura de saturação
o seu título é definido como a relação entre a massa de vapor e a massa total:
mv
x=
ml + m v
Neste caso, pressão e temperatura são propriedades dependentes, necessitando-se do
título para se definir um estado, que é caracterizado, na ausência de forças externas, por duas
propriedades intensivas independentes.
O estado de uma substância pura pode ser determinado, na ausência de forças externas,
por apenas duas propriedades intensivas independentes.
Assim, com a substância definida num dado estado, todas as outras propriedades
termodinâmicas assumirão valores particulares, calculáveis através de relações a partir das
duas propriedades originalmente especificadas.
Essas relações termodinâmicas podem ser representadas em diagramas bidimensionais,
em coordenadas retangulares, com uma das propriedades de estado tomada na abscissa e outra
na ordenada.
Esses diagramas de estado (ou de propriedades) são utilizados não só no recurso de
representação das demais propriedades, bem como na visualização das mudanças de estado
que ocorrem nos diversos processos. Os diagramas usuais são:
•
Temperatura x Entropia específica (T x s)
•
Temperatura x Entalpia específica (T x h)
•
Pressão x Volume específico (P x ν)
•
Entalpia esp. x Entropia esp. (h x s) - Diagrama de Mollier.
Por sua importância nos estudos dos ciclos de potências veremos com mais detalhes o
diagrama T x s , que tem a forma mostrada na figura 10.1.
Figura 10.1: Diagrama temperatura - entropia para o vapor d'água.
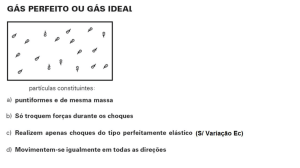
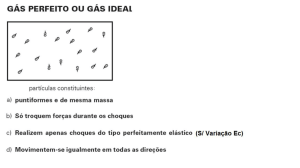
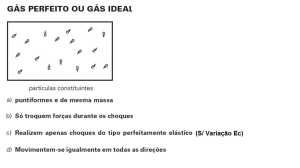
10.3.3.1. Equação de estado do Gás Perfeito e do gás real
Um corpo pode encontrar-se em 3 estados físicos: sólido, líquido e gasoso. Estes
estados se caracterizam precisamente pela importância das forças de coesão entre as
moléculas e o volume molecular:
- Estado Sólido: as moléculas estão muito próximas, não tem movimento de
translação e as forças de atração ou repulsão entre elas são máximas.
- Estado Líquido: a distância entre as moléculas aumenta com relação ao estado
sólido, mas ainda é pequena. Elas se movem com velocidade de translação e as forças de
coesão moleculares são menores.
- Estado Gasoso: aumenta extraordinariamente o volume ocupado pela substância,
com o aumento da distância entre as moléculas e diminuem consideravelmente as forças de
coesão.
Gás Perfeito: é aquele em que podemos desprezar tanto o volume molecular como a
força de atração entre as moléculas. É uma extrapolação das tendências que mostram os gases
reais a baixas pressões e elevados volumes específicos.
Para um processo entre os estados 1 e 2, podemos escrever:
P1 × ν1 P2 × ν 2
=
T1
T2
que é a equação geral de um gás perfeito.
A temperatura constante o volume específico de um gás perfeito varia em razão inversa
da pressão absoluta:
P1 ν2
=
(Lei de Boyle-Mariotte).
P2 ν1
A pressão constante o volume específico de um gás perfeito varia diretamente com a
temperatura absoluta:
T1 ν1
=
(1a Lei de Gay-Lussac).
T2 ν 2
A volume constante a pressão absoluta varia diretamente com a temperatura absoluta:
P1 T1 P1 T1
=
=
(2a Lei de Gay-Lussac).
P2 T2 P2 T2
P.ν
Como os estados 1 e 2 são arbitrários, podemos escrever:
= R = cte que depende da
T
natureza do gás e que pode ser determinado experimentalmente.
Assim, podemos escrever:
Pv = RT ou PV = nR T
que é a equação de estados para gases perfeitos ou Eq. de Clapeyron.
Experiências realizadas com gases reais em grandes intervalos de pressões e
temperaturas demonstram que eles se comportam um pouco diferente dos gases perfeitos.
Assim, para definir uma equação para os gases reais é necessário introduzir um fator na
equação dos gases perfeitos que é denominado fator de compressibilidade (Z):
Pv = ZRT
Note que:
- para um gás perfeito Z = 1
- o desvio de Z em relação a unidade é uma medida do desvio da relação real
comparada à equação de estado dos gases perfeitos
10.3.4. Energias
10.3.4.1 - Energias Armazenadas
a) ENERGIA POTENCIAL OU GRAVITACIONAL OU DE POSIÇÃO:
A energia potencial, ou gravitacional ou energia de posição depende da altura do centro
de gravidade do corpo com relação a um plano horizontal de referência.
 Ep = m ⋅ g ⋅ h [ J ]
Ep = m ⋅ g ⋅ h Ep = 
[ J / Kg ]
ep = g ⋅ h
b) ENERGIA CINÉTICA:
A energia cinética é devida ao movimento de translação do centro de gravidade do
corpo e da rotação.
 Ec = 1 2 ⋅ m ⋅ v 2 [ J ]

2
J Kg
ec = 1 2 ⋅ v
c) ENERGIA INTERNA:
É a energia das moléculas e átomos constituída por:
- Ec. de translação das moléculas;
- Ec. de rotação das moléculas;
- Ec. vibratória dos átomos nas moléculas;
- Ep. das moléculas devida a força de atração entre as mesmas.
u = f (ν , T )
u = f 1 ( p, ν )

⇒
f ( p,ν , T ) = 0 eq. estado 
u = f 2 ( p, T )
l
[
]
10.3.4.2. Energias de Trânsito
Representa a energia que atravessa a fronteira de um sistema na forma de trabalho ou
calor. São funções de linha (diferenciais inexatas).
a) TRABALHO:
Um sistema realiza trabalho se o único efeito sobre o meio (tudo o que é externo ao
sistema) puder ser equivalente ao levantamento de um peso, como mostra a figura 10.2.
Figura 10.2: Exemplo de um trabalho realizado na fronteira de um sistema.
Figura 10.3: Exemplo de trabalho atravessando a fronteira de um sistema devido ao fluxo de
uma corrente elétrica através da mesma.
O trabalho é usualmente definido como uma força F agindo através de um deslocamento
dx na direção desta força:
2
W = ∫ F ⋅ dx
1
ou de outro modo, como mostra a figura 10.4:
2
2
F = p ⋅ A⇒ 1W2 = ∫ p ⋅ 1
A2
⋅3
dx⇒ 1W2 = ∫ p ⋅ dV
1
1
dV
Figura 10.4: Uso do diagrama pressão-volume para mostrar o trabalho realizado devido ao
movimento de fronteira de um sistema num processo quase-estático.
Portanto, o trabalho nada mais é do que a área sob a curva no gráfico PxV e como se
verifica não é função somente dos estados inicial e final, mas também depende do caminho
que se percorre para ir de um estado ao outro.
Obs: não existe W2 − W1 e sim 1W2 .
Convenção:
W realizado pelo sistema: +
W realizado sobre o sistema: b) CALOR:
É definido como sendo a forma de energia transferida através da fronteira de um
sistema, numa dada temperatura, a um outro sistema (ou meio) numa temperatura inferior, em
virtude da diferença de temperatura entre os dois sistemas. Que pode ser transferida por
condução, convecção, ou radiação.
Tal como o trabalho o calor transferido quando um sistema sofre uma mudança, do
estado 1 para o estado2, depende do caminho que o sistema percorre durante a mudança de
estado.
2
1
Q2 = ∫ ∂Q
1
Num processo em que não há troca de calor, é chamado processo adiabático.
Convenção:
Q transferido para o sistema: +
Q transferido de um sistema: -
10.3.4.3. Entalpia
É uma propriedade que por definição é a soma da energia interna e do trabalho de
escoamento:
h = u + p⋅ν
h = f1 ( p, T)
h = f2 ( p, ν)
H = U + p⋅V
10.3.4.4. Calor Específico
É a quantidade de calor que é preciso fornecer a uma unidade de massa de uma
substância para elevar a sua temperatura, em um determinado processo, em 1 grau.
c = f 1 (T , P)
cv = f 2 (T , P) (calor específico a volume cons tan te)
c p = f 3 (T , P) (calor específico a pressão cons tan te)
 ∂u 
cv =  
 ∂T  v
 ∂h 
cp =  
 ∂T  p
10.3.4.5 - Outras Formas de Energia
Além das enunciadas existem outras formas de energia, a saber, energia elétrica, energia
química, energia eletromagnética, energia acústica, energia nuclear, energia de fricção, etc...
10.3.5 - Sistemas Termodinâmicos
Sistema termodinâmico é uma região do espaço ou uma porção de fluido limitada por
fronteiras reais ou imaginárias que o separam da vizinhança.
10.3.5.1 Sistemas Fechados e Abertos
a) SISTEMA FECHADO:
É aquele em que o fluxo de massa do exterior ao interior ou do interior para o exterior
do sistema é nulo. Tem massa e identidade fixas.
O fluxo de energia em forma de calor ou trabalho pode ou não ser nulo, mas nos
sistemas fechados de nosso interesse não o é.
Se o fluxo de calor for nulo nas fronteiras sistema ele é isolado termicamente.
Se o fluxo de calor e o trabalho são nulos o sistema é isolado.
b) SISTEMA ABERTO:
É aquele em que existe fluxo de massa do interior ao exterior ou do exterior ao interior
do sistema. É também conhecido como volume de controle (V.C.).
10.3.5.2. Sistemas Estáticos e Dinâmicos
a) SISTEMA ESTÁTICO:
É aquele em que só tem lugar processos estáticos. Neles só pode variar a energia interna
do sistema. O fluxo e a variação de energia cinética ou potencial são nulos.
b) SISTEMAS DINÂMICOS:
É aquele em que o fluido (ou substância) percorre com variação não só da energia
interna como também da energia potencial e cinética.
Os sistemas dinâmicos podem ser abertos ou fechados. Os abertos são mais importantes
nos estudos das máquinas térmicas.
10.3.5.3 Sistemas Dinâmicos Abertos em Regime Permanente
É o sistema mais freqüente nos estudos da máquinas térmicas Suas características são:
- o fluxo mássico em cada seção transversal ao fluxo é constante e não há acumulação nem
diminuição de massa em nenhum ponto do sistema;
- não há incremento ou diminuição de energia em nenhum ponto do sistema; o fluxo de calor
e trabalho nas fronteiras são constantes,
- todas as propriedades termodinâmicas (p,,T,,etc...) permanecem constantes ao longo do
tempo em qualquer ponto do sistema.
Ex: Turbina a vapor, passado o período da colocação em marcha
10.3.6. Processos Termodinâmicos
10.3.6.1. Processos Abertos e Fechados (Ciclos)
Existem 4 processos elementares em que se mantém constante um parâmetro
termodinâmico e que são de suma importância no estudo das máquinas térmicas:
- processo isobárico (p = cte)
- processo isocórico (V = cte)
- processo isotérmico (T = cte)
- processo adiabático - isoentrópico (dQ = 0 e s = cte) importantíssimo no estudo das
máquinas térmicas pois representa o trabalho ideal.
A figuras 10.5 e 10.6 a seguir, mostram estes processos nos planos PxV, Txs e hxs.
Figura 10.5: Os quatro processos elementares representados nos planos pv, Ts e hs: (a)
processo isobárico; (b) processo isocórico.
Figura 10.6: (c) processo isotérmico; (d) processo adiabático-isoentrópico.
Outros processos:
- processo adiabático (dQ = 0)
- processo isoentrópico (s = cte)
- processo isoentálpico (h = cte)
- processo politrópico (processo que obedece a eq.: P ⋅ ν n = cte ).
Obs: Os 4 processos enunciados inicialmente podem ser considerados como casos
particulares do processo politrópico; a saber:
- n = 0: processo isobárico.
- n = 1: processo isotérmico.
- n = γ = Cp Cv ⇒ processo adiabático.-isoentrópico.
- n = ∞ processo isocórico.
Figura 10.7: Processo politrópicos diversos: (a) no plano pv; (b) no plano Ts. O ponto 1 se
considera na origem em todos os processos politrópicos, n pode tomar qualquer valor de -∞ à
+∞.
A figura 10.7 mostra estes processos nos planos Pv e Ts.
Existem dois outros tipos de processos:
- processo de expansão: é aquele em que o volume específico do gás aumenta. Normalmente a
pressão diminui, mas também pode permanecer constante ou aumentar.
- processo de compressão: é aquele em que o volume específico do gás diminui. Normalmente
a pressão aumenta, mas também pode permanecer constante ou diminuir.
A figura apresentada a seguir, mostra esses processos.
Figura 10.8: (a) Tipos diversos de processos de expansão; (b) Tipos diversos de processos de
compressão.
10.3.6.2. Processos Reversíveis e Irreversíveis
Um processo se chama reversível quando, uma vez realizado, o sistema pode retornar ao
seu estado inicial sem mudança alguma no meio exterior, de maneira que o processo pode se
dar em ambas as direções sem mudanças.
Para exemplificar, consideremos a seguinte figura:
Figura 10.9: Explicação do conceito de processo reversível.
Inicialmente o gás se encontra no estado 1. A fonte de calor fornece ou recebe calor do
gás dependendo do caso. O acumulador de energia mecânica absorve energia do gás quando o
volante se acelera e cede energia ao gás quando o volante desacelera. O gás se expansiona
segundo a trajetória 1-2 passando por uma série de estados de equilíbrio.
Nesta expansão o gás realiza um trabalho que se acumula em forma de energia cinética
no volante.
Num caso ideal, realizado o processo de expansão, o gás poderia voltar em sentido
contrário segundo a mesma trajetória 2-1, para o qual a energia cinética acumulada no volante
se inverteria em trabalho de compressão do gás, o qual ao se aquecer devolveria exatamente a
mesma quantidade de calor a fonte que a mesma havia cedido no processo 1-2.
Na prática, todos os processos reais são irreversíveis. No caso apresentado
anteriormente, na situação real, a compressão não seguiria o trajeto 2-1, pois tem o efeito do
atrito e da troca de calor com o meio.
Os processos reais lentos se aproximam dos reversíveis, porque neles a pressão, que se
propaga rapidamente, é praticamente a mesma em cada instante.
Os processos reversíveis são os que apresentam maior rendimento. O processo real tem
tanto maior rendimento quanto mais se aproxima do processo ideal reversível.
10.3.7 - Algumas Características e Processos dos Gases Perfeitos
10.3.7.1 - Calor Específico
Para os Gases Perfeitos o calor específico não depende da pressão só da temperatura
(c=f(t)).
dQ
⇒ dq = c ⋅ dT ⇒ Q = ∫ m ⋅ c ⋅ dT
dT
 ∂u 
cv =  
 ∂T 
 ∂h 
cp =  
 ∂T 
Obs: Cp é sempre maior que Cv porque para uma mesma elevação de temperatura no
processo isobárico se necessita mais calor, a saber, além do necessário para a elevação da
energia interna, o necessário para realizar trabalho
c=
10.3.7.2. Equação de Mayer
Uma equação muito usada na termodinâmica é:
cp
γ =
⟩1
cv
que é função da temperatura e da pressão.
Sabemos ainda que:
h = u + p ⋅ ν ⇒ dh = du + d ( p ⋅ ν )
para G. P. ⇒ p ⋅ ν = R ⋅ T
( R = cte)
Assim, temos:
dh = du + R ⋅ dT . Mas:
du ≅ cv ⋅ dT e dh ≅ c p ⋅ dT
c p ⋅ dT = cv ⋅ dT + R ⋅ dT . Daí R = c p − c v
resultando
(Equação de Mayer). Portanto, pode-se deduzir
outras equações muito usadas em Termodinâmica:
R
cv =
γ −1
γ ⋅R
cp =
γ −1
10.3.7.3. Processos Adiabáticos Reversíveis dos Gases Perfeitos.
O processo Adiabático-Reversível, que denominamos processo AdiabáticoIsoentrópico, depois de definir entropia, é fundamental no estudo das máquinas térmicas;
sendo o processo ideal de expansão nas turbinas a vapor e T.G. e processo ideal de
compressão nos T.C..
Em todo o processo reversível: ∂q = ∂u + p ⋅ ∂ν . Tratando-se de um gás perfeito e
processo adiabático podemos escrever:
−p
0 = cv ⋅ dT + p ⋅ dν ⇒ dT =
⋅ dν
cv
Por outro lado: p ⋅ ν = R ⋅ T . Diferenciando: p ⋅ dν + ν ⋅ dp = R ⋅ dT . Daí
p ⋅ dν + ν ⋅ dp
dT =
R
Portanto, igualando as duas equações para T, temos:
− p ⋅ dν p ⋅ dν + ν ⋅ dp
=
cv
R
c
Mas R = c p − c v e γ = p
cv
Simplificando e arranjando a equação acima, temos:
dp
dv
+γ ⋅
=0
p
v
com γ = cte, integrando, temos:
ln p + γ ⋅ ln ν = ln cte
ln p ⋅ νγ = ln cte
Assim: p ⋅ νγ = cte eq. processo adiabático-reversível. Que entre dois estados 1 e 2,
quaisquer pode ser escrita como:
γ
p1  ν2 
= 
p2  ν1 
A partir destas equações e da eq. de estado são deduzidas outras equações de grande
utilidade:
T1  ν2 
= 
T2  ν1 
γ −1
γ
p
=  1
 p2 
γ −1
γ
p1  T1  γ −1
= 
p2  T2 
10.3.7.4. Calor e Trabalho nas Transformações Isotérmicas Reversíveis dos Gases
Perfeitos
Em toda transformação reversível: dq = du + p ⋅ dν
u = f(t) para gás perfeito ⇒ du = 0 para T = constante.
Portanto, resulta: q =
∫ p ⋅ dv
p1 ⋅ ν1
ν
Substituindo na equação acima e integrando entre os limites 1 e 2 (começo e fim do
processo), temos:
ν 
ν 
q 2 = p1 ⋅ ν1 ⋅ ln 2  = R ⋅ T1 ⋅ ln 2 
 ν1 
 ν1 
ν 
dν
W = ∫ p ⋅ dν = cte ⋅ ∫
= p1 ⋅ ν1 ln 2 
ν
 ν1 
ν 
p 
W = p1 ⋅ ν1 ⋅ ln 2  = R ⋅ T1 ⋅ ln 2 
 ν1 
 p1 
Por outro lado: p =
10.3.8. A Lei Zero da Termodinâmica
Enunciado: "Quando dois corpos têm igualdade de temperatura com um terceiro corpo,
eles terão igualdade de temperatura entre si".
Essa lei constitui realmente a base da medida de temperatura, porque podemos colocar
número no termômetro de mercúrio e sempre que um corpo tiver igualdade de temperatura
com o termômetro poderemos dizer que o corpo tem a temperatura lida no termômetro
10.3.9. A 1a Lei da Termodinâmica
A 1a Lei da Termodinâmica é a aplicação à Termodinâmica de uma Lei de natureza
universal que é a Lei da conservação da energia. Esta Lei se enuncia assim:
“A energia do universo não se cria e nem se destrói, só se transforma de uma forma em
outra ou se comunica de um corpo ao outro”.
Em particular, o calor pode se transformar em trabalho mecânico e este em calor,
existindo uma equivalência exata entre as quantidades que participam da transformação.
1o Enunciado da 1a Lei da Termodinâmica
"O calor nada mais é do que uma forma de energia essencialmente equivalente ao
trabalho mecânico".
Equivalente Mecânico do Calor: 1 Kcal = 4186,8 J
2o Enunciado da 1a Lei da Termodinâmica
“Em todo sistema (aberto ou fechado, estático ou dinâmico, em regime permanente ou
transitório):
Energia que entra = incremento (positivo ou negativo) de energia armazenada no
sistema + Energia que sai.
ou
Energia final armazenada = energia inicial armazenada + (Energia que entra - Energia que
sai)”.
3o Enunciado da 1a Lei da Termodinâmica
“É impossível construir uma máquina que restitua continua e indefinidamente mais
energia que a absorvida (moto perpétuo de primeira espécie)”.
Formulações da 1a Lei da Termodinâmica:
a) SISTEMAS ESTÁTICOS
Nestes sistemas não há trabalho de fluxo, nem se armazena energia cinética e potencial.
Assim:
Q = ( U2 − U1 ) + W
(Supondo que não exista transformação química).
Se o processo é reversível e se trata de um sistema fechado, temos:
q = ∆u + ∫ p ⋅ dν
ou
dq = du + dw
b) SISTEMAS FECHADOS:
Nestes sistemas se pode armazenar não só energia interna como também energia
cinética e potencial.
Assim:
Q = ( E 2 − E1 ) + W
ou
dQ = dE + dW
onde:
E = Energia Interna + Energia Cinética. + Energia Potencial.
c) SITEMAS DINÂMICOS ABERTOS EM R.P.
Em um sistema fechado o estado final do processo está separado temporariamente do
estado inicial. Ex: Compressor de Embolo (quando a válvula de admissão está fechada, o gás
no interior do cilindro passa sucessivamente no tempo por uma série de estados intermediários
até o estado final da compressão).
Em um sistema aberto todos os processos (inicial, intermediário e final) ocorrem
simultaneamente no tempo, mas localmente em posições diferentes.
Ex: Turbina a vapor (um observador que se movesse com a corrente passaria
sucessivamente pela entrada da máquina (estado inicial), pelo rotor (estado intermediário) e
por fim pela saída da máquina (estado final).
O esquema apresentada a seguir representa um sistema aberto qualquer (por exemplo:
turbinas a vapor, caldeira, trocador de calor, etc,...).
Figura 10.10 Esquema energético de um sistema.
Na seção 1 entra massa e energia e na seção 2 sai.
Esta figura representa o caso geral onde existe todas as formas de energia (interna,
cinética, potencial, trabalho, calor). Em R.P. não se armazena massa e nem energia no
sistema. Como não há acumulação de energia, temos:
Energia que entra no sist. = Energia que sai do sist.
Portanto,
U1 + p1 ⋅ V1 + EC1 + EP1 + Q = U2 + p 2 ⋅ V2 + EC2 + EP2 + W
ou
Q = ∆U + ∆( p ⋅ V ) + ∆EC + ∆Ep + W
Levando-se em conta que a massa que entra no sistema é igual a que sai em R.P.
podemos escrever a eq. acima em termos específicos (por unidade de massa):
q = ∆u + ∆( p ⋅ v ) + ∆z ⋅ g + ∆( c 2 2) + w
dq = du + d ( p ⋅ ν ) + d ( z ⋅ g ) + d ( c 2 2) + dw
14244
3
dh
dq = dh + d ( z ⋅ g ) + d ( c 2 2) + dw
q = ∆h + ∆( z ⋅ g ) + ∆( c 2 2) + w
Observações:
a) Nos sistemas analisados em máquinas térmicas os incrementos de energia potencial são
em geral desprezíveis em comparação com os outros termos (gz = 0).
b) Ao se estudar máquina e aparatos que não são especificamente trocadores de calor (ex:
turbina, bomba, etc...) considera-se que neles se realiza um proc. adiabático, desprezandose o calor por condução e radiação (Q = 0).
c) Ao aplicar a equação geral para sistema aberto em R.P. a uma máquina ou sistema
específico pode acontecer que um ou vários termos são nulos ou desprezíveis, simplificando
assim a equação.
Ex1: Turbina a vapor ou Turbina a gás.
A energia cinética de entrada e saída são quase iguais: a variação da EC é desprezada

 ∆c 2

≅ 0 .
 2

Juntamente com as aproximações feitas em a) e b), resulta:
w = − ∆h ⇒ w = h1 − h 2
Ex2: Bocal
Um bocal não absorve e nem restitui trabalho (W=0), nem é um trocador de calor
(Q=0), assim:
∆(c 2 2) = − ∆h
 ∆c 2 c22 
Ainda, a energia na entrada é desprezível com relação a da saída 
≅  . Assim,
2
 2
c22
= − ∆h ⇒ c2 = 2 ⋅ (h1 − h2 )
2
d) No processo de estrangulamento (processo em R.P. através de uma restrição no escoamento
resultando numa queda de pressão), ex: válvula, não há trabalho nem variação de energia
potencial e fazendo a hipótese que não há transferência de calor, temos:
 c2 
c2
c2
h1 + 1 = h2 + 2 ⇒ − ∆h = ∆  
2
2
 2
Se o fluido for um gás, o volume específico sempre cresce neste processo e, portanto, se
o conduto tiver seção transversal cte, a energia cinética crescerá.
Em muitos casos, no entanto, esse acréscimo é pequeno (ou talvez a seção transversal
do conduto de saída seja maior que a de entrada) e podemos dizer com boa precisão que as
entalpias inicial e final são iguais.
Portanto, h1 = h 2 (processo isoentálpico).
10.3.10. Relações entre as integrais de p e v.
10.3.10.1. A integral
2
∫ p ⋅ ∂ν
1
Para todo processo estático reversível:
q − ∆u = ∫ p ⋅ dν
Para todo processo dinâmico:
( )
2
q − ∆u = ∆( p ⋅ ν ) + ∆ c 2 + ∆( g ⋅ z ) + w
Se os estados inicial e final são iguais, o calor q só depende da curva do processo (se é
isobárico, isocórico, etc...), não de se o processo é estático ou dinâmico, portanto para a
mesma curva de processo q é igual em ambas as equações. A energia interna, u, tenderá
também ao mesmo valor no processo estático que no processo dinâmico, porque por ser
função de ponto não depende mais do estado inicial e final.
(
∫
)
Portanto p ⋅ dν = ∆ ( p ⋅ν ) + ∆ c 2 2 + ∆ ( g ⋅ z ) + w
∫ p ⋅ dv = w
( processo. dinâmico)
(processo. estático)
No entanto, para qualquer processo estático ou dinâmico reversível:
q − ∆u =
∫ p ⋅ dv
ou
( 1a Lei para todo processo reversível )
dq = du + p ⋅ dv
2
10.3.10.2. A integral − ∫1 v ⋅ dp
a) para qualquer processo reversível (estático ou dinâmico)
dh = du + d(p⋅v) = du + v⋅dp +p⋅dv
dq = du + p⋅dv
⇒ dh = dq + v⋅dp ⇒ - v⋅dp = dq - dh
2
∴ − ∫ v ⋅ dp = q − ∆ h
1
b) para processo dinâmico reversível.
( )
2
dq = du + p⋅dv + v⋅dp + d c 2 +d(g⋅z) + dw
dq = du + p⋅dv
d(g⋅z) = 0
2
Assim, - v⋅dp = d c 2 + dw
( )
∫
2
( 2 )+ w
− v ⋅ dp = ∆ c
1
( )
2
∫
2
2
Se ∆ c 2 ≅ 0 ⇒ − v ⋅ dp = w
1
2
10.3.10.3. Relação entre
− ∫ v. dp e
1
2
∫ p. dv
1
Figura 10.11 Relação entre − ∫ v. dp e
∫ p. dv
2
w=
∫ p.dv
(proc. estático)
1
2
 c2 
w = − v.dp (proc. dinâmico com ∆   ≅ 0 )
 2
∫
1
Quando se trata de um gás perfeito e de um processo adiabático reversível, além de
c 
∆   ≅ 0 , temos :
 2
dq = du + p.dv
com dq = 0
du = cv . dt
2
2
Resulta : p.dv = - cv.dt. Integrando , temos :
∫ p. dv = c
v
. (T1 − T2 )
1
2
se Cv = cte ⇒ ∫ p. dv =
1
R
1
(T1 − T2 ) =
( p . v − p2 . v2 )
γ −1
γ −1 1 1
 c2 
Por outro lado, com ∆   ≅ 0 , temos :
 2
2
∫
w = − v.dp
1
Assim,
2
∫
− vdp =
1
2
∫ pdv + p v − p v
1 1
1
2 2
2
∫
− v.dp =
1
γ
γ −1
2
∫
( p1.v1 − p2 .v2 ) = γ . p.dv
1
2
Assim, temos que : −
∫ v. dp
1
2
=γ
∫ p. dv
1
10.3.10.4. Integrais cíclicas
A figura a seguir representa um ciclo composto de 3 processos elementares :
Figura 10.12 − ∫ p. dv = − ∫ v. dp
1 → 2 ⇒ isobárico
2 → 3 ⇒ adiabático- reversível
3 → 1 ⇒ isotérmico
Neste ciclo, adicionou-se calor ao fluído a temperatura constante (Q 31 ⟩ 0) e retira-se
calor a pressão constante ( Q12 ⟨ 0) ,sendo Q 2 3 = 0 .
 c2 
Para o ciclo : ∆u = ∆   = ∆ ( g. z ) = ∆ ( p. v ) = 0
 2
Assim : ∫ dq = ∫ dw ⇒ − ∫ v. dp =
∫ p.dv
Note-se a diferença entre o ciclo percorrido no sentido horário (1-2-3-1) e no sentido
anti-horário (3-2-1-3) :
• no sentido horário :
3
a) no sistema estático o trabalho de expansão w31 =
∫ p. dv ⟩0 é maior que o trabalho de
1
compressão
w12 =
3
Assim o trabalho total
2
3
1
2
∫ p. dv + ∫ p.dv⟨0 .
∫ dw⟩0
1
b) no sistema dinâmico o trabalho de expansão w13 = − ∫ v. dp⟩0 é maior que o trabalho
3
de compressão, que é nulo no processo 1 → 2 e negativo no processo 2 → 3 .
Assim o trabalho total : ∫ dw⟩0
• no sentido anti-horário :
Se comprova exatamente o contrário, ou seja que :
∫ dw⟨0
tanto no sistema estático
quanto no dinâmico.
Obs.: w e q são característica do processo ( funções de linha que dependem do caminho de
integração).
p,ν,u,t,h e s são característica de estado ou propriedades termodinâmicas (função do
ponto).
10.3.11. Segunda lei da termodinâmica
10.3.11.1. Introdução
Historicamente a primeira lei da termodinâmica constitui uma particularização aos
processos térmicos de uma lei universal, ao passo que a segunda lei foi descoberta primeiro
em conexão com os processos térmicos, generalizando-se depois a todos os processos naturais
e enunciando-se como uma lei universal de toda a natureza.
A primeira lei serve para analisar as transformações energéticas qualitativas e
quantitativamente. A segunda lei serve qualitativa e quantitativamente para analisar os
processos termodinâmicos, assim como para estudar o rendimento das máquinas térmicas.
A primeira lei estabelece a equivalência de todas as transformações energéticas. A
segunda lei analisa a direção destas transformações.
10.3.11.2. Enunciados da Segunda Lei
Há muitos enunciados da segunda lei, os quais mutuamente se completam. Entre eles
podemos citar :
a) Primeiro Enunciado (Kelvin - Plank)
"Não é possível construir um motor periódico que realize trabalho mecânico as custas
somente da refrigeração de uma fonte de calor."
ou
"É impossível construir um dispositivo que opere num ciclo termodinâmico e que não
produza outros efeitos além da realização de trabalho e troca de calores com um único
reservatório térmico."
ou
"É impossível construir um máquina térmica que opere num ciclo, que receba uma dada
quantidade de calor de um corpo à alta temperatura e produza igual quantidade de trabalho (
⇒ η < 100%)."
b) Segundo Enunciado (Clausius)
"O calor não pode passar espontaneamente de um corpo a outro, cuja temperatura seja
superior a do primeiro."
ou
"É impossível construir um dispositivo que opere num ciclo termodinâmico e que não
produza outro efeitos além da passagem de calor de um corpo frio para um corpo quente."
ou
"É impossível construir um refrigerador que opere sem receber trabalho. (⇒ β < ∞)"
c) Terceiro Enunciado
"É impossível construir um moto-perpétuo de segunda espécie."
ou
Um moto perpétuo de primeira espécie criaria trabalho do nada ou criaria massa e
energia violando, portanto a primeira lei, como já foi visto.
ou
Um moto-perpétuo de segunda espécie não infrigiria a primeira lei mas sim a segunda
lei.
d) Quarto Enunciado
"Os processos espontâneos na natureza não são reversíveis."
ou
Os processos da natureza se classificam em espontâneos e não espontâneos segundo se
para realizá-lo se requererá ou não um processo adicional.
Este enunciado nada mais é que uma generalização do enunciado de Clausius.
Observações :
- Todos os enunciados são negativos ( ⇒ é impossível demonstrar )
- A segunda lei baseia-se na evidência experimental.
- Todos os enunciados são equivalentes.
10.3.11.3. Ciclo de Carnot
É o ciclo reversível de maior rendimento que pode operar entre dois reservatórios de
temperatura constante.
Independentemente da substância de trabalho este ciclo apresenta sempre os mesmos 4
processos básicos:
1) Um processo isotérmico reversível, no qual calor é transferido de ou para ou
reservatório quente.
2) Um processo adiabático reversível, no qual a temperatura do fluido de trabalho
passa daquela do reservatório quente àquela do reservatório frio.
3) Um processo isotérmico reversível, no qual o calor é transferido para ou do
reservatório frio.
4) Um processo adiabático reversível, no qual a temperatura do fluido de trabalho
passa daquela do reservatório frio aquela do reservatório quente.
A figura mostra um exemplo de uma máquina térmica que opera num ciclo de Carnot.
Figura 10.13 Exemplo de uma máquina térmica que opera num ciclo de Carnot.
Note que o ciclo de Carnot é reversível, assim todos os processos podem ser invertidos
(ver linhas tracejadas e entre parênteses) transformando a máquina térmica num refrigerador.
Deve-se salientar que o ciclo de Carnot pode ser executado de vários modos diferentes.
Várias substâncias de trabalho podem ser usadas e existem também diversos arranjos
possíveis das máquinas.
Figura 10.14 Exemplo de um sistema gasoso operando num ciclo de Carnot.
A figura anterior mostra um exemplo de um ciclo de Carnot ocorrendo no interior de
um cilindro e usando um gás como substância de trabalho.
Este ciclo pode ser representado num diagrama p-v como mostra a figura:
Figura 10.15 Ciclo de Carnot de um gás perfeito no plano pv.
O rendimento do ciclo de Carnot é expresso em termos da razão entre o trabalho gerado
(W) e a energia gasta para produzi-lo (E): η = W E
Da primeira lei e sendo um ciclo ∆h = 0 , porque a substância volta ao seu estado inicial
e supondo que as energias cinéticas e potencial também retornem ao seu valor inicial, temos:
w = ∆Q ⇒ w = Q H − Q L
sendo
Q L = calor cedido a fonte fria
Q H = calor absorvido pela fonte quente
Por outro lado E = Q H
Assim :
W Q − QL
Q
W QH - QL
Q
η= = H
= 1− L η =
=
= 1− L
E
QH
QH
E
QH
QH
Observação:
- Revertendo-se o processo poderíamos definir o coeficiente de eficácia do refrigerador :
1
energia pretendida
QL
β=
=
=
Q
trabalho consumido Q H − Q L
H
−1
QL
Teoremas :
1) É impossível construir um máquina térmica que opere entre dois reservatórios
térmicos e tenha maior rendimento que uma máquina reversível, operando entre os mesmos
reservatórios. ( ηmax = ηCarnot )
2) Todas as máquinas térmicas que operam segundo um ciclo de Carnot, entre 2
reservatórios de temperatura constante, tem o mesmo rendimento.
3) Todo ciclo irreversível que funcione entre as mesmas fontes de temperatura, tem
rendimento menor que o ciclo de Carnot ( ηirrev ⟨ ηCarnot ) .
Observação: independente de qualquer substância particular, temos que:
Q H f (TH )
=
QL
f (TL )
Existem inúmeras relações funcionais que satisfazem esta relação.
Q
T
Lord Kelvin propôs para a escala termodinâmica de temperatura a relação: H = H
Q L TL
(temperatura absoluta)
T
Assim : η = 1 − H
TL
10.3.11.4. Desigualdade de Clausius
δQ
Definição : ∫
≤ 0 ( para todo os ciclos)
T
É um corolário ou uma conseqüência da segunda lei.
É válida tanto para máquina térmica como, para processo reversível ou irreversível.
Observação: a igualdade vale para ciclo reversível e a desigualdade vale para ciclo
irreversível
10.3.11.5. Entropia
h está para a primeira lei assim como s está para a segunda lei no sentido de que é uma
propriedade que possibilita tratar quantitativamente os processos.
Para um ciclo reversível temos:
δQ
∫T
=0
Figura 10.16 Variação da entropia durante um processo irreversível.
Observação: ciclos reversíveis : AB e AC
∫
δQ
T
2A
1A
2A
⇒
∫
1A
δQ
T
1B
⇒
∴∫
∫
= 0⇒
∫
2B
δQ
1B
δQ
T
1C
+
∫
δQ
T
T
1C
=
δQ
2B
2C
δQ
∫
+
∫
2C
T
=0
=0
δQ
T
é a mesma para todas as trajetórias entre 1 e 2 ⇒ só depende dos extremos ⇒ é
T
uma propriedade
2
 δQ 
 δQ 
ds ≡   ⇒ s2 − s1 = ∫  
 T  rev
 T
1
rev
Para processo irreversível, temos :
2
 δQ 
 δQ 
ds ≥  
⇒ s2 − s1 ≥ ∫  
 T  irrev
 T
1
irrev
Algumas relações termodinâmicas envolvendo mudança de entropia são:
T.ds=du+p.dV
T.ds=dh-V.dp
A Figura 10.17 ilustra o princípio do aumento de entropia demonstrado a seguir
Figura 10.17 Variação de entropia para o sistema e vizinhança.
dssist ≥
δQ
T
dsviz = −
dssist + dsviz
(recebe)
δQ
(cede)
To
To>T
1 1
≥ δdsQ −  ⇒ dssist + dsviz ≥ 0
 T To 
dssist isolado ≥ 0
A variação de s para um gás perfeito pode ser calculada por expressões alternativas
deduzidas a abaixo. Tem-se que
dv = c v o ⋅ dt
p R
=
T v
Aplicando as relações termodinâmicas, temos:
2
s2 − s1 = ∫ c v o ⋅
1
dh = c po ⋅ dt
v R
=
T p
v 
dT
+ R ⋅ ln 2 
T
 v1 
P 
T 
s2 − s1 = c v o ⋅ ln 2  − R ⋅ ln 2 
 T1 
 P1 
Qualquer processo ou ciclo pode ser representado num diagrama T-s sendo que a área
abaixo da curva corresponde ao calor.
10.3.11.6. Terceira lei da termodinâmica (Einstein - Plank)
"No zero absoluto de temperatura a entropia de uma substância em forma cristalina é
igual a zero."
Esta lei permite achar os valores absolutos da entropia e calcular os potenciais das
reações químicas.
Obs.: não será utilizada para estudo das máquinas térmicas
10.3.12. Tabelas e Diagramas
Existem várias referências bibliográficas que trazem tabelas e diagramas das
propriedades termodinâmicas para várias substâncias.