GabProb5-Circuitos RC-FIS1051-2008-1

FIS1053 – Projeto de Apoio Eletromagnetismo – 09-Setembro-2011.
Lista de Problemas 6: CIRCUITO RC.
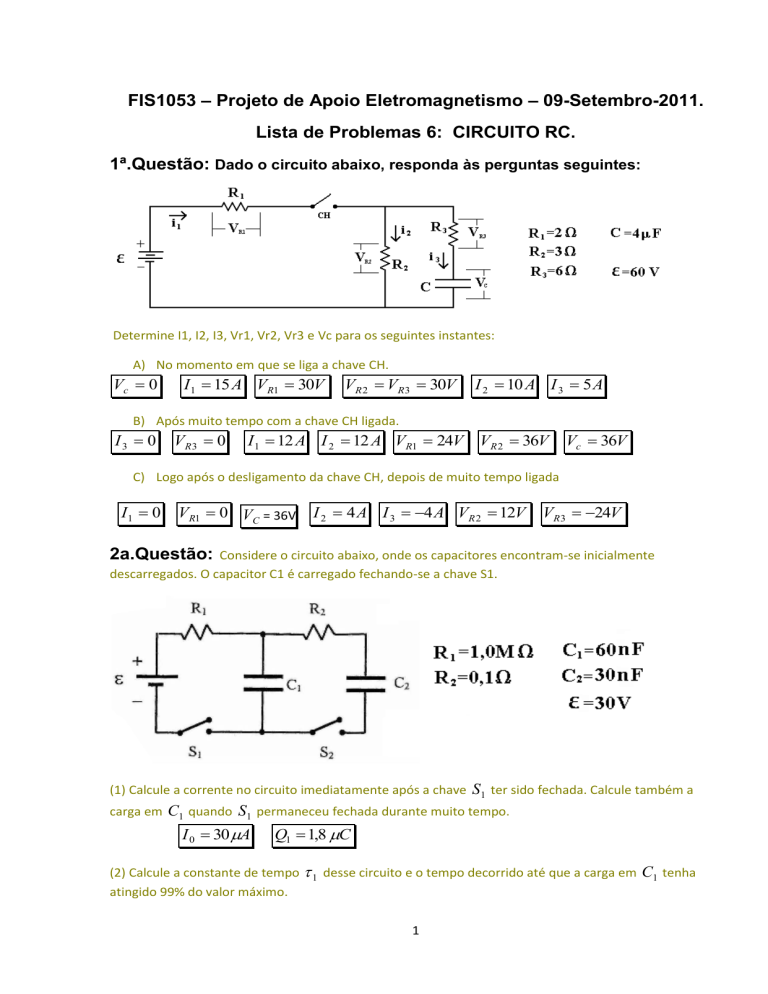
1ª.Questão: Dado o circuito abaixo, responda às perguntas seguintes:
Determine I1, I2, I3, Vr1, Vr2, Vr3 e Vc para os seguintes instantes:
A) No momento em que se liga a chave CH.
Vc  0
I 1  15 A VR1  30V
VR 2  VR3  30V
I 2  10 A I 3  5 A
B) Após muito tempo com a chave CH ligada.
I3  0
VR 3  0
I1  12 A I 2  12 A VR1  24V VR 2  36V
Vc  36V
C) Logo após o desligamento da chave CH, depois de muito tempo ligada
I1  0
VR1  0 VC = 36V
I 2  4 A I 3  4 A VR 2  12V
VR3  24V
2a.Questão:
Considere o circuito abaixo, onde os capacitores encontram-se inicialmente
descarregados. O capacitor C1 é carregado fechando-se a chave S1.
(1) Calcule a corrente no circuito imediatamente após a chave S1 ter sido fechada. Calcule também a
carga em C1 quando S1 permaneceu fechada durante muito tempo.
I 0  30 A
Q1  1,8 C
(2) Calcule a constante de tempo  1 desse circuito e o tempo decorrido até que a carga em C1 tenha
atingido 99% do valor máximo.
1
 1  60 ms
t  276 ms
(3) Agora considere S1 seja aberta, depois de ter permanecido fechada durante muito tempo. O
capacitor C1 é então conectado ao capacitor descarregado C 2 fechando-se a chave S 2 .
(a) Calcule a constante de tempo  2 desse novo circuito.
 2  2 x109 s
(b) Calcule a carga final de cada capacitor e a diferença de potencial final entre suas
placas.
V f  20V
QC 2 f  0,6C
QC1 f  1,2C
(c) Calcule a energia total armazenada em C1 e C 2 no final do processo. Compare
com a energia armazenada em C1 antes de fechar S 2 . Por que elas são diferentes?
U i  27 J
U f  18 J
Parte da carga inicial armazenada no capacitor 1é dissipada pelo resistor , assim
a energia do segundo circuito é menor que a do primeiro.
3ª.Questão:
A figura abaixo mostra um circuito que possui uma bateria que produz uma tensão elétrica
(com
resistência interna nula), uma chave Ch, um resistor R e um capacitor C.
Considerando que o capacitor encontra-se totalmente descarregado antes do fechamento da chave
em t=0, determine:

C  4F
R  2 106 

a) O gráfico de Vc(t)
2
E  10Volts
(b) O gráfico da carga “q” quando
t 
(c) Calcule a energia total fornecida pela fonte:
fonte
Ef = 4x10-7 J.
(d) A energia no capacitor quando este está totalmente carregado.
Uc  2  10 7 joules
(e) Qual foi o destino do restante da energia?
Resp: O restante da energia foi dissipado em forma de calor pelo resistor R.
(f) Quanto tempo é necessário para considerar o capacitor quase totalmente carregado?
com  t  5RC
 q(5RC )  q max 99,3%
FIM
3