MECÂNICA – TURMA UNP – PARTE 1 1. O número Mach é

MECÂNICA – TURMA UNP – PARTE 1
1. O número Mach é definido como a relação entre a velocidade do objeto em movimento e a
velocidade do som no meio. A velocidade transônica está entre a velocidade sub e supersônica.
O período transônico inicia quando começa a aparecer uma barreira de ar em volta das asas do
avião. Quando finalmente o avião ultrapassa a velocidade sônica, segue-se um forte estrondo
sonoro. Nesse momento, o avião excede 1 Mach.
A maior diferença de pressão passa para a frente da aeronave. Esta abrupta diferença de
pressão é a chamada onda de choque, que se estende da traseira à dianteira com uma forma
de cone. Esta onda de choque causa o “boom sônico” que se ouve logo após a passagem do
avião. Quanto maior a velocidade, mais limitado é o denominado cone de Mach.
Podemos dizer que o texto acima refere-se ao avião com uma velocidade acima de:
a) 360 km/h, velocidade aproximada máxima de um carro de Fórmula 1.
b) 1000 km/h, velocidade aproximada máxima do ar.
c) 1200 km/h, velocidade aproximada máxima do som no ar.
d) 2400 km/h, velocidade aproximada máxima do som no vácuo.
e) 3400 km/h, velocidade aproximada máxima do som na água.
2. A gôndola é um meio de transporte comumente usado nos famosos canais de Veneza e
representa um dos principais atrativos turísticos da cidade. Um pedestre caminha no sentido
oeste-leste com velocidade constante de 3 km/h em relação à margem do canal e observa duas
gôndolas em movimento: a primeira, no sentido oeste-leste, com velocidade constante de 10
km/h em relação à margem do canal; e a segunda, no sentido leste-oeste, com velocidade
constante de 6 km/h também em relação à margem do canal. Além disso, um veneziano observa,
de sua janela, o pedestre caminhando no sentido oeste-leste e em sua direção.
Ao colocar o sistema referencial inercial no pedestre, as velocidades relativas da primeira
gôndola, da segunda e do veneziano, em relação ao pedestre, são, respectivamente, de:
a) 7 km/h para o leste, 9 km/h para o oeste, 3 km/h para o oeste.
b) 7 km/h para o oeste, 9 km/h para o leste, 3 km/h para o leste.
c) 13 km/h para o leste, 3 km/h para o oeste, 3 km/h para o leste.
d) 13 km/h para o oeste, 3 km/h para o leste, 3 km/h para o oeste.
e) 13 km/h para o leste, 9 km/h para o oeste, 3 km/h para o leste.
3. Sete crianças saíram em uma van para visitar as obras de um dos estádios da copa do mundo
de 2014, distante 20 km de suas casas. Durante a primeira metade do caminho, a van conseguiu
desenvolver velocidade máxima da pista e chegar a 90 km/h. Porém, para a infelicidade do grupo,
na segunda parte do trajeto, havia muito congestionamento em que levaram 30 minutos.
Portanto, podemos concluir que a velocidade média, em km/h, em todo percurso foi de,
aproximadamente:
a) 32.
b) 38.
c) 42.
d) 48.
e) 62.
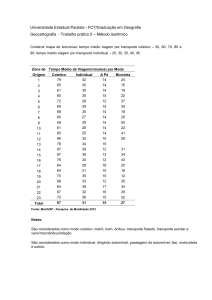
4. O deslocamento Δx de uma partícula em função do tempo t é ilustrado no gráfico a seguir:
Com relação ao movimento mostrado no gráfico, assinale a alternativa CORRETA.
a) A partícula inicia seu movimento com velocidade constante; na sequência, o movimento é
acelerado e, finalmente, a partícula se move com outra velocidade também constante.
b) A velocidade da partícula é constante.
c) A aceleração da partícula é constante.
d) Esse gráfico ilustra o movimento de queda livre de um objeto nas proximidades da superfície
terrestre, onde a resistência do ar foi desprezada.
e) A partícula inicia seu movimento com uma velocidade não nula, mas o movimento é retardado,
e ela finalmente atinge o repouso.
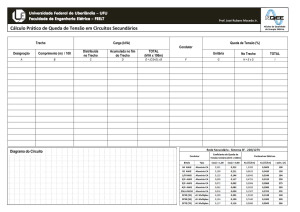
5. Analise a figura a seguir.
Os habitantes de metrópoles convivem com o problema dos congestionamentos de automóveis,
que geram estresse, acidentes, poluição sonora, entre outras consequências. Uma solução para
o problema de mobilidade urbana é o transporte coletivo por linhas de metrô. A figura mostra a
região central da cidade de Brasília. Considere que um indivíduo se desloca diariamente de carro
da posição A, onde mora, até a posição B, onde trabalha, em um percurso de 12 km representado
pela linha tracejada. No horário de rush, a velocidade média dos automóveis é de 12 km/h e, fora
desse horário, é de 42 km/h. Se houvesse em Brasília uma linha de metrô de A até B, como
representado pela linha ponto-tracejada, ela teria 20 km.
Supondo que a velocidade média do metrô seja de 60 km/h, considere as afirmativas a seguir.
I. No horário de rush, o tempo de deslocamento de carro de A até B é maior do que o tempo de
deslocamento por metrô em 1 hora.
II. No horário de rush, o tempo de deslocamento de A até B por metrô é 1/3 do tempo de
deslocamento por carro.
III. Fora do horário de rush, é mais rápido fazer o percurso de A para B de carro.
IV. Fora do horário de rush, considerando que o sistema de metrô tenha melhorado e que sua
velocidade média passe a ser de 70 km/h, então o tempo de deslocamento de A até B tanto por
carro quanto por metrô é igual.
Assinale a alternativa correta.
a) Somente as afirmativas I e II são corretas.
b) Somente as afirmativas I e IV são corretas.
c) Somente as afirmativas III e IV são corretas.
d) Somente as afirmativas I, II e III são corretas.
e) Somente as afirmativas II, III e IV são corretas.
6.
Algumas cidades têm implantado corredores exclusivos para ônibus a fim de diminuir o tempo
das viagens urbanas.
Suponha que, antes da existência dos corredores, um ônibus demorasse 2 horas e 30 minutos
para percorrer todo o trajeto de sua linha, desenvolvendo uma velocidade média de 6 km/h.
Se os corredores conseguirem garantir que a velocidade média dessa viagem aumente para 20
km/h, o tempo para que um ônibus percorra todo o trajeto dessa mesma linha será:
a) 30 minutos.
b) 45 minutos.
c) 1 hora.
d) 1 hora e 15 minutos.
e) 1 hora e 30 minutos.
7. Filas de trânsito são comuns nas grandes cidades, e duas de suas consequências são: o
aumento no tempo da viagem e a irritação dos motoristas. Imagine que você está em uma pista
dupla e enfrenta uma fila. Pensa em mudar para a fila da pista ao lado, pois percebe que, em
determinado trecho, a velocidade da fila ao lado é 3 carros/min. enquanto que a velocidade da
sua fila é 2 carros /min.
Considere o comprimento de cada automóvel igual a 3 m.
Assinale a alternativa correta que mostra o tempo, em min, necessário para que um automóvel
da fila ao lado que está a 15m atrás do seu possa alcançá-lo.
a) 2
b) 3
c) 5
d) 4
8. O desrespeito às leis de trânsito, principalmente àquelas relacionadas à velocidade permitida
nas vias públicas, levou os órgãos regulamentares a utilizarem meios eletrônicos de fiscalização:
os radares capazes de aferir a velocidade de um veículo e capturar sua imagem, comprovando
a infração ao Código de Trânsito Brasileiro.
Suponha que um motorista trafegue com seu carro à velocidade constante de 30 m/s em uma
avenida cuja velocidade regulamentar seja de 60 km/h. A uma distância de 50 m, o motorista
percebe a existência de um radar fotográfico e, bruscamente, inicia a frenagem com uma
desaceleração de 5 m/s2.
Sobre a ação do condutor, é correto afirmar que o veículo:
a) não terá sua imagem capturada, pois passa pelo radar com velocidade de 50 km/h.
b) não terá sua imagem capturada, pois passa pelo radar com velocidade de 60 km/h.
c) terá sua imagem capturada, pois passa pelo radar com velocidade de 64 km/h.
d) terá sua imagem capturada, pois passa pelo radar com velocidade de 66 km/h.
e) terá sua imagem capturada, pois passa pelo radar com velocidade de 72 km/h.
9. Um objeto tem a sua posição (x) em função do tempo (t) descrito pela parábola conforme o
gráfico.
Analisando-se esse movimento, o módulo de sua velocidade inicial, em m/s, e de sua aceleração,
em m/s2, são respectivamente iguais a:
a) 10 e 20.
b) 10 e 30.
c) 20 e 10.
d) 20 e 30.
e) 30 e 10.
10. Toda manhã, um ciclista com sua bicicleta pedala na orla de Boa Viagem durante 2 horas.
Curioso para saber sua velocidade média, ele esboçou o gráfico velocidade escalar em função
do tempo, conforme a figura abaixo. A velocidade média, em km/h, entre o intervalo de tempo de
0 a 2 h, vale:
a) 3
b) 4
c) 6
d) 8
e) 9
11.
Com a intenção de se preparar para uma maratona, Branca de neve e Encantado
começaram um treino diário de corrida e pediram ajuda para a experiente maratonista Fada
madrinha. A instrutora, então, com a ajuda de um dispositivo eletrônico de última geração
conhecido como radar, plotou gráficos da velocidade de cada um pelo tempo em que ficava
observando.
Certo dia, apresentou os gráficos aos dois, utilizando para isso a mesma escala nos eixos, sendo
VE a velocidade de Encantado e VB a velocidade de Branca de neve.
Baseando-se nos gráficos apresentados, durante o intervalo de tempo T observado, podemos
concluir corretamente que:
a) a aceleração impressa no início por Encantado foi maior do que a de Branca de neve.
b) a velocidade máxima atingida por Branca de neve foi maior do que a de Encantado.
c) Encantado foi mais longe que Branca de neve.
d) Branca de neve percorreu uma distância maior do que Encantado.
e) a velocidade média de Branca de neve é menor do que a de Encantado.
12. Um motorista dirigia por uma estrada plana e retilínea quando, por causa de obras, foi
obrigado a desacelerar seu veículo, reduzindo sua velocidade de 90 km/h (25 m/s) para 54 km/h
(15 m/s). Depois de passado o trecho em obras, retornou à velocidade inicial de 90 km/h. O
gráfico representa como variou a velocidade escalar do veículo em função do tempo, enquanto
ele passou por esse trecho da rodovia.
Caso não tivesse reduzido a velocidade devido às obras, mas mantido sua velocidade constante
de 90 km/h durante os 80 s representados no gráfico, a distância adicional que teria percorrido
nessa estrada seria, em metros, de:
a) 1 650.
b) 800.
c) 950.
d) 1 250.
e) 350.
TEXTO PARA A PRÓXIMA QUESTÃO:
Andar de bondinho no complexo do Pão de Açúcar no Rio de Janeiro é um dos passeios aéreos
urbanos mais famosos do mundo. Marca registrada da cidade, o Morro do Pão de Açúcar é
constituído de um único bloco de granito, despido de vegetação em sua quase totalidade e tem
mais de 600 milhões de anos.
13. O passeio completo no complexo do Pão de Açúcar inclui um trecho de bondinho de
aproximadamente 540 m, da Praia Vermelha ao Morro da Urca, uma caminhada até a segunda
estação no Morro da Urca, e um segundo trecho de bondinho de cerca de 720 m, do Morro da
Urca ao Pão de Açúcar. A velocidade escalar média do bondinho no primeiro trecho é
v1  10,8 km / h e, no segundo, é v2  14,4 km / h. Supondo que, em certo dia, o tempo gasto
na caminhada no Morro da Urca somado ao tempo de espera nas estações é de 30 minutos, o
tempo total do passeio completo da Praia Vermelha até o Pão de Açúcar será igual a:
a) 33 min.
b) 36 min.
c) 42 min.
d) 50 min.
14. Um avião decola de um aeroporto e voa 100 km durante 18 min no sentido leste; a seguir,
seu piloto aponta para o norte e voa mais 400 km durante 1 h; por fim, aponta para o oeste e voa
os últimos 50 km, sempre em linha reta, em 12 min, até pousar no aeroporto de destino. O módulo
de sua velocidade vetorial média nesse percurso todo terá sido, em km∕h, de aproximadamente:
a) 200.
b) 230.
c) 270.
d) 300.
e) 400.
15. O gráfico da figura mostra a posição em função do tempo de uma pessoa que passeia em
um parque.
Calcule a velocidade média em m/s desta pessoa durante todo o passeio, expressando o
resultado com o número de algarismos significativos apropriados.
a) 0,50
b) 1,25
c) 1,50
d) 1,70
e) 4,00
16. Um motorista viaja da cidade A para a cidade B em um automóvel a 40 km/h. Certo
momento, ele visualiza no espelho retrovisor um caminhão se aproximando, com velocidade
relativa ao carro dele de 10 km/h, sendo a velocidade do caminhão em relação a um referencial
inercial parado é de 50 km/h. Nesse mesmo instante há uma bobina de aço rolando na estrada
e o motorista percebe estar se aproximando da peça com a mesma velocidade que o caminhão
situado à sua traseira se aproxima de seu carro. Com base nessas informações, responda: a
velocidade a um referencial inercial parado e a direção da bobina de aço é:
a) 10 km/h com sentido de A para B
b) 90 km/h com sentido de B para A
c) 40 km/h com sentido de A para B
d) 50 km/h com sentido de B para A
e) 30 km/h com sentido de A para B
17. Um automóvel percorre uma estrada reta de um ponto A para um ponto B. Um radar detecta
que o automóvel passou pelo ponto A a 72 km/h. Se esta velocidade fosse mantida constante, o
automóvel chegaria ao ponto B em 10 min. Entretanto, devido a uma eventualidade ocorrida na
metade do caminho entre A e B, o motorista foi obrigado a reduzir uniformemente a velocidade
até 36 km/h, levando para isso, 20 s. Restando 1 min. para alcançar o tempo total inicialmente
previsto para o percurso, o veículo é acelerado uniformemente até 108 km/h, levando para isso,
22 s, permanecendo nesta velocidade até chegar ao ponto B. O tempo de atraso, em segundos,
em relação à previsão inicial, é:
a) 46,3
b) 60,0
c) 63,0
d) 64,0
e) 66,7
18. Seja o gráfico da velocidade em função do tempo de um corpo em movimento retilíneo
uniformemente variado representado abaixo.
Considerando a posição inicial desse movimento igual a 46 m, então a posição do corpo no
instante t = 8 s é:
a) 54 m.
b) 62 m.
c) 66 m.
d) 74 m.
19. Duas partículas, a e b, que se movimentam ao longo de um mesmo trecho retilíneo tem as
suas posições (S) dadas em função do tempo (t), conforme o gráfico abaixo.
O arco de parábola que representa o movimento da partícula b e o segmento de reta que
representa o movimento de a tangenciam-se em t  3 s. Sendo a velocidade inicial da partícula
b de 8 m s, o espaço percorrido pela partícula a do instante t  0 até o instante t  4 s, em
metros, vale:
a) 3,0
b) 4,0
c) 6,0
d) 8,0
20. O jipe-robô Curiosity da NASA chegou a Marte, em agosto de 2012, carregando consigo
câmeras de alta resolução e um sofisticado laboratório de análises químicas para uma rotina de
testes. Da Terra, uma equipe de técnicos comandava seus movimentos e lhe enviava as tarefas
que deveria realizar.
Imagine que, ao verem a imagem de uma rocha muito peculiar, os técnicos da NASA, no desejo
de que o Curiosity a analisasse, determinam uma trajetória reta que une o ponto de observação
até a rocha e instruem o robô para iniciar seu deslocamento, que teve duração de uma hora.
Nesse intervalo de tempo, o Curiosity desenvolveu as velocidades indicadas no gráfico.
O deslocamento total realizado pelo Curiosity do ponto de observação ao seu destino foi, em
metros:
a) 9.
b) 6.
c) 4.
d) 2.
e) 1.
21. Um carro deslocou-se por uma trajetória retilínea e o gráfico qualitativo de sua velocidade
(v), em função do tempo (t), está representado na figura.
Analisando o gráfico, conclui-se corretamente que
a) o carro deslocou-se em movimento uniforme nos trechos I e III, permanecendo em repouso
no trecho II.
b) o carro deslocou-se em movimento uniformemente variado nos trechos I e III, e em movimento
uniforme no trecho II.
c) o deslocamento do carro ocorreu com aceleração variável nos trechos I e III, permanecendo
constante no trecho II.
d) a aceleração do carro aumentou no trecho I, permaneceu constante no trecho II e diminuiu no
trecho III.
e) o movimento do carro foi progressivo e acelerado no trecho I, progressivo e uniforme no trecho
II, mas foi retrógrado e retardado no trecho III.
22. Um automóvel desloca-se por uma estrada retilínea plana e horizontal, com velocidade
constante de módulo v. Em certo momento, o automóvel alcança um longo caminhão. A
oportunidade de ultrapassagem surge e o automóvel é acelerado uniformemente até que fique
completamente à frente do caminhão. Nesse instante, o motorista "alivia o pé" e o automóvel
reduz a velocidade uniformemente até voltar à velocidade inicial v. A figura abaixo apresenta
cinco gráficos de distância (d)  tempo (t). Em cada um deles, está assinalado o intervalo de
tempo  Δt  em que houve variação de velocidade.
Escolha qual dos gráficos melhor reproduz a situação descrita acima.
a)
b)
c)
d)
e)
23. Para melhorar a mobilidade urbana na rede metroviária é necessário minimizar o tempo
entre estações. Para isso a administração do metrô de uma grande cidade adotou o seguinte
procedimento entre duas estações: a locomotiva parte do repouso em aceleração constante por
um terço do tempo de percurso, mantém a velocidade constante por outro terço e reduz sua
velocidade com desaceleração constante no trecho final, até parar.
Qual é o gráfico de posição (eixo vertical) em função do tempo (eixo horizontal) que representa
o movimento desse trem?
a)
b)
c)
d)
e)
24. O gráfico abaixo indica a posição (S) em função do tempo (t) para um automóvel em
movimento num trecho horizontal e retilíneo de uma rodovia.
Da análise do gráfico, pode-se afirmar que o automóvel:
a) está em repouso, no instante 1 min.
b) possui velocidade escalar nula, entre os instantes 3 min e 8 min.
c) sofreu deslocamento de 4 km, entre os instantes 0 min e 3 min.
d) descreve movimento progressivo, entre os instantes 1 min e 10 min.
e) tem a sua posição inicial coincidente com a origem da trajetória.
25. Ao abrir uma garrafa de refrigerante com gás, muitas bolhas de gás carbônico ali formadas
sobem desde o fundo da garrafa com um movimento acelerado. Supondo-se que as bolhas têm
o mesmo tamanho e a mesma quantidade de gás durante toda subida e desprezando-se
quaisquer perdas de energia por resistência ao movimento. Dos gráficos a seguir aqueles que
representam, respectivamente, a posição e a velocidade das bolhas são:
a) I e IV
b) I e VI
c) II e V
d) II e VI
e) III e V
26. Quatro corpos 1, 2, 3 e 4 movem-se em uma trajetória retilínea e o diagrama velocidade
versus tempo de cada um deles é mostrado a seguir. Considerando que todos os corpos partiram
do mesmo ponto, é CORRETO afirmar que o corpo que está mais próximo do ponto de partida
no instante t = 10s é o representado na alternativa:
a) corpo 1
b) corpo 4
c) corpo 2
d) corpo 3
27. Um móvel se desloca numa trajetória retilínea e seus diagramas de velocidade e espaço
em relação ao tempo são mostrados a seguir:
O móvel muda o sentido de seu movimento na posição:
a) 10 m
b) 30 m
c) 5 m
d) 20 m
28. Rua da Passagem
Os automóveis atrapalham o trânsito.
Gentileza é fundamental.
Não adianta esquentar a cabeça.
Menos peso do pé no pedal.
O trecho da música, de Lenine e Arnaldo Antunes (1999), ilustra a preocupação com o trânsito
nas cidades, motivo de uma campanha publicitária de uma seguradora brasileira. Considere dois
automóveis, A e B, respectivamente conduzidos por um motorista imprudente e por um motorista
consciente e adepto da campanha citada. Ambos se encontram lado a lado no instante inicial t =
0 s, quando avistam um semáforo amarelo (que indica atenção, parada obrigatória ao se tornar
vermelho). O movimento de A e B pode ser analisado por meio do gráfico, que representa a
velocidade de cada automóvel em função do tempo.
As velocidades dos veículos variam com o tempo em dois intervalos: (I) entre os instantes 10s e
20s; (II) entre os instantes 30s e 40s. De acordo com o gráfico, quais são os módulos das taxas
de variação da velocidade do veículo conduzido pelo motorista imprudente, em m/s 2, nos
intervalos (I) e (II), respectivamente?
a) 1,0 e 3,0
b) 2,0 e 1,0
c) 2,0 e 1,5
d) 2,0 e 3,0
e) 10,0 e 30,0
Gabarito:
Resposta
[C]
da
questão
1:
A velocidade de propagação do som no ar é cerca de 340 m/s. Passando para km/h:
v  340
m 0,34 km

 0,34  3.600 km/h 
1
s
h
3.600
Resposta
[A]
v  1.224 km/h
da
questão
2:
Adotando o sentido positivo para o leste, em relação ao solo, temos:
- velocidade do pedestre: vP = 3 km/h;
- velocidade da gôndola 1: vG1 = 10 km/h;
- velocidade da gôndola 2: vG2 = - 6 km/h;
- velocidade do veneziano 1: vV = 0 km/h.
Se dois móveis, A e B, se deslocam na mesma direção, a velocidade de A em relação a B (vA/B)
é dada por:
v A/B  v A  vB.
Aplicando essa expressão às situações propostas:
v G1/P  v G1  vP  10  3  7 km / h (para o leste)

v G2/P  vG2  vP  6  3  9 km / h (para o oeste)
v
 V/P  v V  vP  0  3  3 km / h (para o oeste)
Resposta
[A]
da
questão
3:
Dados: ΔS1  10km; v1  90km / h; ΔS2  10km; Δt2  30min.
Calculemos o tempo do primeiro trecho e o tempo total:

ΔS1 10 1
Δt1  v  90  9 h
1 1 29
11

1
 Δt   
 Δt 
h.

9 2
18
18
Δt  30min  1 h
 2
2
Calculando a velocidade média:
vm 
ΔS1  ΔS2
20
360


11
Δt
11
18
Resposta
[E]

vm  32,72 km/h.
da
questão
4:
No gráfico do espaço em função do tempo, a declividade da curva nos dá a velocidade escalar.
Ou seja, a velocidade escalar é numericamente igual a tangente do ângulo que a curva faz com
o eixo dos tempos.
Assim:
v0  tg α0  0; v1  tg α1 .
Analisando o gráfico, vemos que a declividade vai diminuindo, até que em t  4 s  α4  0,
quando a velocidade se anula. Portanto, o movimento é retardado com velocidade final nula.
Resposta
[E]
da
questão
5:
[I] Incorreta. No horário de rush, o tempo de deslocamento de carro de A até B é igual ao o
tempo de deslocamento por metrô em 1 hora.
ΔScarro 12
Δtcarro 

 Δtcarro  1 h.
vrush
12
[II] Correta.

ΔScarro 12

 Δtcarro  1 h
Δtcarro 
vrush
12


ΔSmetrô 20
1
Δt


 Δtmetrô 
h
 metrô
vmetrô
60
3

 Δtmetrô 
[III] Correta.

ΔScarro 12
2

 Δtcarro 
h  0,29 h
Δtcarro 
vrush
42
7


ΔSmetrô 20
1
Δt


 Δtcarro 
h  0,33 h
 metrô
vmetrô
60
3

[IV] Correta.

ΔScarro 12
2

 Δtcarro 
h
Δtcarro 
vrush
42
7


ΔSmetrô 20
2
Δt


 Δtcarro 
 metrô
vmetrô
70
7

Resposta
[B]
1
Δtcarro .
3
 Δtcarro  Δtmetrô
 Δtcarro  Δtmetrô
da
questão
Dados v1  6km / h; v2  20km / h; Δt1  2h e 30min  150min.
O espaço percorrido é o mesmo nos dois casos.
ΔS1  ΔS2  v1 Δt1  v 2 Δt 2  6  150  20  Δt 2  Δt 2 
Δt 2  45 min.
900

20
6:
Resposta
[C]
da
questão
7:
Interpretemos “alcançar” como sendo a frente do carro de trás chegar à traseira do meu carro.
A velocidade do carro ao lado (v1) e a do meu carro (v2) são:

carros 3  3 m 
m

 v1  9
v 1  3

min
min
min

 v  2 carros  2  3 m   v  6 m
2
 2
min
min
min
Usando velocidade relativa:
ΔSrel
15
15
vrel 
 96 
 Δt 
 Δt  5 s.
Δt
Δt
3
Resposta
[E]
da
questão
8:
Da equação de Torricelli:
v 2  v 02  2 a ΔS  v 2  302  2  5  50  v 2  400  v  20 m/s 
v  72 km/h.
Resposta
[C]
da
questão
9:
Dados do gráfico: x0  0; t  2s  (v  0 e x  20m).
Como o gráfico é um arco de parábola, trata-se de movimento uniformemente variado (MUV).
Usando, então, as respectivas equações:
v  v 0  a t  0  v 0  a  2   v 0  - 2 a I

t2s 
a 2
a 2
 x  v 0 t  t  20  v 0  2    2   20  2 v 0  2 a II

2
2
(I) em (II):
20  2  2a   2 a
 2 a   20

a  10 m/s2.
Em (I):
v 0   2 a  v 0   2  10  
Resposta
[D]
v 0  20 m/s.
da
questão
10:
A “área” no diagrama vt é numericamente igual ao espaço percorrido (d).
Dividimos a figura em 2 partes e calculamos a “área” da seguinte forma:
d  A1  trapézio   A 2 retângulo   10  2   1/2 10  1  6  10  16 km.
Mas o tempo total gasto é t = 2 h.
Então a velocidade média é:
vm  d/t  16/2  8 km/h.
Resposta
[D]
da
questão
11:
Tomando como unidade (u) o lado de cada quadrículo, e usando a propriedade do gráfico da
velocidade  tempo, as áreas dos trapézios fornecem as distâncias percorridas por Encantado
(dE) e Branca de neve (dB):

5 1
dE  2  4  dE  12 u.

d  6  4  3  d  15 u.
B
 B
2
Resposta
[E]

da
dB  dE.
questão
12:
A distância (D) pedida é numericamente igual à área hachurada no gráfico.
D
50  20
 10  D  350 m.
2
Resposta
[B]
da
questão
13:
Dados: D1 = 540 m; v1 = 10,8 km/h = 3 m/s; D2 = 720 m; v2 = 14,4 km/h = 4 m/s; Δtc = 30 min.
Calculando o tempo total:
D1 540

Δt1  v  3  180 s  3min.
1


D2 720

 180 s  3min.
Δt 2 
v2
4

Δt  30min.
 c

 Δt  Δt1  Δt 2  Δt c  3  3  30 
Δt  36min.
Resposta
[C]
da
questão
14:
As figuras abaixo representam os sucessivos deslocamentos vetoriais e seus módulos, bem
como o deslocamento resultante.
Calculando o módulo do deslocamento resultante:
d2  502  4002  d2  162.500  d  403 km.
O tempo total gasto nesses deslocamentos é:
12 
 18
t  
1
  0,3  1  0,5  h  1,5 h.
60 
 60
A velocidade vetorial média tem módulo:
d 403
vm 

 vm  268,7 km / h
t 1,5

vm  270 km / h.
Resposta
[B]
Vm 
da
questão
15:
da
questão
16:
ΔS 50  0

 1,25 m/s.
Δt 40  0
Resposta
[E]
Admitindo que a bobina role para a direita, podemos escrever:
50  40  40  V  V  30km / h.
Resposta
[D]
da
questão
17:
- Inicialmente vamos determinar as previsões iniciais:
V  72km / h  20m / s
Δt  10min  600s
V
ΔS
ΔS
 20 
 ΔS  12000m
Δt
600
O enunciado nos informa que: “devido a uma eventualidade ocorrida na metade do caminho”, ou
seja, o automóvel percorreu ΔS1  6000m em Δt1  300s , restando mais 6000m que devem ser
percorridos também em 300s, para o automóvel chegar em B no tempo previsto.
- O enunciado nos informa que após a metade do caminho, o motorista foi obrigado a reduzir
uniformemente a velocidade, levando 20s para isso e mantendo tal velocidade até restar 1min
para alcançar o tempo total inicialmente previsto.
Analisando a diminuição da velocidade:
V0  20m / s
V  36km / h  10m / s
Δt 2  20s
V  V0  a  Δt  10  20  a  20  a  0,5 m / s2
V 2  V02  2  a  ΔS  102  202  2  ( 0,5)  ΔS  ΔS 2  300m
Analisando o deslocamento com velocidade constante até restar 60s (1min) para alcançar o
tempo total previsto:
tprevisto  600s
“até restar 60s (1min)”: 600  60  540s
tpercorrido  Δt1  Δt 2  300  20  320s
Δt 3  540  320  Δt 3  220s
V  10m / s
ΔS
ΔS
V
 10 
 ΔS3  2200m
Δt
220
- Por último o veículo é acelerado uniformemente até 108 km/h, levando para isso, 22 s,
permanecendo nesta velocidade até chegar ao ponto B.
Analisando o aumento da velocidade:
V0  10m / s
V  108km / h  30m / s
Δt 4  22s
V  V0  a  Δt  30  10  a  22  a  0,91m / s2
V 2  V02  2  a  ΔS  302  102  2  0,91 ΔS  ΔS 4  440m
Analisando o deslocamento com velocidade constante até chegar ao ponto B:
ΔSpercorrido  ΔS1  ΔS2  ΔS3  ΔS4
ΔSpercorrido  6000  300  2200  440  8940m
ΔS5  ΔStotal  ΔSpercorrido  12000  8940  ΔS5  3060m
V  30m / s
V
ΔS
3060
 30 
 Δt5  102s
Δt
Δt
- O tempo de atraso:
Δt total  Δt1  Δt 2  Δt3  Δt 4  Δt5
Δt total  300  20  220  22  102  Δt total  664s
tatraso  Δt total  Δtprevisto  664  600
tatraso  64s
Resposta
[B]
Dado: S0 = 46 m.
da
questão
18:
Do gráfico:

t  0  v0  10 m/s


t  5 s  v  0
 a
Δv 0  10

 a  -5 m/s2.
Δt
50
Aplicando a função horária do espaço para o instante t = 8 s:
a
-2
2
S  S0  v 0 t  t 2  S  46  10  8    8   46  80  64 
2
2
S  62 m.
Resposta
[D]
da
questão
19:
Dados: v0b = 8 m/s.
O gráfico nos mostra que no instante t = 4 s a partícula b inverte o sentido de seu movimento,
ou seja, sua velocidade se anula nesse instante (vb = 0).
vb  v0b  a t  0  8  a  4  a  2 m / s2.
Para o instante t = 3 s:
vb  8  2  3   vb  2 m / s.
Se a reta tangencia a parábola no instante t = 3 s, as velocidades das duas partículas são iguais
nesse instante. Então:
t  3 s  va  vb  2 m / s.
Como o movimento da partícula a é uniforme, o espaço percorrido por ela até t = 4 s é:
Sa  v a t  Sa  2  4   Sa  8,0 m.
Resposta
[B]
da
questão
20:
Para calcular o deslocamento do jipe-robô, usamos a propriedade do gráfico v  t, calculando a
“área” destacada no gráfico abaixo.
ΔS 
20  15
15  10
10  7,5
10  5
55
 15 
 5  10  10  2 
5 
 10 

2
2
2
2
2
ΔS  262,5  62,5  100  87,5  75  12,5  600 cm 
ΔS  6 m.
Resposta
[B]
da
questão
21:
Analisando cada um dos trechos:
[I] o módulo da velocidade escalar cresce linearmente com o tempo: o movimento é
uniformemente variado, acelerado.
[II] o módulo da velocidade escalar é constante e não nulo: o movimento é uniforme.
[III] o módulo da velocidade escalar decresce linearmente com o tempo: o movimento é
uniformemente variado, retardado.
Resposta
[A]
da
questão
22:
[A] Verdadeira. Os gráficos apresentados são de deslocamento por tempo. Como o enunciado
nos informa que o automóvel desenvolve velocidade constante de módulo v, no início e no final,
teremos a função d  v.t de primeiro grau, ou seja, o gráfico deverá ser uma reta no inicio e no
final o que é satisfeito por todas as alternativas.
No intervalo Δt o automóvel aumenta e em seguida diminui sua velocidade, ambos
a.t 2
de segundo grau, ou seja, o gráfico
2
deverá ser duas parábolas seguidas, a primeira com concavidade para cima, o que representa o
aumento da velocidade e a segunda com a concavidade para baixo, o que representa a
diminuição da velocidade, sendo a alternativa [A] a única que satisfaz o enunciado.
uniformemente, o que nos remete à função d  v.t 
[B] Falsa. O gráfico apresenta uma reta no intervalo Δt .
[C] Falsa. O gráfico apresenta uma reta no intervalo Δt .
[D] Falsa. O gráfico apresenta uma reta no intervalo Δt .
[E] Falsa. O gráfico apresenta, aparentemente, duas parábolas, porém com as concavidades
invertidas.
Resposta
[C]
da
questão
23:
1º Trecho: movimento acelerado (a > 0)  o gráfico da posição em função do tempo é uma
curva de concavidade para cima.
2º Trecho: movimento uniforme (a = 0)  o gráfico da posição em função do tempo é um
segmento de reta crescente.
3º Trecho: movimento desacelerado (a < 0)  o gráfico da posição em função do tempo é uma
curva de concavidade para baixo.
Resposta
[B]
da
questão
24:
Note que entre 3 e 8 min a posição não varia. Portanto, o carro está parado.
Resposta
[D]
da
questão
25:
Durante a subida, agem na bolha o empuxo ( E ) e o peso ( P ), uma vez que as forças resistivas
são desprezíveis. Se, conforme supõe o enunciado, as bolhas têm o mesmo tamanho (ou mesmo
volume) e a mesma quantidade de gás, o empuxo e o peso são constantes.
Se uma bolha sobe em movimento acelerado, então E > P.
Aplicando o princípio fundamental da dinâmica:
Fres = E – P = m a.
Se E e P são constantes, a resultante é constante, logo a aceleração também é constante. Isso
significa que o movimento é uniformemente acelerado. Como a bolha parte do repouso, a
velocidade inicial é nula, portanto a função horária da velocidade é:
v = at. O gráfico da velocidade em função do tempo é uma reta, o que nos leva ao gráfico VI.
A função horária do espaço (S) para um movimento uniformemente variado, a partir do repouso,
supondo posição inicial nula é:
1
S  a t 2 . O gráfico correspondente é um arco de parábola que passa pela origem, o que nos
2
remete ao gráfico II.
Resposta
[D]
da
questão
26:
Resposta
[B]
da
questão
27:
Como o gráfico da velocidade em função do tempo é uma reta, trata-se de movimento
uniformemente variado. Desses gráficos podemos tirar que:
S0 = 0; v0 = 10 m/s.
Podemos ainda concluir que no instante t = 2 s a velocidade se anula (v = 0), ou seja, o móvel
inverte o sentido de seu movimento, uma vez que a trajetória é retilínea.
Calculando o espaço percorrido de 0 a 2 s pela “área” no primeiro gráfico:
S =
2  10
 10 m.
2
Mas:
S = S – S0  10 = S – 20  S = 30 m.
Resposta
[D]
da
questão
28:
Pelo gráfico, percebe-se que o motorista imprudente é o condutor do veículo A, que recebe
acelerações e desacelerações mais bruscas.
30  10 20
 |a(I)| = 2,0 m/s2.

20  10 10
0  30
30

De 30 s a 40 s: a(II) =
 a(II) = 3,0 m/s2.
40  30
10
De 10 s a 20 s: |a(I)| =