Apêndice B – conhecimentos prévios Revendo conceitos de

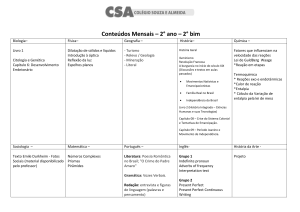
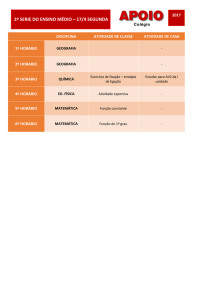
Portfolio de:
Apêndice B – conhecimentos prévios
Revendo conceitos de fenômenos de transporte e termodinâmica...
conceitos básicos – definições:
volume de controle (VC):
energia (U):
“é uma região finita, cuidadosamente escolhida por um analista, com
contornos abertos pelos quais se permite que massa, quantidade de
movimento e energia cruzem”. (White, Mecânica dos fluidos, p. 23)
“capacidade que um corpo, uma substância, um sistema físico tem de realizar
trabalho”. ((na língua portuguesa os primeiros registros da palavra energia datam de 1563) – dicionário Houaiss,
esta idéia remonta a Aristóteles)
energia interna:
“é a fração de energia total de um sistema físico que é determinada apenas
por seu estado de repouso e correspondente à soma das energias cinéticas e
potenciais dos componentes deste sistema, seu valor absoluto não pode ser
determinado, porém é possível medir sua variação que para um sistema
fechado, corresponde ao calor absorvido pelo sistema”. (dicionário Houaiss)
“A variação de energia interna consiste em um componente
sensível ou térmico, que leva em consideração os movimentos
de translação, rotação ou vibração dos átomos/ moléculas que
compõem a matéria; um componente latente que está
relacionado às forças intermoleculares que influenciam as
mudanças de fase entre os estados sólido, líquido e gasoso; um
componente químico que compreende a energia armazenada
nas ligações químicas entre os átomos; e um componente
nuclear que representa as forças de coesão existente nos núcleos
dos átomos.” (Incropera & De Witt, p. 8)
“se refere à energia das moléculas que constituem a substância
de um corpo. Acredita-se que as moléculas de qualquer
substância estão em incessante movimento e possuem energia
cinética de translação, de rotação e de vibração. Além da energia
cinética, as moléculas de qualquer substância possuem energia
potencial em virtude das interações dos respectivos campos de
força. Numa escala submolecular, há energia associada aos
elétrons e aos núcleos atômicos e energia de ligação resultante
das forças que mantém os átomos reunidos em moléculas” (Smith,
J.M.; Van Ness, H.C. Introdução à Termodinâmica da Engenharia Química.).
temperatura (T):
“grau ou quantidade de calor existente num corpo”.
(primeiros registros na língua
portuguesa – 1813 - dicionário Houaiss da língua portuguesa)
"Temperatura é uma medida do nível de energia interna". (White, p. 10)
"The degree of heat of A, or of any body in thermal equilibrium with A, can
thus be very simply defined by the volume of A, or, as is usual, by the
difference between the volume of A and an arbitrarily selected normal
volume, namely, the volume of A when in thermal equilibrium with melting
ice under atmospheric pressure. This volumetric difference, which, by an
appropriate choice of unit, is made to read 100 when A is in contact with
steam under atmospheric pressure is called the temperature in degrees
Centigrade with regard to A as thermometric substance. Two bodies of equal
(Max Planck
temperature are, therefore, in thermal equilibrium, and vice versa”.
– Treatise on thermodynamics – tradução de 1926 de sua obra de 1922)
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
7
Portfolio de:
“é um parâmetro que expressa a energia cinética média das
moléculas“(Mahan)
“é o conteúdo médio de calor por átomo de certa quantidade de
matéria, e somente matéria pode ter temperatura”. (Asimov).
energia térmica:
entalpia (H):
entropia:
“qualquer troca de energia acompanhada da mudança de
temperatura”. (dicionário Houaiss)
“conteúdo de calor de um sistema cuja expressão em outro termodinâmico é
definida pela soma de sua energia interna com o produto do volume do
sistema pela pressão a que está submetido” (primeiro registro na língua portuguesa é de 1924,
dicionário Houaiss)
, ou seja, é uma quantidade termodinâmica derivada da energia
interna definida como sendo: H = U + PV (P ... pressão e V ... volume)
“o termo entropia foi introduzido em 1840 pelo físico alemão Rudolf
Clausius, para caracterizar o grau de uniformidade com que a energia, sob
qualquer forma, está distribuída. Quanto mais uniformemente distribuída
estiver, maior a entropia. Quando a energia estiver distribuída de maneira
completamente uniforme, a entropia atinge o valor máximo para o sistema
em questão. (...) (exemplo: pondo-se um objeto quente em contato com
outro frio, o calor flui de tal maneira que o objeto quente se esfria e o objeto
frio fica mais quente, até que ambos atinjam a mesma temperatura)” (Asimov)
primeira lei da termodinâmica: “é uma exposição geral sobre o comportamento da função de estado
energia e diz: a energia do universo é constante. Esta lei, assim como a
segunda lei da termodinâmica, não são deduzidas. Surgiram de nossas
observações sobre o comportamento da matéria como um todo e resumem as
características universais de toda nossa experiência. Sua generalidade foi
repetidamente demonstrada e esperamos que conclusões nelas baseadas
sejam válidas em quaisquer nova experiência que fizermos” (Mahan).
segunda lei da termodinâmica: “é uma exposição geral sobre o comportamento da função de estado
entropia”. “Entropia é uma função de estado. Em um processo reversível, a
entropia do universo é constante. Em um processo irreversível, a entropia do
universo aumenta. Para provar a segunda lei iremos demonstrar que negá-la
implica em que os gases possam comprimir-se espontaneamente e que o
calor pode fluir espontaneamente de regiões frias a regiões quentes”(Mahan).
“Clausius afirmou que havia uma regra geral na natureza, segundo a qual as
diferenças de concentração de energia tendem a nivelar-se. Em outras
palavras, a entropia aumenta com o decorrer do tempo. A sugestão de
Clausius de que a entropia aumenta com o tempo parecia enunciar algo
fundamental e por isso é chamada de segunda lei da termodinâmica”. ”Podese mostrar que todo processo que nível a concentração de energia é
acompanhado de um aumento da desordem. Por conseguinte, essa tendência
no aumento da desordem no universo através dos movimentos ao acaso das
partículas que o constituem é apenas outro aspecto da segunda lei. Assim
sendo, a entropia pode ser considerada uma medida da desordem presente no
universo”. (Asimov)
Propriedades específicas:
propriedade dividida pela massa ou número de moles ou pelo volume(menos
comum)
; e.g. energia interna específica:
H=
H
H
ou H! =
m
n
 ∂H 
Capacidade Calorífica: a pressão constante: c p = 
 em (J/kg.K) ou (J/mol.K)
 ∂T  P
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
8
Portfolio de:
 ∂U 
a volume constante: cv = 
 em (J/kgK) ou (J/molK)
 ∂T V
1  ∂V 
β= 
coeficiente de expansão térmica(β):
 ; sendo V o volume molar
V  ∂T  P
viscosidade cinemática(υ):
υ=
µ
(em m2/s no SI); sendo µ a viscosidade (dinâmica ou absoluta) e ρ a
ρ
densidade ou massa molar.
calor sensível:
“calor que cedido a um sistema físico é capaz de provocar um
aumento de sua temperatura” ” (Dicionário Houaiss).
de vaporização - λv = HV − H L (HV e HL são respectivamente a entalpia da
Calor latente (λ):
fase gasosa e líquida)
de fusão - λ f = H L − H S (HL e HS são respectivamente a entalpia da fase
líquida e sólida)
Camada Limite hidrodinâmica:região próxima a um corpo submerso em um fluido em escoamento onde
há um gradiente de velocidades.
regime permanente/estacionário ou estado estacionário/permanente: é a condição em que nenhuma
variável se altera com o tempo.
regime/processo/condição/estado transitório/transiente/dinâmico:
é a condição em que pelo menos
uma variável se altera com o tempo
regime pseudo-estacionário ou condição pseudo-estacionária ou estado pseudo-estacionário:
se refere
à condição em que a variação de uma variável com o tempo é muito lenta
Leis de conservação – visão macroscópica:
forma geral:
∂
""
#
ψρ dV = − ∫ ψρ vndA + Ψ
G
∫
∂t VC
SC
sendo,
ψ
...
grandeza a ser conservada
ψ=
...
grandeza específica a ser conservada
...
taxa de geração da grandeza a ser conservada
...
...
o vetor normal à superfície de controle
a velocidade relativa das correntes materiais em relação a um referencial fixo
#
Ψ
G
"
n
"
v
BM
Ψ
m
–
dm
= ∑ m# i − ∑ m# i + m# G
dt i∈E
i∈S
∂
""
ρ dV = − ∫ ρ vndA + ∫ mˆ G dV ; mˆ G kg 3
Geral:
∫
ms
∂t VC
SC
VC
"
"
"
0 = ∑ β j m# j vm, j − ∑ β j m# j vm, j + ∑ Fi ;
VC homogêneo, em e.e.:
VC homogêneo:
(
BQM
–
j∈E
)
vm – velocidade
j∈S
média
escoamento laminar:
Geral:
β=
∂
∂t ∫VC
4
; escoamento turbulento: β = 1.0 (no interior de tubos)
3
"
"
" ""
v ρ dV = − ∫ v ρ ( vn ) dA + ∑ Fi
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
SC
9
Portfolio de:
BEM – transformação entre energias (mecânicas) em e.e.: (energias envolvidas: trabalho de fluido - Wf,
energia cinética - Ec, energia potencial -Ec, trabalho perdido por atrito (WA) que resulta no termo de
perda de carga, trabalho de máquinas - WM)
1 vm2
∆P
∆ + ∆z +
− H A + HM = 0
γ
2g α
escoamento laminar: α = 0.5 ; escoamento turbulento: α = 1.0 (no interior de tubos)
Em termos de carga:
Relações fundamentais da termodinâmica:
Legenda:
H
U
P
T
V
cp
cv
β
...
...
...
...
entalpia específica (J/kg) ou (J/mol)
energia interna específica (J/kg) ou (J/mol)
pressão
temperatura
...
...
...
...
volume molar
calor específico a pressão constante
calor específico a volume constante
coeficiente de expansão térmica
H = U + PV ⇒ dH = dU + PdV + VdP
 ∂H
dH = 
 ∂T
 ∂U
dU = 
 ∂T
∆

 ∂H 
 ∂H 
dT
+
dP
=
c p dT + 



 dP
P
 ∂P T
 ∂P T
∆

 ∂U 
 ∂U 
 ∂U 
 ∂U 
dT
+
dV
=
cv dT + 



 dV ou dU = 
 dT + 
 dP
V
 ∂V T
 ∂V T
 ∂T  P
 ∂P T
A partir das relações acima é possível deduzir que:
  ∂P 

dU = T 
 − P  dV + cV dT
  ∂T  P

  ∂V 
 ∂V  
dU =  −T 
 − P
  dP + cvdT
 ∂P T 
  ∂T  P
 ∂V 
dU = −T 
 dP + c p dT − PdV = −TV β dP + c p dT − PdV
∂
T

P

 ∂V  
dH = V − T 
  dP + cpdT
∂
T

P 

De modo que na prática da engenharia as seguintes simplificações são usuais:
•
Líquidos:
•
Gases ideais:
•
Sólidos:
Observação:
U = H ; dH = cpdT (porque líquidos são normalmente fluidos incompressíveis e
dU = cv dT
dU = c p dT
têm valores de β muito pequenos)
(porque em sólidos
c p ≈ cv )
a determinação experimental de cv é difícil enquanto dados de cp estão disponíveis na
literatura
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
10
Portfolio de:
Exercícios de revisão de balanço de massa:
Exercício 01 (PAFe das turmas 3D, 3E e 3F – FT-I do 1o semestre de 2004):
A figura mostra um tanque cilíndrico aberto de 2m de diâmetro interno, o qual é usado
para estocar água à temperatura ambiente. O tanque pode ser alimentado por duas
correntes com vazões volumétricas F1 (cuja vazão volumétrica é mantida constante em
0.98125 l/s) e F2. O tanque possui uma única corrente de saída, cuja vazão Fs é
controlada. Na tubulação 2 a vazão não é constante.
Vazão da corrente 1:
F1 = 0.98125 0 ≤ t ≤ 20 min
Vazão da corrente 2:
t < 10 min
0
F2 = 
0.0008175t 10 ≤ t ≤ 20 min
Vazão da corrente de saída:
0.98125 0 ≤ t < 10 min
Fs = 
1.20000 10 ≤ t < 20 min
Pede-se:
a) quando não há escoamento pela corrente 2 e a vazão de saída é de 0.98125 l/s,
indicar se o processo se encontra em regime permanente ou transitório.
dm
= m# 1 − m# 3 = ρ ( F1 − F3 ) = 0 (logo processo estacionário)
dt
Observação: a densidade é assumida constante.
b) o escoamento pela corrente 2 se inicia (no instante 10 min) na forma de uma
perturbação do tipo “rampa”, a qual pode ser modelada como: F2 = 0.0008175t ,
sendo t o tempo medido em segundos e F2 dado em (l/s). No instante 10 min a
altura do tanque é de 2.0 m e o engenheiro de processos ajusta a vazão de saída
para 1.2 l/s. Calcule a altura de água no tanque transcorridos mais 10 minutos,
ou seja, a altura de água no instante 20min.
dm
= m# 1 + m# 2 − m# 3
dt
Assumindo densidade constante (água à temperatura constante):
π 2 dh
d
= F1 + F2 − F3 ; d=2m
4
dt
dh 10−3
=
(0.98125 + 0.0008175t − 1.2 )
π
dt
dh
= 10−3 ( −0.069666 + 0.0002604t )
dt
∫
h
2
dh = ∫
20×60
10×60
10−3 ( −0.069666 + 0.0002604t ) dt
0.0002604


h − 2 = 10−3  −0.069666 × ( 20 × 60 − 10 × 60 ) +
12002 − 6002 ) 
(
2


h = 2.136 (m)
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
11
Portfolio de:
Exercício 02:
Qual a vazão volumétrica e velocidade média de escoamento de metano a 150oF e 3 atm
escoando com uma vazão mássica de 1.15ton/dia por uma tubulação de diâmetro interno
de 2.5cm?
Dados da equação de Antoine para o metano: A=-597.84, B=15.2243, C=-7.16, P em
mmHg e T em K.
A
Equação de Antoine: ln P sat = sat
+B
T +C
Determinação do estado físico do metano:
ln (3*760 ) =
−597.84
+ 15.2243 ⇒ T = 86.95K , logo o metano está no estado gasoso!
T − 7.16
Cálculo da densidade do metano (como a pressão é de 3atm, o metano pode ser
considerado como gás ideal):
MMP
16 × 3 × 1.01325 × 105
ρ=
=
= 1727 (g/m3)
RT
8.314 × ( 65.55 + 273.15 )
Cálculo da vazão volumétrica:
F=
1.15 × 1000
= 0.007707 (m3/s)
1.727 × (24 × 3600)
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
12
Portfolio de:
Exercício 04 (P1 da turma 3E – FT-I do 1o semestre de 2004):
A figura a seguir mostra um vasilhame em que água é evaporada. O vapor na camisa de
aquecimento não penetra no vasilhame e fornece a energia suficiente para evaporar a
água. O seguinte modelo foi proposto para calcular a variação do nível de água no
vasilhame.
π d 2 dh
ρl T
= − m# vap
4 dt
sendo,
ρl
... densidade da água líquida avaliada na temperatura do interior do vasilhame
dT
... diâmetro do vasilhame
m# vap ... vazão mássica de saída de vapor
Pede-se:
a-) classificar o processo quanto a ser estacionário, pseudo-estacionário ou
transiente.
Transitório – a massa varia com o tempo e a equação é uma equação diferencial com o
tempo, mostrando que há acúmulo de massa!
b-)
explicar as hipóteses adotadas no modelo apresentado.
Efetuando um VC no interior do vaso temos:
d
( mL + mV ) = −m# vap
dt
Hipótese 1: Como a densidade de gases é muito menor que a de líquidos temos:
d
( mL ) = −m# vap
dt
Hipótese 2: Na mudança de fase, a temperatura é constante, de modo que a densidade
da fase líquida é constante e pode ser colocada para fora do termo diferencial
Hipótese 3: O tanque será assumido cilíndrico
De modo que: ρl
π dT2 dh
= − m# vap
4 dt
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
13
Portfolio de:
Exercícios de revisão de termodinâmica
Exercício 01:
Calcule a entalpia de uma corrente de glicerina a 40oC escoando pelo
espaço anular entre duas tubulações de diâmetros externo de 2.5 cm e
interno de 5cm com uma velocidade de 2.5m/s.
Dados de Incropera & De Witt
T
(K)
273
280
290
ρ
(kg/m3)
1276
1271.9
1265.8
cp
(J/kgK)
2261
2298
2367
ρ
(kg/m3)
1259.9
1253.9
1247.2
T
(K)
300
310
320
cp
(J/kgK)
2427
2490
2564
Representação Gráfica dos Dados Tabelados
Observação: A inspeção visual indica uma dependência linear da densidade e
capacidade calorífica com a temperatura, como também pode ser
observada pelos dados da regressão linear apresentados a seguir.
Regressão Linear dos valores tabelados de densidade e capacidade
calorífica
ρ = 1442.4 − 0.60893T ; (T em K; ρ em kg/m3)
cp = 501.419 + 6.4289T ; (T em K; cp em J/kgK)
T
ρ
(kg/m3)
ρ(ajustado)
(kg/m3)
cp
(J/kgK)
cp(ajustado)
(J/kgK)
(K)
273
280
290
300
310
320
1276
1271.9
1265.8
1259.9
1253.9
1247.2
1276,15
1271,89
1265,80
1259,71
1253,62
1247,53
2261
2298
2367
2427
2490
2564
2256,52
2301,52
2365,81
2430,10
2494,39
2558,68
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
14
Portfolio de:
Cálculo da vazão mássica:
Como o fluido está a 40oC, deve-se obter a densidade a 40oC.
opção 1:
interpolação dos dados tabelados:
320 − 310 1247.2 − 1253.8
=
⇒ ρ = 1251.8 (SI)
ρ − 1253.8
313 − 310
opção 2:
da regressão linear: ρ = 1442.4 − 0.60893 × 313 = 1251.8 (SI)
Observação:
Note a concordância dos dados, o que é característico do
comportamento linear dos dados tabelados!
vazão mássica: m# = 1251.8 ×
π
× ( 0.052 − 0.0252 ) × 2.5 = 4.606 (SI)
4
Cálculo da entalpia específica:
Escolha da referência: como a capacidade calorífica apresenta-se tabelada a partir de
273K, escolhemos como referência o valor de 0oC, uma vez que
este é um valor aceito pela comunidade científica (o correto
seria ainda verificar qual o valor da temperatura de fusão da
glicerina. Por quê?).
Opção 1:
dado o comportamento linear da capacidade calorífica, escolhemos um
valor médio para a capacidade calorífica, obtido como a média dos
valores tabelados, a saber: cp = 2401.2 (J/kgK).
H = 0+ ∫
313
273
2401.2dT = 96048 (J/kg)
Opção 2:
dado o comportamento linear da capacidade calorífica, o cálculo da
integral será feito por trechos, assumindo valores médios em cada
trecho. Reduzimos o número de intervalos considerados, também
devido ao comportamento linear.
290
310
313 2490 + 2512
H = 0 + ∫ 2314dT + ∫ 2428.5dT + ∫
dT = 95411 (J/kg)
273
290
310
2
Observação: Os valores de 2314 e 2428.5 são os valores médios nos intervalos
considerados. O valor de 2512 é o valor da capacidade calorífica a
313K, obtida por interpolação dos dados tabelados.
Opção 3:
cálculo a partir dos valores da regressão linear.
H = 0+ ∫
313
273
(501.419 + 6.4289T ) dT = 95403.5 (J/kg)
# ):
Apresentação dos valores da entalpia da corrente ( H# = mH
opção
entalpia (kW)
erro (obtido em relação ao valor
calculado pelos dados da regressão
linear)
1
442.4
0.6%
2
439.5
0.02%
3
439.4
-//-
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
15
Portfolio de:
Exercício 02:
Calcule a energia interna de 0.2m3 de aço inoxidável AISI 302 a
100oC.
Observações: para sólidos: U ≈ H
Referência para cálculo da entalpia:
0oC
Dados de Incropera & De Witt:
ρ = 8059 (SI)
T=300 (K) : cp=480 (J/kgK)
T=400 (K) : cp=512 (J/kgK)
(também estão disponíveis dados de cp a temperaturas mais altas)
Análise dos valores tabelados:
Observação:
analisando a figura, vemos que o comportamento da capacidade
calorífica com a temperatura não é linear.
Por interpolação: T=100oC : cp=503.4 (SI)
Valor médio da capacidade calorífica para o cálculo da entalpia:
cp=490 (SI)
o
(Como não está disponível o dado de cp a 0 C, uma estimativa possível
é obtida como o valor médio entre 300K e 373K, o que resulta no valor
aproximado de 490 (SI). Um procedimento mais rigoroso seria,
extrapolar o valor de capacidade calorífica para 273K, usando os
valores disponíveis e efetuando uma regressão dos dados tabelados. A
dificuldade é que não mais uma regressão linear é possível, a figura
indica que uma dependência quadrática com a temperatura é possível, e
o ajuste é obtido por mínimos quadrados).
Ajuste quadrático por mínimos quadrados (cálculos foram feitos usando o
programa Matlab):
cp = 372.115 + 0.421348T − 0.000188779T 2 (cp no SI e T em K)
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
16
Portfolio de:
Resultado do ajuste:
T
(K)
300
400
600
800
1000
cp
(J/kgK)
cp(ajustado)
(J/kgK)
480
512
559
585
606
481,53
510,45
556,96
588,37
604,68
Observação:
A 273K o valor de cp pode ser estimado como: 473.1, de modo que
473.1 + 503.4
uma melhor estimativa para o cp médio seria
= 488.2 ,
2
ou seja o valor de 490 é razoável (erro em torno de apenas 0.4%!).
Observação:
Na falta de outros dados de densidade, o valor da densidade será
assumido constante.
Cálculo da entalpia específica:
Opção 1:
H = 0+ ∫
Opção 2:
H = 0+ ∫
100
0
373
273
490dT = 49000 (J/kg)
(372.115 + 0.421348T − 0.000188779T ) dT = 48836
2
(J/kg)
Cálculo da massa:
m = ρV = 1612 (kg)
Valores de energia interna
opção
U (kJ)
1
2
78988
78724
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
erro (em relação à
opção 2)
0.3%
- // -
17
Portfolio de:
Exercício 03:
Calcule a variação de entalpia entre a entrada e saída de um duto de
seção quadrada de 2 cm de lado interno por onde escoa água. A
temperatura da água na entrada do duto é de 15oC e na saída é de 45oC.
Valores tabelados de Incropera & De Witt:
Vˆ
(l/kg)
T
(K)
275
280
285
290
295
300
305
310
315
320
325
330
335
340
cp
(kJ/kgK)
1
1
1
1.001
1.002
1.003
1.005
1.007
1.009
1.011
1.013
1.016
1.018
1.021
4.211
4.198
4.189
4.184
4.181
4.179
4.178
4.178
4.179
4.180
4.182
4.184
4.186
4.188
Observação: note a relativa constância das propriedades tabeladas!
Referência para cálculo da entalpia:
0oC
Interpolando o valor de volume específico a 15oC:
290 − 285 1.001 − 1
=
= 1.0006
290 − 288 1.001 − ρ
Donde a densidade a 15oC é: 999.4 (kg/m3)
Em uma tubulação em operação normal não pode haver acúmulo de massa de modo que
a vazão mássica é constante e pode ser obtida em relação à velocidade média à entrada
do tubo como (note que a velocidade média de escoamento não será constante!):
m# = ρ vm AST = 999.4vm,e 0.022 = 0.3998vm ,e
Cálculo das entalpias específicas na entrada e saída:
H e = 0 + ∫ cpdT
Te
Tref
H s = 0 + ∫ cpdT
Ts
Tref
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
18
Portfolio de:
Donde:
H e − H s = ∫ cpdT = 4.181(15 − 45) = −125.4 (kJ/kg) (foi adotado para a
Te
TS
capacidade calorífica um valor médio dos valores tabelados entre 285K e
320K)
Cálculo da diferença das entalpias das correntes de entrada e saída:
H# e − H# s = m# e H e − m# s H s = m# ( H e − H s ) = −50.13vm (kW)
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
19
Portfolio de:
Exercício 04:
Calcule a variação de entalpia entre a entrada e saída de um tubo de 5
cm de diâmetro interno por onde escoa ar a 2 atm com uma vazão
volumétrica de 19 (l/s). A temperatura do ar na entrada da tubulação é
de 15oC e na saída é de 45oC.
Ar é gás, assim a sua densidade pode ser obtida por uma equação de estado. Como a
pressão da corrente gasosa é de 2 atm, podemos utilizar a equação de estado dos gases
ideais, a saber:
ρ=
MMP 28.8 × 2 × 1.01325 ×105
=
= 2437 (g/m3)
RT
8.314 × 288
Vazão mássica de ar: m# = ρ F = 2.437 × 19 × 10−3 = 0.04631 (kg/s)
Dados de Incropera & De Witt
cp
(kJ/kgK)
T
(K)
150
200
250
300
350
Observação:
1.012
1.007
1.006
1.007
1.009
cp
(kJ/kgK)
T
(K)
400
450
500
550
600
1.014
1.021
1.030
1.040
1.051
o comportamento da capacidade calorífica assume um coportamento
linear com a temperatura acima de 400K, sendo o comportamento da
figura com a temperatura quadrático. Nota-se contudo, uma região em
torno de 250K em que a capacidade calorífica é aproximadamente
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
20
Portfolio de:
constante, assim um valor razoável para cálculos é assumir um valor
constante de 1.007 kJ/kgK.
cp(ajustado)
(kJ/kgK)
T
(K)
150
200
250
300
350
Ajuste dos dados:
1,0111
1,0078
1,0064
1,0070
1,0096
cp(ajustado)
(kJ/kgK)
T
(K)
400
450
500
550
600
1,0141
1,0206
1,0291
1,0395
1,0519
cp = 1.03293 − 0.000204667T + 3.9394 × 10−7 T 2 (T em K, cp em
kJ/kgK)
Cálculo da variação da entalpia específica:
H E − H s = ∫ cpdT
TE
TS
Cálculo através da correlação quadrática: 30.213 (kJ/kg)
Cálculo aproximado:
30.210 (kJ/kg) - (erro de 0.009%)
Variação de entalpia entre E/S: 1.4 (kW)
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
21
Portfolio de:
Exercício 06:
Calcule a entalpia específica das fases líquida e vapor de uma corrente
bifásica saturada de etileno glicol a 470K e 1 atm.
Dados de Incropera & De Witt
Ponto normal de ebulição:
Calor latente de vaporização a 470K:
470K
812 kJ/kg
T
(K)
273
280
290
300
310
320
330
340
350
360
370
373
cp
(J/kgK)
cp(ajustado – regressão linear)
(J/kgK)
2294
2323
2368
2415
2460
2505
2549
2592
2637
2682
2728
2742
2293,11
2324,47
2369,27
2414,07
2458,87
2503,67
2548,47
2593,27
2638,08
2682,88
2727,68
2741,12
Ajuste da capacidade calorífica: cp = 1070.04 + 4.4801T (cp no SI e T em K)
Referência para o cálculo da entalpia: 273K
Cálculo da entalpia específica da fase líquida:
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
22
Portfolio de:
HL = 0 + ∫
470
273
(1070.04 + 4.4801T ) dT = 538.7
(kJ/kg)
Cálculo da entalpia específica da fase vapor:
HV = H L + λvap = 538.7 + 846 = 1385(kJ/kg)
Observação:
O uso de um valor médio para a capacidade calorífica para os dados
tabelados fornece um erro significativo, uma vez que os valores
tabelados são fornecidos até a temperatura de 373K, significativamente
menor que o valor de 470K. Contudo dado o comportamento linear um
outro cálculo aproximado pode ser feito. Pode-se obter a capacidade
calorífica em 470K por interpolação (extrapolação) dos valores e este
valor pode ser mediado com o valor à temperatura de 273K, como
mostram os cálculos a seguir:
Calor especifíco médio dos valores tabelados: 2524.6 (J/kg)
Cálculo da entalpia da fase líquida:
H L = 2524.6 ( 470 − 273) = 499.6
valor não muito razoável (erro de 7%).
Calor específico em 470K:
(kJ/kg),
373 − 370 2742 − 2728
=
⇒ cp470 K = 3194.7
470 − 373
cp − 2742
Cálculo da entalpia da fase líquida:
2294 + 3194.7
HL =
( 470 − 273) = 2744.3 ×197 = 540.6 (kJ/kg) – note a boa
2
aproximação – erro de 0.4% em relação aos valores obtidos da
integração da correlação ajustada, sendo este cálculo bastante mais
simples. Percebe-se assim a importância da análise preliminar dos
dados – para se saber se os dados apresentam um comportamento
linear, quando o procedimento de interpolação e cálculo de médias
é bastante preciso.
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
23
Portfolio de:
Exercício 10:
Pede-se:
a-)
b-)
c-)
Calcular a energia cinética de uma corrente de água líquida a 15oC escoando por
um tubo de 2.5 cm de diâmetro interno com uma velocidade média de 2 m/s.
Calcular a variação de energia potencial entre a entrada e saída de uma corrente de
água líquida a 15oC escoando por um tubo de 2.5 cm de diâmetro interno com uma
velocidade média de 2 m/s, sendo que a saída situa-se a 80m acima da entrada.
Comparar os valores das energias obtidos nos itens a-) e b-) com aqueles obtidos
no exercício 3.
Cálculo da vazão mássica:
Do exercício 3: densidade a 15(oC) : 999.4 (kg/m3)
Vazão mássica: m# = ρ vm AST = 999.4 ×
1
# m2 = 2m# = 1.961 (W)
mv
2α
nas condições do escoamento, este é turbulento, donde não é necessário
se corrigir o valor da energia cinética (i.e., α ≈ 1 ).
Energia cinética:
Observação:
π
× 0.0252 × 2 = 0.9807 (kg/s)
4
Ec =
Variação de energia potencial:
# ∆z = m# × 9.8 × 80 = 784m# = 768.9 (W)
∆Ep = mg
Variação das entalpias (exercício 3):
∆H# = −125.4m# = −200.5 (kW) = -200500 (W)
Observação:
Percebe-se nitidamente que os valores das energias mecânicas são
menores que os da variação da energia térmica!
UPM/EE/DEM/FT-II-5C/ 2004-2S
UPM/EE/DEM&DEE/FT-II-4E/F/ 2004-2S
Apêndices
24