GEOMETRIA ESPACIAL
2017
Tópicos a serem estudados
1) Geometria Espacial de Posição
2) Prismas
3) Pirâmides e troncos de Pirâmide
4) Cilindros
5) Cones e troncos de Cone
6) Esferas e seção da Esfera
7) Poliedros
8) Sólidos de Revolução *
9) Inscrição e Circunscrição de Sólidos *
* apenas EsPCEx
1) Geometria Espacial de Posição
POSTULADOS OU AXIOMAS
1º EXISTÊNCIA:
a) Existem infinitos pontos numa reta, bem como
fora dela;
b) Existem infinitos pontos num plano e também
fora dele;
1) Geometria Espacial de Posição
2º DETERMINAÇÃO:
a) Dois pontos distintos determinam uma única
reta que passa por eles;
b) Três pontos não-colineares determinam um
único plano que passa por eles;
1) Geometria Espacial de Posição
3º INCLUSÃO:
a) Se dois pontos distintos de uma reta pertencem
a um plano, então essa reta está contida nesse
plano;
b) Se dois planos distintos possuem um ponto em
comum, então a intersecção desses planos é uma
reta que passa por esse ponto;
1) Geometria Espacial de Posição
4º PARALELAS
Por um ponto, fora de uma reta dada, passa uma
única paralela à reta dada (postulado de Euclides);
1) Geometria Espacial de Posição
Determinação de um plano
1 - por três pontos não colineares
2 - por uma reta e um ponto fora dela
1) Geometria Espacial de Posição
Determinação de um plano
3 - por duas retas concorrentes
4 - por duas retas paralelas distintas
1) Geometria Espacial de Posição
Exemplo 1
Analise as afirmações, marque V ou F e justifique
suas respostas
a) Três pontos distintos determinam um único
plano.
b) Os vértices de um triângulo são coplanares.
c) Se três pontos são coplanares, então eles são
colineares.
1) Geometria Espacial de Posição
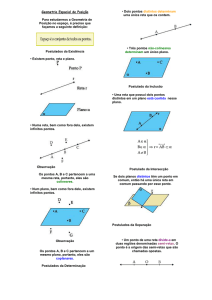
POSIÇÕES RELATIVAS
• Entre duas retas
• De uma reta e um plano
• De dois planos
1) Geometria Espacial de Posição
ENTRE DUAS RETAS
• Coincidentes – quando equivalem a uma única
reta.
• Concorrentes – quando têm um único ponto em
comum.
1) Geometria Espacial de Posição
ENTRE DUAS RETAS
• Paralelas – duas retas distintas são paralelas
quando são coplanares e não tem ponto em
comum.
• Reversas - duas retas distintas são reversas
quando não existe plano que as contenha.
1) Geometria Espacial de Posição
ENTRE RETA E PLANO
• Reta contida no Plano – quando todos os
pontos da reta pertencem ao plano
• Reta e Plano concorrentes (ou secantes) –
quando tem um único ponto em comum
1) Geometria Espacial de Posição
ENTRE RETA E PLANO
• Reta e Plano paralelos – quando não tem
pontos em comum
1) Geometria Espacial de Posição
ENTRE DOIS PLANOS
• Coincidentes – quando equivalem a um mesmo
plano.
• Secantes ou concorrentes – quando são
distintos e têm intersecção não-vazia
1) Geometria Espacial de Posição
ENTRE DOIS PLANOS
• Paralelos – quando não tem ponto em comum
1) Geometria Espacial de Posição
Exercícios:
1)
2)
3)
4)
1) Geometria Espacial de Posição
Exercícios:
5)
1) Geometria Espacial de Posição
Retas ortogonais – duas retas são ditas ortogonais
quando são reversas e a paralela a uma delas,
conduzida por um outro ponto da outra, é
perpendicular a esta.
Se duas retas a e b formam ângulo reto:
Se duas retas a e b formam ângulo reto:
• Sendo reversas, são ortogonais
• Sendo coplanares, são perpendiculares
1) Geometria Espacial de Posição
Reta e Plano Perpendiculares – uma reta
concorrente com um plano, num ponto O, é
perpendicular ao plano quando é perpendicular a
todas as retas do plano que passam por O.
1) Geometria Espacial de Posição
Planos Perpendiculares – quando um deles
contém uma reta perpendicular ao outro.