1 - UNESP

1. Postulados
A geometria em Euclides o seu construtor inicial, ou melhor, foi ele o primeiro a
organizar a geometria de forma axiomática.
Axiomas, ou postulados, são proposições aceitas como verdadeiras sem
demonstração e que servem de base para o desenvolvimento de uma teoria.
Os conceitos primitivos, como ponto, reta e plano, não tem definição, mas podemos
representá-los graficamente:
a) Ponto
b) Reta
c) Plano
Observação: Espaço é o conjunto de todos os pontos.
A notação usada por Hilbert (1862-1943), e normalmente adotada por nós, é a seguinte:
 Os pontos são indicados por letras maiúsculas (A, B, C etc.).
 As retas são indicadas por letras minúsculas (r, s, t etc.).
 Os planos são indicados por letras gregas (  ,  ,  etc.).
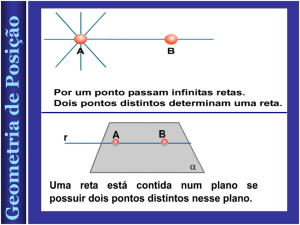
Postulado 1 : : Dois pontos distintos determinam uma única reta.
Exemplo:
1

r  PQ( P  Q)
Postulado 2 : Existem infinitos pontos numa reta e fora dela também.
Exemplo:
s
 A  s; B  s; C  s

D  s; E  s; F  s
Postulados 3 : : Três pontos não-alinhados determinam um único plano.
Exemplo:
2
Postulado 4 : Existem infinitos pontos num plano e fora dele também.
Exemplo:
A ; B ;C 

E   ; F   ; G  
Postulado 5 : Se dois pontos distintos de uma reta pertencem a um plano, então essa reta
está contida nesse plano.
Exemplo:
3
A B


A  r ; B  r r  
A   ; B   
Postulado 6 : Por um ponto, fora de uma reta dada, passa uma única paralela à reta dada
(Postulado de Euclides).
Exemplo:
Postulado 7 : Se dois planos distintos possuem um ponto em comum, então, a intersecção
desses planos é uma reta que passa por esse ponto.
Exemplo:
Exercício
Assinale V (verdadeiro) ou F (falso):
a) Duas retas distintas podem ter um único ponto em comum.
b) Por dois pontos pode passar uma reta.
c) Em toda reta existem pelo menos dois pontos.
d) Por dois pontos distintos passam duas retas distintas.
e) Dada uma reta, existe pelo menos um ponto fora dela.
f) Dado um plano, existe pelo menos um ponto fora dele.
g) Existe um único plano que passa por dois pontos distintos.
4
h)
i)
j)
k)
Um triângulo estará sempre contido em um plano
Um plano contém infinitas retas.
Uma reta está contida num plano se tiver um ponto em comum com esse plano.
Se dois planos distintos possuem um ponto em comum, então possuem outro ponto
em comum distinto do primeiro.
l) A paralela a uma reta por um ponto é única.
2. Posições relativas de duas retas no espaço
Considerando duas retas distintas s e t, podemos classificá-las como coplanares, se
estiverem contidas no mesmo plano, e não-coplanares ou reversas, caso não exista um
plano que as contenha.
As retas coplanares podem ser concorrentes, paralelas não-coincidentes, paralelas
coincidentes, perpendiculares ou ortogonais.
Concorrentes: duas retas são concorrentes quando se interceoptam em um único
ponto.
Exemplo: As retas s e r são concorrentes, pois se interceptam num único ponto P.
r s  P
Paralelas não-coincidentes: duas retas são paralelas não-coincidentes quando são
coplanares e de intersecção vazia.
Exemplo:
s 
r 
sr  
s e r são paralelas
5
Paralelas coincidentes: duas retas são paralelas coincidentes quando possuem todos
os pontos em comum.
Exemplo: As retas s e r são paralelas coincidentes, pois apresentam todos os pontos
em comum.
Retas perpendiculares: se duas retas são coplanares e formam um ângulo reto, então
são chamadas de perpendiculares.
Exemplo: As retas s e r estão no plano  , se interceptam em P e formam um ângulo
de 90°. Portanto, são perpendiculares (s  r) .
s 
r 
s  r  {P}
s 
(s e r são perpendicuçares).
Não-coplanares ou reversas: duas retas são reversas quando não há plano algum
que as contenha.
Exemplo: As retas s e r são reversas, pois não existe um plano que as contenha.
6
s 
r 
s  r  0
sr
Retas ortogonais: se duas retas são reversas e se existem uma terceira reta
perpendicular a uma delas e paralela à outra, dizemos que as duas primeiras retas
formam um ângulo reto. Retas reversas que formam um ângulo reto são chamadas de
retas ortogonais.
Exemplo: As retas r e t da figura são ortogonais (t  r), pois traçando por um ponto
P de t , reta s paralela a t, observamos que t e r são perpendiculares.
t 

s   , s // t 
r t
t  r  {P} 
t  r , r   
Exercícios:
1. Identificar no cubo:
7
a)
b)
c)
d)
e)
f)
dois pares de retas concorrentes
dois pares de retas paralelas não-coincidentes
dois pares de retas coplanares
dois pares de retas reversas
um par de retas perpendiculares
um par de retas ortogonais
2. Assinale V (verdadeiro) ou F (falso):
a)
b)
c)
d)
e)
f)
g)
h)
i)
Se duas retas são distintas e paralelas, então são coplanares.
Duas retas distintas ou são reversas ou são paralelas ou são concorrentes.
Duas retas concorrentes são coplanares somente quando forem perpendiculares.
Duas retas distintas que têm um ponto em comum são coplanares.
Duas retas paralelas a uma terceira são paralelas entre si.
Se duas retas são reversas, podem ter um ponto em comum.
Se duas retas r e t são reversas, então r t  0 .
Diante da afirmação r t  0 , podemos dizer que r e s são reversas.
Se duas retas r e t são paralelas coincidentes, então a afirmação r = t é válida.
3. (Fesp) Sejam a e b duas retas distintas de um plano  . Suponhamos que a e b
não sejam paralelas entre si, logo, a e b têm em comum um único ponto M.
Nesse caso, devemos escrever:
a) a  b  M
b) a  b  M
c) a b  0
d) a  b  {M }
e) n.d.a.
8
3. Posições relativas de uma reta e um plano
Uma reta e um plano podem ocupar no espaço as seguintes posições relativas.
A reta está contida no plano: uma reta está contida num plano se ela tem dois
pontos distintos nesse plano, conforme o postulado 5.
Exemplo:
A  s, A  
B  s, B  
s    s   s
A reta é paralela ao plano: uma reta é paralela a um plano se ela não tem nenhum
ponto em comum com esse plano.
Exemplo: Se uma reta r e um plano  não têm ponto em comum, então a reta r é
paralela a uma reta t contida no plano
 ; portanto r //
, ou seja s     
A reta é concorrente com o plano: uma reta é concorrente com um plano se a sua
intersecção com o plano determinar um único ponto.
Exemplo: Dizemos que a reta r “fura” o plano  ou que r e  são concorrentes em P
quando r    P .
9
r   P
Reta e plano perpendiculares: uma reta s é perpendicular a um plano  se é
concorrentes com o plano e perpendicular a todas as retas do plano que passam pelo
ponto de intersecção.
Exemplo: Uma reta r é perpendicular a um plano  se, e somente se, r é
perpendicular a todas as retas de  que passam pelo ponto de intersecção de r e  .
r    P



 P  t , P  s, P  u , P  r   r  
r  t , r  s, r  u



Do perpendicularismo entre reta e plano decorrem propriedades como:
1ª propriedade: se uma reta e um plano são perpendiculares então essa reta forma
um ângulo reto com qualquer reta do plano.
Exemplo: Seja a reta t e u (quaisquer) pertencente ao plano  e uma reta r
perpendicular a reta t.
10
t   


u     r  t e r  u
r   


2ª propriedade: uma reta e um plano são perpendiculares quando essa reta é
perpendicular a duas retas concorrentes em seu traço e contidas no plano.
Exemplo:
Exercícios
1º Desenhe as situações indicadas e diga quais das afirmações são falsas?
a) Se uma reta s não está contida no plano  , mas é paralela a uma reta t contida em  ,
então s é paralela a  .
b) Por um ponto P fora de um plano  passa uma única reta paralela ao plano  .
c) Se P é um ponto pertencente ao plano  , então infinitas retas contidas em  passam
por P.
d) Se duas retas concorrentes s e t pertencem a um plano  e são paralelas a um plano
 , então  e  são paralelos.
e) Se uma reta r é perpendicular a apenas uma reta do plano  , ela é necessariamente
perpendicular ao plano.
f) Se uma reta s é perpendicular a um plano  , qualquer reta paralela a s é perpendicular
ao plano.
11
 , qualquer plano paralelo a 
g) Se uma reta s é perpendicular ao plano
à reta s.
é perpendicular
2º) Num plano  há duas retas r ( A,B  r ) e s (C,D  s ) concorrentes num ponto O. Fora
de  há um ponto P. Qual a interseção dos planos  formado pelos três pontos nãocolineares (A,B,P) e o plano

formado pelos outros três pontos não-colineares (C,D,P)?
3º) Um ponto P é o traço de uma reta r num plano
passa por r, o que ocorre com a interseção
.
Se

é um plano qualquer que
  t ?
4. Posições relativas de dois planos no espaço
Dois planos distintos podem ocupar no espaço as seguintes posições relativas:
Paralelos coincidentes: dois planos são paralelos coincidentes quando têm todos os
pontos em comum.
Exemplo: Dados dois planos paralelos coincidentes  e  .
 
Paralelos distintos: dois planos são paralelos distintos quando não têm pontos em
comum.
Exemplo: Dois planos são paralelos quando sua intersecção é vazia.
12
   
Secantes ou concorrentes: dois planos são secantes ou concorrentes quando têm
apenas uma reta em comum.
Exemplo: Dois planos,  e  , são concorrentes quando sua intersecção é uma
única reta.
   r
Perpendiculares: dois planos concorrentes são perpendiculares quando um deles
contém uma reta perpendicular ao outro.
Exemplo: Dois planos,  e  , são perpendiculares se, e somente se, existe uma
reta de um deles que é perpendicular ao outro:
Seja uma reta s contida no plano  e s é perpendicular ao plano  . No plano 
está contido a reta r que é perpendicular ao plano  . Portando temos que o plano
 perpendicular a  .
13
    t , r , t   , r   e r  t
Do perpendicularismo entre planos decorrem propriedades como:
Se uma reta é perpendicular a um plano, por ela passam infinitos planos, também
perpendiculares ao plano inicial.
Exemplo: Dado o plano  (verde) e a reta r   , temos: (  plano amarelo e 
plano laranja).




 
, portanto,   
r  , s  
s 
, portanto   
s 
Exercícios:
1º) Assinalar V (verdadeiro) ou F (falso):
a) Se o plano  contém duas retas concorrentes que são paralelas ao plano  ,
então  é paralelo a  .
14
b) Em dois planos paralelos todas as retas de um plano são paralelas ao outro.
c) Os planos  e  somente serão paralelos se      .
d) Para que dois planos sejam paralelos é suficiente que duas retas distintas
contidas num deles sejam paralelas ao outro.
e) Por uma reta s perpendicular a um plano  passa um único plano perpendicular
a .
2º) (UNESP) Se  é um plano e b uma reta não perpendicular a  , então:
a)
b)
c)
d)
e)
não existe plano passando por b perpendicular a  .
Existem, no mínimo, dois planos passando por b e perpendicular a  .
Existe um e um só plano passando por b e perpendicular a  .
Existe uma infinidade de planos passando por b e perpendicular a  .
Todo plano passando por b não é perpendicular a  .
3º) Se dois planos paralelos interceptam um terceiro, então as interseções são
paralelas.
Observações do livro do Xavier e Barreto.
Segundo a observação que o Elon faz na pg 164.
“Na nossa opinião, não é apropriado apresentar, no 2º grau, uma teoria axiomática
formal para a Geometria Espacial. Mas é importante estabelecer as regras básicas do
jogo, introduzindo as entidades fundamentais (ponto, reta, plano, espaço) como
noções primitivas e apresentando alguns axiomas como propriedade a serem aceitas
sem demonstração.”
Este livro traz de forma simples o tema de Geometria Espacial, fazendo
anteriormente uma recordação da Geometria Plana.
Bibliografia:
BARRETO,B.F., SILVA,C.X.; Matemática Aula por Aula, Editora FTD, São Paulo,
2.005.
15