Relatório

PONTIFÍCIA UNIVERSIDADE CATÓLICA DO PARANÁ
ESCOLA POLITÉCNICA
ENGENHARIA ELÉTRICA - TELECOMUNICAÇÕES
CAIO MARCELO DE MIRANDA
DIDIER KAZADI MPOLESHA
ENLACES RESSONANTES MAGNETICAMENTE ACOPLADOS PARA FINS DE
TRANSFERÊNCIA DE ENERGIA
CURITIBA
2014
2
CAIO MARCELO DE MIRANDA
DIDIER KAZADI MPOLESHA
ENLACES RESSONANTES MAGNETICAMENTE ACOPLADOS PARA FINS DE
TRANSFERÊNCIA DE ENERGIA
Trabalho de Conclusão de Curso
Engenharia Elétrica – Telecomunicações
apresentado
ao
departamento
de
Engenharia Elétrica da Escola Politécnica
da Pontifícia Universidade Católica do
Paraná, como requisito parcial à obtenção
do título de Engenheiro Eletricista.
Orientador: Prof. Dr. Munir Antonio Gariba
CURITIBA
2014
3
CAIO MARCELO DE MIRANDA
DIDIER KAZADI MPOLESHA
ENLACES RESSONANTES MAGNETICAMENTE ACOPLADOS PARA FINS DE
TRANSFERÊNCIA DE ENERGIA
Trabalho de Conclusão de Curso Engenharia Elétrica – Telecomunicações
apresentado ao departamento de Engenharia Elétrica da Escola Politécnica da
Pontifícia Universidade Católica do Paraná, como requisito parcial à obtenção do
título de Engenheiro Eletricista.
COMISSÃO EXAMINADORA
_____________________________________
_____________________________________
_____________________________________
Curitiba, ____ de ________ de 2014.
4
RESUMO
Atualmente muita atenção acadêmica e industrial vem sendo dada a transmissão de
energia sem fio via enlaces ressonantes magneticamente acoplados. Com esta
técnica
pode-se
alcançar médias
distâncias
em
enlaces que
devido
as
características magnéticas sofrem pouca interferência de objetos externos, sendo
bastante interessantes, portanto, para aplicações em ambientes fechados de
escritórios, residências e fábricas. Neste trabalho mostra-se uma revisão desta
técnica baseada em artigos da literatura. São realizados ensaios e simulações para
comprovar a teoria apresentada discutindo a eficiência e transferência relativa de
potência. Por fim são realizados experimentos aonde foi acesa uma lâmpada de 25
Watts, sendo as eficiências de transmissão discutidas.
Palavras-chave—
Ressonância;
Transferência de Energia sem Fio;
Bobina;
Acoplamento
Magnético;
Enlace;
5
ABSTRACT
Currently quite academic and industrial attention have been given to power
transmission via wireless resonant links magnetically coupled. With this technique it
is possible to achieve medium distances on links that due to the magnetic
characteristics have little interference from external objects, and is therefore very
interesting for applications in closed environments of offices, residences and
factories. In this work it is shown a review about this technique based on published
articles. Tests and Simulations are done to prove the presented theory, discussing
the relative efficiency and relative power transfer. Finally, experiments where a 25
Watts light bulb was lighted are shown, being the efficiency and relative
power
transfer discussed.
Key-words— Resonance, Coil, Magnetic Coupling, Link, Wireless Energy Transfer;
6
LISTA DE ILUSTRAÇÕES
Figura 1 - Esquema utilizado .....................................................................................13
Figura 2 - Grupo MIT .................................................................................................14
Figura 3 - Esquema de transmissão...........................................................................15
Figura 4 - Modelo de transformador...........................................................................16
Figura 5 - Circuito elétrico...... ...................................................................................18
Figura 6 - Circuito equivalente....................................................................................20
Figura 7 - Representação de um sistema de 2 bobinas.............................................22
Figura 8 - Representação de um sistema de 4 bobinas.............................................24
Figura 9 - Níveis de referência para exposição a campos elétricos...........................34
Figura 10 - Níveis de referência para exposição a campos magnéticos....................35
Figura 11 - Coeficiente de acoplamento medido........................................................37
Figura12 - Setup utilizado nos testes.........................................................................38
Figura 13 - Comparação entre eficiência e transferência relativa..............................39
Figura 14 - Efeito de diferentes cargas na transferência relativa de potência......... 40
Figura 15 - Efeito de diferentes cargas na eficiência.................................................40
Figura 16. Comparação entre eficiência e transferência relativa...............................41
Figura 17. Comparação entre eficiência e transferência relativa...............................42
Figura 18. Efeito de diferentes cargas na transferência relativa................................42
Figura 19. Efeito de diferentes cargas na eficiência..................................................43
Figura 20. Sistema completo utilizado nos testes de potência..................................44
Figura 21. Eficiência e transferência relativa de potência simuladas........................45
Figura 22. Bobinas 1 e 2 a 8 cm de distância. Eficiência de 25 %.............................46
Figura 23. Bobinas 1 e 2 a 8 cm de distância. Eficiência de 9 %...............................46
Figura 24. Eficiência e transferência relativa de potência simuladas........................47
Figura 25. Bobinas 1 e 2 a 15 cm, 3 e 4 a 8 cm, e 2 e 3 a 30 cm..............................48
Figura 26. Bobinas 1 e 2 a 15 cm, 3 e 4 a 8 cm, e 2 e 3 a 40 cm..............................49
7
SUMÁRIO
1 INTRODUÇÃO ........................................................................................................ 7
1.1 OBJETIVOS ......................................................................................................... 8
1.2.1 Objetivo Geral ................................................................................................. 8
1.2.2 Objetivos Específicos..................................................................................... 8
2 REVISÃO TEÓRICA ............................................................................................... 9
2.1 Enlaces com bobinas autorressonantes ........................................................ 15
2.1.1 Descrição do sistema..................................................................................... 15
2.1.2 Bobina de potência e transmissora .............................................................. 16
2.1.3 Esquema completo (4 bobinas) .................................................................... 19
2.2 Enlaces ressonantes com elementos concentrados (LC) ............................. 21
2.2.1 Sistemas com 2 bobinas................................................................................ 22
2.2.2 Sistemas com 4 bobinas................................................................................ 24
2.3 Trabalhos recentes ........................................................................................... 28
2.4 Normas para exposição a campos .................................................................. 28
2.4.1 Efeitos causados pelos campos ................................................................... 28
2.4.1.1 Mecanismos de acoplamento ..................................................................... 29
2.4.1.2 Acoplamento a campos eletricos de baixa frequência ........................... 29
2.4.1.3 Acoplamento a campos magnéticos de baixa frequência ...................... 29
2.4.1.4 Absorção da energia de campos eletromagnéticos ................................. 30
2.4.2 Limites para exposição ocupacional ............................................................ 31
2.4.3 Níveis de referência........................................................................................ 33
3 RESULTADOS ....................................................................................................... 35
3.1 Sistema com 2 bobinas..................................................................................... 38
3.2 Sistema com 4 bobinas..................................................................................... 40
3.3 Testes com alta potência .................................................................................. 43
3.3.1 Sistema com 2 bobinas.................................................................................. 44
3.3.2 Sistema com 4 bobinas.................................................................................. 46
4 DISCUSSÃO .......................................................................................................... 49
AGRADECIMENTOS ............................................................................................... 51
REFERÊNCIAS ......................................................................................................... 52
8
INTRODUÇÃO
A transmissão de energia sem fio, apesar de se tratar de um tema bastante
atual, já havia sido idealizada e experimentada por Nikola Tesla no fim do século XIX
(TESLA, 1891). Tesla empreendeu esforços gigantescos neste sentido, chegando
inclusive a propor um sistema mundial de transmissão de energia sem fio antes que
o sistema de distribuição de energia a cabo estivesse totalmente desenvolvido
(TESLA, 1900). Dentre alguns feitos notáveis com esta técnica, Tesla chegou a
acender várias lâmpadas a grandes distâncias, bem como a acionar motores, e
ainda afirmou ter transmitido correntes para o outro lado do globo utilizando a terra
como condutor (TESLA, 1900). Apesar de teoricamente o sistema de Tesla ser
bastante promissor, este não foi levado a diante na época, e o sistema de
transmissão de energia cabeado se desenvolveu ao ponto de atualmente atender
grande parte da população mundial. Neste sentido, a transmissão de energia sem fio
em larga escala, à grandes distâncias, em princípio não se faz necessária nos dias
de hoje. Atualmente pode-se considerar como grande desafio a transmissão de
energia à médias e curtas distâncias, visando carregar dispositivos eletrônicos em
residências, estações de trabalho e fábricas. Sendo assim, a utilização de links
ressonantes magneticamente acoplados apresenta-se como uma promissora
solução. Estes links ressonantes quando comparados aos métodos de indução
tradicionais, possuem a vantagem de aumentar consideravelmente o alcance do link,
isto é, algumas vezes a dimensão das bobinas envolvidas.
9
1.1 OBJETIVOS
1.1.1 Objetivo Geral
Apresentar a técnica da transmissão de energia sem fio via enlaces
ressonantes magneticamente acoplados, e realizar a transferência de energia a uma
carga avaliando a eficiência e transferência relativa de potência.
1.1.2 Objetivos Específicos
a) realizar uma revisão dos principais conceitos que envolvem a técnica;
b) equacionar o enlace ressonante;
c) realizar e avaliar a transferência de potência e eficiência;
d) realizar simulações para comparação.
10
2 REVISÃO TEÓRICA
O conceito de que dois objetos que possuem a mesma frequência de
ressonância natural, quando oscilando nesta frequência, tendem a trocar energia
entre si de maneira mais eficiente do que quando vibrando em outra frequência, é
intuitivo em primeiro momento. Também não é novidade de que este tipo de
acoplamento ressonante é extensivamente utilizado para alimentação de sensores
biomédicos passivos (KO; LIANG; FUNG, 1977) e em RFID’s. Porém, um grande
destaque foi dado a esta técnica com o intuito de transferir energia sem fio quando
em 2007 um grupo do MIT publicou alguns artigos formalizando matematicamente e
fisicamente este conceito e provando as suas vantagens (KURS et. al., 2007). Os
autores também conseguiram acender uma lâmpada de 60 W com eficiência de 15%
a 2 metros de distância (as bobinas utilizados possuíam 60 cm de diâmetro). Deste
trabalho nasceu uma empresa denominada Witricity com fins de desenvolver
aplicações industriais utilizando a técnica proposta (WITRICITY, 2014). Deve-se
enfatizar que, diferentemente do sistema proposto por Nikola Tesla onde grandes
intensidades de campos elétricos estavam envolvidas (e grandes distâncias eram
alcançadas), a técnica aqui estudada utiliza apenas o acoplamento magnético no
chamado campo próximo aos objetos, o quê é mais apropriado para aplicações em
fábricas, escritórios e residências.
O enfoque aqui é dado à transferência de energia entre duas bobinas com
núcleo de ar, já que este é o tipo de enlace mais comumente utilizado na prática.
Estas devem possuir dimensões apropriadas para quê trabalhem no regime de
elementos concentrados (“lumped”) onde as dimensões da bobina são muito
menores do quê o comprimento de onda (λ). Nestas situações a bobina pode ser
modelada como possuindo uma indutância (L), capacitância (C) e resistência (R)
concentradas equivalentes. Trabalhar neste regime evita que parte da energia do
enlace seja perdida por irradiação, como ocorre no caso de solenoides relativamente
longos onde a corrente não é uniforme ao longo do mesmo, e existem ressonâncias
por ondas estacionárias presentes (CORUM; CORUM, 2001). Um capacitor externo
11
conectado em paralelo com a bobina também pode ser utilizado para aumentar o
valor da capacitância e baixar a frequência de ressonância (𝑓𝑜 ). A frequência de
ressonância (𝑓𝑜 ) das bobinas do enlace, deve-se então à indutância e capacitância
equivalentes, sendo dada por
𝑓𝑜 =
1
2𝜋√𝐿𝐶
(1)
É importante que as fo’s das bobinas envolvidas sejam iguais ou então muito
próximas, visando máxima transferência de energia. Estes circuitos acoplados
podem ser descritos pela teoria dos regimes acoplados (HAUS, 1984) sendo esta a
abordagem utilizada nas principais referências deste trabalho (KURS et. al., 2007) e
(KARALIS; JOANNOPOULOS; SOLJAČIĆ, 2007). Nesta teoria, define-se como
figura de mérito (fdm) de toda a análise a relação,
𝑓𝑑𝑚 =
к
√Г1 Г2
(2)
onde к é a taxa de acoplamento, Г1 e Г2 representam as perdas na bobina 1 e 2,
respectivamente. A taxa de acoplamento pode ser interpretada como uma medida
de quão rápido as bobinas trocam energia, sendo dada por,
к=
𝜔𝑀
2√𝐿1 𝐿2
(3)
onde ω é a frequência angular, M é a indutância mútua, L1 é a indutância da bobina
1 e L2 a indutância da bobina 2. Reconhece-se o termo M/√(L1L2 ) como o
coeficiente de acoplamento k da teoria de circuitos. As perdas, representadas por Г,
devem-se a perdas ôhmicas (absorção) e por irradiação e representam o quão
rápido a energia é perdida. As perdas ôhmicas ocorrem principalmente nos
enrolamentos das bobinas, bem como em objetos estranhos próximos ao enlace. As
perdas por irradiação podem ocorrer devido à irradiação individual nas bobinas, bem
como à energia que pode ser espalhada por objetos estranhos próximos ao enlace.
Visto que a energia perdida é determinante na eficiência da transferência de
energia (equação 2), o fator de qualidade, ou fator de mérito das bobinas (𝑄) é um
parâmetro de grande importância no projeto.
O fator de qualidade é definido como a relação
𝑄=
ou ainda
2𝜋(𝑒𝑛𝑒𝑟𝑔𝑖𝑎 𝑎𝑟𝑚𝑎𝑧𝑒𝑛𝑎𝑑𝑎)
𝑒𝑛𝑒𝑟𝑔𝑖𝑎 𝑝𝑒𝑟𝑑𝑖𝑑𝑎 𝑝𝑜𝑟 𝑐𝑖𝑐𝑙𝑜
(4)
12
𝑄=
𝜔𝑜 (𝑒𝑛𝑒𝑟𝑔𝑖𝑎 𝑎𝑟𝑚𝑎𝑧𝑒𝑛𝑎𝑑𝑎)
𝑝𝑒𝑟𝑑𝑎 𝑚é𝑑𝑖𝑎 𝑑𝑒 𝑝𝑜𝑡ê𝑛𝑐𝑖𝑎
=
𝜔𝑜 𝑈
𝑊
(5)
onde ωo é a frequência angular na ressonância. As perdas podem ser expressas por
(RAMO; WHINNERY; DUZER, 1965)
Г=
𝑊
(6)
2𝑈
Desta maneira 𝑄 também pode ser expresso como,
𝑓𝑑𝑚 =
к
√Г1 Г2
(7)
Portanto, um alto valor de 𝑄 indica baixa perda de energia, e consequentemente
maior é a figura de mérito da análise definida na equação (2).
Nota-se, portanto, que existe uma relação de compromisso com a escolha da
frequência de operação, uma vez que da equação (3) uma maior frequência acarreta
maior taxa de acoplamento, por outro lado, altas frequências acarretam em
irradiação de energia na forma de ondas eletromagnéticas, além do aumento do
efeito pelicular, o quê acarreta em um aumento das perdas. Neste sentido segue a
afirmação feita em (KARALIS; JOANNOPOULOS; SOLJAČIĆ, 2007): “Ao ajustar a
capacitância e portanto a frequência de ressonância, o 𝑄 total se torna máximo para
certa frequência ótima determinada pelos parâmetros do enrolamento: em baixas
frequências é dominado por perdas ôhmicas e em altas frequências por irradiação.”
Desta maneira, considerando que as principais perdas ocorrem nas bobinas (o quê é
geralmente verdade), pode-se definir um 𝑄𝑜ℎ𝑚 devido a perdas ôhmicas e um 𝑄𝑖𝑟𝑟
devido a irradiação como sendo (KARALIS; JOANNOPOULOS; SOLJAČIĆ, 2007),
𝑄𝑜ℎ𝑚 =
𝑄𝑖𝑟𝑟 =
𝜔𝐿
𝑅𝑜ℎ𝑚
𝜔𝐿
𝑅𝑖𝑟𝑟
(8)
(9)
onde 𝑅𝑜ℎ𝑚 e 𝑅𝑖𝑟𝑟 são as resistências ôhmicas e de irradiação, respectivamente
(pode-se demonstrar que as equações (8) e (9) derivam da equação (4) (RAMO;
WHINNERY; DUZER, 1965). Nota-se novamente quê esta análise trata de uma
aplicação em campo próximo, já que em campos distantes e em antenas é desejável
uma grande resistência de irradiação e consequente maior largura de banda para
tornar a antena eficiente.
Tendo em vista aumentar a 𝑓𝑑𝑚 da análise, uma estratégia pode ser a de
aumentar o valor de L ou C. Desta maneira aumenta-se a energia armazenada na
13
indutância ou na capacitância. Sabe-se que na ressonância a energia armazenada
no circuito é a energia máxima armazenada na capacitância, ou a energia máxima
armazenada na indutância, já que a energia é armazenada no campo magnético e
no campo elétrico oscilando de um ao outro periodicamente. Isto é, em condições de
ressonância, a energia armazenada na indutância ou na capacitância são iguais
(RAMO; WHINNERY; DUZER, 1965). Sendo assim, maximizando L ou C implica no
aumento da energia armazenada no circuito como um todo, e por fim aumenta-se 𝑄.
Portanto, isto pode indicar que maximizar um parâmetro ou outro, e não ambos
simultaneamente, é preferível já que o aumento da energia armazenada no circuito
em ressonância é igual àquela armazenada individualmente em L ou C.
Considerando que as perdas são funções das dimensões dos componentes, ao
aumentar o valor dos dois parâmetros, teoricamente aumenta-se também as perdas
em ambos os componentes.
O alcance dos enlaces aqui tratados são considerados de médias distâncias,
isto é, algumas vezes a dimensão característica da bobina (geralmente o raio ou o
comprimento longitudinal). A figura de mérito têm um papel importante no alcance do
enlace; quando esta é maximizada, consegue-se transmitir a energia a maiores
distâncias de maneira eficiente. O alcance ou extensão do campo próximo é
geralmente determinado por λ, isto é, maiores comprimentos de onda resultam em
maior alcance, porém não necessariamente indicam mais eficiência, como foi
mencionado no caso da escolha de uma frequência ótima de operação. Para
aplicações reais, uma estratégia pode ser a de aumentar as dimensões da bobina
primária (fonte) mantendo as dimensões da bobina secundária (acoplada a um
dispositivo móvel por exemplo) fixas, desta maneira não se limita o alcance do
enlace apenas ao comprimento de onda. Neste caso, considera-se que a bobina
primária é estacionária, e possui menos restrições em relação a sua dimensão,
enquanto que a bobina secundária pode ser móvel, e por estar acoplada a um
dispositivo possui mais restrições em relação a sua dimensão (KARALIS;
JOANNOPOULOS; SOLJAČIĆ, 2007).
A influência de objetos estranhos próximos ao enlace ressonante pode
resultar em perdas adicionais (absorção, espalhamento, etc.) alterando o Q ou até
mesmo reforçar ou cancelar o sinal devido a interferência entre os campos. A
influência destes objetos também pode causar um desvio na frequência (ωo+Δω).
14
Este desvio pode ser corrigido usando uma realimentação e alterando o valor de L
ou C do conjunto. Uma das vantagens da técnica em análise é de que as perdas por
absorção em objetos próximos são bastante minimizadas uma vez que se trabalha
com o acoplamento por campo magnético e a maioria dos objetos de uso diário (com
µ próximo ao do espaço livre) não reage a este (KARALIS; JOANNOPOULOS;
SOLJAČIĆ, 2007).
A Figura 1 mostra o ensaio realizado pelo grupo do MIT. Neste ensaio, foi
utilizado um oscilador Collpits de alta potência conectado a um loop (1 volta com 25
cm de raio), o qual é indutivamente acoplado à bobina transmissora (L1) que
ressona na mesma frequência da bobina receptora (L2). A bobina receptora é
também indutivamente acoplada a uma bobina de poucas voltas, a qual é conectada
a uma lâmpada de 60 W. As bobinas transmissora e receptora possuem raio de 30
cm, comprimento de 20 cm, fio de cobre de diâmetro 6 mm e 5.25 voltas. Neste
experimento os autores não utilizaram um capacitor conectado à bobina e portanto a
frequência em que estas ressonam é a frequência de autorressonância, que se deve
a capacitância intrínseca da bobina e da sua indutância total. Esta frequência neste
teste é de 9,9 MHz. Os autores citam que ao invés de acoplar indutivamente o
circuito excitador e a carga, estes poderiam ser conectados por fios às bobinas L1 e
L2.
Figura 1. Esquema utilizado. A esquerda tem-se o circuito oscilador conectado a uma loop (L1)
indutivamente acoplado a bobina transmissora (L2) que por sua vez ressona na mesma frequência de
ressonância natural da bobina receptora (L3), esta é acoplada indutivamente a uma bobina de poucas
voltas (L4) que conecta-se a uma lâmpada de 60 W.
Fonte: (MOFFAT, 2009).
15
Figura 2 – Grupo do MIT posicionado entre o enlace ressonante, mostrando a relativa
imunidade do sistema a presença humana.
Fonte: (MOFFAT, 2009)
2.1 ENLACES COM BOBINAS AUTORRESSONANTES
Cheon et al. (2011) apresentam uma abordagem do esquema de transmissão
de energia com bobinas autorressonantes (tal como utilizado pelo grupo MIT), do
ponto de vista da teoria de circuitos elétricos, bastante apropriada a esse estudo. A
seguir, será mostrado o método utilizado pelos autores.
2.1.1 DESCRIÇÃO DO SISTEMA
A Figura 3 apresenta um resumo do esquema de transferência completo, com
4 bobinas. Estas são denominadas bobina de potência, transmissora, receptora e de
carga. Entre estas bobinas existem os coeficientes de acoplamento, denominados
Kpt, Ktr, Krc, Kpr, Ktc e Kpc (os índices p,t,r,c correspondem as bobinas de potência,
transmissora, receptora e de carga, respectivamente). Os coeficientes de
16
acoplamento entre bobinas não adjacentes, ou inter-acoplamentos Kpr, Ktc e Kpc,
são desprezados.
Figura 3 – Esquema de transmissão com as bobinas de potência, transmissora, receptora e de
carga. Kpt, Ktr, Krc, Kpr, Ktc e Kpc são os coeficientes de acoplamento entre estas.
Fonte: Modificada de Cheon et al. (2011)
Inicialmente é feita uma descrição de um circuito contendo apenas as bobinas de
potência e transmissora, tal como em um transformador.
2.1.2 BOBINA DE POTÊNCIA E TRANSMISSORA (TRANSFORMADOR)
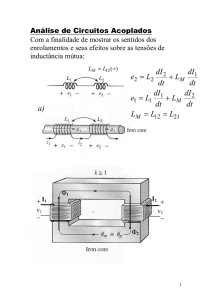
A Figura 4 mostra o esquema contendo apenas as bobinas de potência e
transmissora denominadas 1 e 2, o coeficiente de acoplamento associado, e o
circuito elétrico equivalente. Nesta situação o circuito pode ser analisado tal como
em um transformador. As equações de um transformador são bem descritas na
literatura. A mútua indutância é relacionada ao coeficiente de acoplamento e
indutâncias das bobinas. Cada bobina possui uma frequência de ressonância, neste
caso diferentes, dadas pela interação entre indutância e capacitância parasita. Um
conjunto de equações para descrever o circuito da Figura 2 é dado por,
𝑀12 = 𝑘12 √𝐿1 𝐿2
𝑖1 =
𝑉1
𝑍𝑜
+ 𝑗𝜔𝐶1 𝑉1 + 𝑖𝐿1
𝑉1 = 𝑗𝜔𝐿1 𝑖𝐿1 + 𝑗𝜔𝑀12 𝑖𝐿2
0=
𝑉2
𝑍𝑜
+ 𝑗𝜔𝐶2 𝑉2 + 𝑖𝐿2
(10)
(11)
(12)
(13)
17
Figura 4 – Modelo de transformador para a bobina de potência (1) e transmissora (2). a) Circuito
elétrico equivalente. b) Circuito equivalente com impedância mútua Z1M.
Fonte: Modificada de Cheon et al. (2011)
18
𝑉2 = 𝑗𝜔𝐿2 𝑖𝐿2 + 𝑗𝜔𝑀12 𝑖𝐿1
(14)
𝑘12 é o coeficiente de acoplamento, 𝑀12 a indutância mútua e 𝑍𝑜 a impedância
característica, geralmente 50 Ω.
A impedância de entrada à partir do gerador pode ser calculada das
expressões anteriores,
1
=
𝑍𝑖𝑛
𝑖1
𝑉1
−
1
𝑍𝑜
= 𝑗𝜔𝐶1 +
1
𝜔2 𝑀12 2
1
+𝑗𝜔𝐿2
1
+𝑗𝜔𝐶2
𝑍𝑜
(15)
+ 𝑗𝜔𝐿1
De acordo com (15) o circuito da Figura 4a) pode ser escrito como o da Figura 4b),
onde Z1M representa a impedância mútua, e é expressa por,
𝑍1𝑀 =
𝜔2 𝑀12 2
1
+𝑗𝜔𝐿2
1
+𝑗𝜔𝐶2
𝑍𝑜
𝜔2 𝑀12 2
=
𝑍2
=
𝜔2 𝑘12 2 𝐿1 𝐿2
𝑍2
(16)
Sendo 𝑍2 a impedância do circuito 2.
As características em frequência não são importantes em um transformador já
que a frequência de operação é muito mais baixa do quê a frequência de
ressonância. Entretanto um esquema de transferência de energia usando enlaces
ressonantes magneticamente acoplados opera na frequência de ressonância.
Considerando duas bobinas iguais, as frequências de ressonância são as mesmas,
isto é,
𝜔0 𝐿1 𝐶1 = 𝜔0 𝐿2 𝐶2 = 𝜔0 𝐿1 𝐶2
(17)
A impedância de entrada na frequência de ressonância é
1
𝑍𝑖𝑛 = 𝑗𝜔
0 𝐶1
1
//(𝑗𝜔0 𝐿1 + 𝑍1𝑀 )=𝑗𝜔
𝑍𝑖𝑛 =
0 𝐶1
//[𝑗𝜔0 𝐿1 (1 − 𝑘12 2 ) + 𝑘12 2 𝑍𝑜 ]
(18)
1
//[𝑗𝜔0 𝐿1 (1 − 𝑘12 2 ) + 𝑘12 2 𝑍𝑜 ]
𝑗𝜔0 𝐶1
Se a capacitância parasita é desprezível e 𝑘12 , é unitário, pode-se mostrar que 𝑍𝑖𝑛 =
𝑍𝑜 (condição de casamento perfeito) e a eficiência de acoplamento se torna 100%.
Entretanto, 𝑘12 cai drasticamente quando a distância entre as bobinas aumenta e 𝑍𝑖𝑛
se distancia de 𝑍𝑜 , a condição de casamento é perdida e a eficiência de
acoplamento diminui drasticamente. Esta é a principal razão pela qual a
transferência de energia em maiores distâncias é impossível em um transformador e
também em esquemas baseados em indução eletromagnética. Esta análise também
mostra a fragilidade do esquema para transmissão utilizando duas bobinas na
19
ressonância, já que este se mostra muito sensível ao descasamento de impedância
com o aumento da distância.
2.1.3 ESQUEMA COMPLETO (4 BOBINAS)
O esquema completo é mostrado na Figura 3. Considerando os interacoplamentos (Kpr, Ktc e Kpc) entre bobinas não adjacentes desprezíveis, tem-se o
circuito equivalente da Figura 5 e o seguinte conjunto de equações,
Figura 5 – Circuito elétrico equivalente ao da Figura 3. As indutâncias mútuas de uma bobina para a
outra são representadas por M com os respectivos sub-índices.
Fonte: Modificada de Cheon et.al (2011)
𝑉
𝑖𝑠 = 𝑍𝑠 + 𝑗𝜔𝐶𝑝 𝑉𝑠 + 𝑖1
(19)
𝑉𝑠 = 𝑗𝜔𝐿𝑝 𝑖1 + 𝑗𝜔𝑀𝑝𝑡 𝑖2
(20)
𝑜
𝑖
2
0 = 𝑗𝜔𝐿𝑡 𝑖2 + 𝑗𝜔𝑀𝑝𝑡 𝑖1 + 𝑗𝜔𝑀𝑡𝑟 𝑖3 + 𝑗𝜔𝐶
𝑡
𝑖
3
0 = 𝑗𝜔𝐿𝑟 𝑖3 + 𝑗𝜔𝑀𝑡𝑟 𝑖2 + 𝑗𝜔𝑀𝑟𝑐 𝑖4 + 𝑗𝜔𝐶
𝑟
𝑉
(21)
(22)
0 = 𝑍4 + 𝑗𝜔𝐶𝑐 𝑉4 + 𝑖4
(23)
𝑉4 = 𝑗𝜔𝐿𝑐 𝑖4 + 𝑗𝜔𝑀𝑟𝑐 𝑖3
(24)
𝑜
É assumido o caso sem perdas por simplicidade. A impedância de entrada a partir
do gerador pode ser obtida como no caso de duas bobinas da seção anterior. Porém
calcula-se a impedância mútua sucessivamente a partir da porta de saída, ou seja, a
impedância mútua da bobina de carga para a receptora, da receptora para a
transmissora e da transmissora para a de potência.
20
A impedância mútua 𝑍𝑅𝑀 refletida na bobina receptora pela bobina de carga
é,
𝑍𝑅𝑀 =
𝜔2 𝑀𝑅𝐶 2
1
+𝑗𝜔𝐿𝐶
1
+𝑗𝜔𝐶𝐶
𝑍𝑜
𝜔2 𝑘𝑅𝐶 2 𝐿𝑅 𝐿𝐶
=
(25)
𝑍𝐶
onde 𝑍𝐶 é a impedância do circuito de carga (circuito 4).
A impedância mútua 𝑍𝑇𝑀 refletida na bobina transmissora pela receptora (e
de carga) é,
𝑍𝑇𝑀 =
𝜔2 𝑀𝑇𝑅 2
𝑍𝑅𝑀 +
1
+𝑗𝜔𝐿𝑅
𝑗𝜔𝐶𝑅
=
𝜔2 𝑘𝑇𝑅 2 𝐿𝑇 𝐿𝑅
(26)
𝑍𝑅
onde 𝑍𝑅 é a impedância do circuito receptor (circuito 3).
A impedância mútua 𝑍𝑃𝑀 refletida na bobina de potência pela transmissora (e
receptora e de carga) é,
𝑍𝑃𝑀 =
𝜔2 𝑀𝑃𝑇 2
1
+𝑗𝜔𝐿𝑇
𝑗𝜔𝐶𝑇
𝑍𝑇𝑀 +
=
𝜔2 𝑘𝑃𝑇 2 𝐿𝑃 𝐿𝑇
(27)
𝑍𝑇
onde 𝑍𝑇 é a impedância do circuito transmissor (circuito 2). Substituindo (25) e (26)
em (27),
𝑍𝑃𝑀 =
𝜔2 𝑘𝑃𝑇 2 𝐿𝑃 𝐿𝑇
(28)
𝜔2 𝑘𝑇𝑅 2 𝐿𝑇 𝐿𝑅
1
+
+𝑗𝜔𝐿𝑇
2
2
𝑗𝜔𝐶
𝜔 𝑘𝑅𝐶 𝐿𝑅 𝐿𝐶
𝑇
1
+
+𝑗𝜔𝐿
𝑅
1
+𝑗𝜔𝐶𝐶 +𝑗𝜔𝐿𝐶 𝑗𝜔𝐶𝑅
𝑍𝑜
Como a frequência nas bobinas receptora e transmissora são iguais, temos que
1
1
𝜔0 2 𝐿𝑡 𝐶𝑡 = 𝜔0 2 𝐿𝑅 𝐶𝑅 = 1 e 𝑗𝜔𝐶 + 𝑗𝜔𝐿𝑇 =
𝑗𝜔𝐶𝑅
𝑡
+ 𝑗𝜔𝐿𝑅 = 0. Portanto (28) se reduz a,
2
𝑍𝑃𝑀 =
𝑘 𝑘
𝜔0 2 ( 𝑃𝑇 𝑅𝐶 ) 𝐿𝑃 𝐿𝐶
𝑘
1
𝑇𝑅
(29)
+𝑗 𝜔0 𝐿𝐶
1
+𝑗𝜔0 𝐶𝐶
𝑍𝑜
A equação (29) é muito parecida a expressão (16) para a impedância mútua para
um transformador de 2 bobinas. Na realidade, as duas expressões só divergem pelo
𝑘
𝑘
2
𝑅𝐶
termo da constante de acoplamento que para o circuito completo é ( 𝑃𝑇
) , desta
𝑘𝑇𝑅
maneira um circuito equivalente ao esquema com 4 bobinas é apresentado na
Figura 6.
21
Figura 6 – Circuito equivalente ao esquema com 4 bobinas.
Fonte: Modificada de Cheon et.al (2011)
Com base na Figura 6, nota-se portanto que o esquema com 4 bobinas pode ser
pensado como um acoplamento entre bobina de potência e de carga considerando
𝑘
𝑘
𝑅𝐶
apenas um coeficiente de acoplamento especial dado por 𝑃𝑇
.
𝑘𝑇𝑅
Para bobinas de potência e de carga iguais (𝐿𝑃= 𝐿𝐶 ) e com frequências de
ressonância iguais, pode-se escrever (29) como,
𝑍𝑃𝑀 = −𝑗𝜔0 𝐿𝑃 + 𝑍𝑜
Assumindo
𝑘𝑃𝑇 𝑘𝑅𝐶
𝑘𝑇𝑅
(30)
igual à unidade, então a impedância de entrada pode ser dada
por,
1
𝑍𝑖𝑛 = 𝑗𝜔
1
0 𝐶𝑃
//𝑗𝜔0 𝐿𝑃 + 𝑍𝑃𝑀 = 𝑗𝜔
𝑍𝑖𝑛 =
0 𝐶𝑃
//𝑍𝑜
(31)
1
// 𝑍𝑜
𝑗𝜔0 𝐶𝑃
Sendo 𝐶𝑃 desprezível 𝑍𝑖𝑛 = 𝑍𝑜 , temos o casamento perfeito e a eficiência de
acoplamento é máxima.
Apesar do coeficiente de acoplamento entre as bobinas receptora e
transmissora 𝑘 𝑇𝑅 ser pequeno devido à grande distância entre estas, pode-se tornar
𝑘𝑃𝑇 𝑘𝑅𝐶
𝑘𝑇𝑅
unitário ao ajustar 𝑘𝑃𝑇 e 𝑘𝑅𝐶 . Isto na prática é realizado ao se ajustar a
distância entre a bobina de potência e transmissora, e entre a bobina receptora e de
carga. Desta maneira é possível alcançar alta eficiência de acoplamento a médias
distâncias.
22
2.2 ENLACES RESSONANTES COM ELEMENTOS CONCENTRADOS (LC)
Apesar de enlaces autorressonantes possuírem algumas vantagens por não
necessitarem de um capacitor, muitos sistemas práticos de transmissão de energia
sem fio utilizam capacitores em série com a bobina obtendo-se uma ressonância LC
série com valor mais baixo de frequência. Uma frequência de valor mais baixo
simplifica o projeto dos equipamentos envolvidos no sistema de transmissão de
energia, principalmente em sistemas de maior potência. Por exemplo, este tipo de
sistema tem sido utilizado para carregamento da bateria de veículos elétricos (LI; MI,
2014).
A seguir será mostrada uma análise do sistema com 2 e 4 bobinas utilizando
ressonância LC série tendo como enfoque a eficiência e a máxima transferência de
potência, baseado no trabalho de Abatti, Pichorim e Miranda (2014).
2.2.1 SISTEMAS COM 2 BOBINAS
A Figura 7 mostra o circuito equivalente de um sistema com 2 bobinas.
R1
C1
M12
C2
i2
i1
v
R2
L1
L2
Figura 7. Representação de um sistema de 2 bobinas
Fonte: Abatti, Pichorim e Miranda (2014)
Considerando ambos circuitos sintonizados na mesma frequência de
ressonância angular (𝜔0 −1 = √𝐿1 𝐶1 = √𝐿2 𝐶2 ), pode ser escrito
𝑣 = 𝑅1 𝑖1 ± 𝑗𝜔0 𝑀12 𝑖2 ,
e
(32)
23
0 = ±𝑗𝜔0 𝑀12 𝑖1 + 𝑅2 𝑖2 ,
(33)
aonde, M12 é a mútua indutância, R1 é a resistência total do circuito transmissor
(incluindo as resistências internas da fonte e dos elementos indutor (L1) e capacitor
(C1)), e R2 a resistência total do circuito receptor (a soma das resistências internas da
resistência do capacitor (C2) e do indutor (L2) com a resistência de carga (RL)).
A potência elétrica é calculada multiplicando a resistência pelo modulo da
corrente ao quadrado tal que usando (32) e (33) pode ser escrito
𝑃1 =
𝑅1 𝑅2 2 𝑣 2
2
(𝑅1 𝑅2 +𝜔0 2 𝑀12 2 )
,
(34)
e
𝑃2 =
𝑅2 𝜔0 2 𝑀12 2 𝑣 2
(𝑅1 𝑅2 +𝜔0 2 𝑀12 2 )
2
,
(35)
Aonde, P1 e P2 são as potências elétricas dissipadas em R1 e R2, respectivamente.
Derivando (35) em relação a M12 e igualando o resultado a zero, após alguma
manipulação algébrica, chega-se em
𝜔0 2 𝑀12 2 = 𝑅1 𝑅2 .
(36)
Esta é a condição de máxima transferência de potência (MTP) para um
sistema de 2 bobinas (que (36) é uma condição de máximo pode ser demonstrado
tomando a segunda derivada de (36) com relação a M12 e igualando a zero). Além
disso, usando (36) em (34) e (35) leva à
𝑣2
𝑃1 = 𝑃2𝑀𝐴𝑋 = 4.𝑅 ,
1
(37)
tal como o clássico teorema da máxima transferência de potência ensina.
Para propósitos de comparação é interessante calcular a potência relativa
transferida para R2 dividindo (35) por (37), resultando em
24
𝑃2
=
𝑃2𝑀𝐴𝑋
4𝑅1 𝑅2 𝜔0 2 𝑀12 2
(𝑅1 𝑅2 +𝜔0 2 𝑀12 2 )
2
.
(38)
Dividindo a potência transferida para R2 (P2) pela potência total (P1+P2), a
eficiência da transferência (𝜂) pode ser calculada,
𝜔0 2 𝑀12 2
𝜂=𝑅
1 𝑅2 +𝜔0
2𝑀 2
12
.
(39)
Note que, também como o teorema da MTP ensina, usando (36) em (39) resulta em
𝜂 =1/2.
2.2.2 SISTEMAS COM 4 BOBINAS
A Figura 8 mostra o circuito equivalente do sistema com 4 bobinas.
M24
R1
C1
M12
C2
C3
i2
i1
v
M23
L1
M34
C4
i3
L2
L3
R2
i4
R3
R4
L4
M13
M14
Figura 8. Representação de um sistema com 4 bobinas.
Fonte: Abatti, Pichorim e Miranda (2014)
Considerando todos os circuitos sintonizados na mesma frequência de
ressonância angular (𝜔0 −1 = √𝐿1 𝐶1 = √𝐿2 𝐶2 = √𝐿3 𝐶3 = √𝐿4 𝐶4 ), e negligenciando a
influência das mútuas indutâncias M13, M14, e M24, pode ser escrito
𝑣 = (𝑅1 𝑖1 ) ± (𝑗𝜔0 𝑀12 𝑖2 ) ,
(40)
25
0 = (±𝑗𝜔0 𝑀12 𝑖1 ) + (𝑅2 𝑖2 ) ± (𝑗𝜔0 𝑀23 𝑖3 ) ,
(41)
0 = (±𝑗𝜔0 𝑀23 𝑖2 ) + (𝑅3 𝑖3 ) ± (𝑗𝜔0 𝑀34 𝑖4 ) ,
(42)
e
0 = (±𝑗𝜔0 𝑀34 𝑖3 ) + (𝑅4 𝑖4 ) ,
(43)
aonde M12, M23 e M34 são as mútua indutâncias, e R1, R2, R3 e R4 as resistências
individuais dos circuitos. Note que R4 é a soma das resistências internas da
capacitância (C4) e da indutância (L4) com a resistência de carga (RL).
Manipulando (40), (41), (42), e (43), as correntes i1, i2, i3, e i4 podem ser
calculadas tal que a potência dissipada em R1, R2, R3, e R4 podem ser escritas como
𝑣2
𝑃1 = 𝐶 2 𝑅1 ,
𝑃2 =
𝑃3 =
𝜔0 2 𝑀12 2 𝑣 2
𝐵2 𝐶 2
(44)
𝑅2 ,
𝜔0 2 𝑀12 2 𝜔0 2 𝑀23 2 𝑣 2
𝐴2 𝐵2 𝐶 2
(45)
𝑅3 ,
(46)
e
𝑃4 =
𝜔0 2 𝑀12 2 𝜔0 2 𝑀23 2 𝜔0 2 𝑀34 2 𝑣 2
𝐴2 𝐵2 𝐶 2 𝑅4
,
(47)
respectivamente, onde A, B, e C são dadas por
𝐴 = 𝑅3 +
𝐵 = 𝑅2 +
𝜔0 2 𝑀34 2
𝑅4
𝜔0 2 𝑀23 2
𝐴
,
,
e,
𝐶 = 𝑅1 +
𝜔0 2 𝑀12 2
𝐵
,
respectivamente. Logicamente, usando o sistema de 2 bobinas como guia, as
potências P2 e P3 devem ser o menor possível, tal que, idealmente, R2=R3=0.
26
Usando a condição anterior (R2=R3=0) em (44), (45), (46), e (47), e relembrando que a
mútua indutância (na forma geral Mxy) é definida como 𝑀𝑥𝑦 = 𝑘𝑥𝑦 √𝐿𝑥 𝐿𝑦 , aonde kxy é
o coeficiente de acoplamento, variando entre zero e um, pode ser escrito
2
𝑃1 =
𝑅1 𝑅4 2 (𝑘23 2 ) 𝑣 2
2
(𝑅1 𝑅4 𝑘23 2 +𝑘12 2 𝑘34 2 𝜔0 𝐿1 𝐿4 )
2
,
(48)
e
𝑃4 =
𝑘12 2 𝑘23 2 𝑘34 2 𝜔0 2 𝐿1 𝐿4 𝑅4 𝑣2
2
2
(𝑅1 𝑅4 𝑘23 2 +𝑘12 2 𝑘34 2 𝜔0 𝐿1 𝐿4 )
,
(49)
com, evidentemente, P2=P3=0.
Tomando a derivada de (49), também usando o sistema de 2 bobinas como
guia, em relação a k23 e igualando o resultado a zero tem-se
𝑘23 2 𝑅1 𝑅4 = 𝑘12 2 𝑘34 2 𝜔0 2 𝐿1 𝐿4 .
(50)
Esta é a condição de máxima transferência de potência (MTP) para um
sistema com 4 bobinas sem perdas de potência nos circuitos de comunicação. Note
que usando (50) em (48) e (49) leva a
𝑣2
𝑃1 = 𝑃4𝑀𝐴𝑋 = 4𝑅 ,
(51)
1
conforme o teorema da MTP ensina.
Para propósitos de comparação é também interessante computar a potência
relativa transferida para R4, dividindo (49) por (51) resultando,
2
𝑃4
𝑃4𝑀𝐴𝑋
=
4𝑅1 𝑅4 𝑘12 2 𝑘23 2 𝑘34 2 𝜔0 𝐿1 𝐿4
2
(𝑅1 𝑅4 𝑘23 2 +𝑘12 2 𝑘34 2 𝜔0 𝐿1 𝐿4 )
2
,
(52)
A eficiência do sistema (𝜂), também com R2=R3=0, pode ser definida como
𝜂=𝑃
𝑃4
1 +𝑃2 +𝑃3 +𝑃4
=
𝑘12 2 𝑘34 2 𝜔0 2 𝐿1 𝐿4
2
𝑅1 𝑅4 𝑘23 2 +𝑘12 2 𝑘34 2 𝜔0 𝐿1 𝐿4
,
(53)
Note que, seguindo o clássico teorema da MTP, usando (50) em (53) resulta em
𝜂 = 1/2.
27
Entretanto, na prática R2 e R3 não são geralmente desprezíveis. Neste caso, a
potência relativa transferida para R4 é dada por
𝑃4
𝑃4𝑀𝐴𝑋
=
4𝑅1 𝑅4 𝜔0 2 𝑀12 2 𝜔0 2 𝑀23 2 𝜔0 2 𝑀34 2
(𝑅1 𝑅4 𝜔0 2 𝑀23 2 +(𝑅1 𝑅2 +𝜔0 2 𝑀12 2 )(𝑅3 𝑅4 +𝜔0 2 𝑀34 2 ))
(54)
2
enquanto η é dado por
𝜂 = (𝑅
𝜔0 2 𝑀12 2 𝜔0 2 𝑀23 2 𝜔0 2 𝑀34 2 𝑅4
4 𝜔0
2 𝑀 2 +𝑅 (𝑅 𝑅 +𝜔 2 𝑀 2 ))(𝑅 𝑅 𝜔 2 𝑀 2 +(𝑅 𝑅 +𝜔 2 𝑀 2 )(𝑅 𝑅 +𝜔 2 𝑀 2 ))
23
2 3 4
0
34
1 4 0
23
1 2
0
12
3 4
0
34
(55)
Observe que, no caso de R2=R3=0, (54) e (55) se tornam (52) e (53),
respectivamente. Além disso, pode ser visto que (54) e (55), devido ao seu formato,
apresentam um ponto de máximo. Portanto, tomando a derivada de ambos em
relação a k23 e igualando o resultado a zero tem-se,
𝑅1 𝑅4 𝜔0 2 𝑀23 2 = (𝑅1 𝑅2 + 𝜔0 2 𝑀12 2 )(𝑅3 𝑅4 + 𝜔0 2 𝑀34 2 )
,
(56)
,
(57)
e
[𝑅1 𝑅4 2 (𝜔0 2 𝑀23 2 )2 = (𝑅1 𝑅2 + 𝜔0 2 𝑀12 2 )(𝑅3 𝑅4 + 𝜔0 2 𝑀34 2 )2 𝑅2
respectivamente.
Observe que (56) e (57) mostram que o ponto de máximo de (54) e (55) não
são coincidentes. Além disso, note que no caso de R2=R3=0 (56) se torna (50), e (57)
não possui mais significado, isto é, η não possui um ponto de máximo (em termos de
derivada igual a zero).
Finalmente, substituindo (56) em (54) e (57) em (55) pode ser visto que o ponto de
máximo em (54) e (55) são sempre, como esperado, menores do que a unidade.
No presente trabalho os testes práticos serão desenvolvidos com base na
teoria apresentada na seção 2.2, ou seja, enlaces ressonantes utilizando elementos
concentrados (LC), onde serão abordadas principalmente a eficiência e a
transferência relativa de potência, tal como apresentado. A escolha desta técnica se
deveu a experiência prévia dos autores e também a motivação de que, a primeiro
momento, esta técnica possui maior aplicação prática (LI; MI, 2014).
28
2.3 TRABALHOS RECENTES
A seguir são mostrados alguns trabalhos atuais e que fazem uso da técnica
aqui estudada.
Zhou e Yang (2012) apresentam um método para calcular a frequência de
ressonância de bobinas planares utilizadas para fins de transmissão de energia. O
método se baseia em um circuito elétrico equivalente e na análise tridimensional
pelo método dos elementos finitos.
Huang, Chen e Liu (2009) apresentam um enlace ressonante com ajuste
automático da frequência de ressonância. Os autores mostram uma melhora de até
33 % na eficiência ao utilizar este esquema.
Breitkreutz e Henke (2013) apresentam um método baseado na teoria de
linhas de transmissão para calcular a autorressonância de bobinas espirais
utilizadas em transmissão de energia.
Artan et al. (2011) apresentam um trabalho provando a vantagem de se
utilizar bobinas multicamadas para transferência de potência para sensores
implantados em tecidos biológicos.
Zhang et al. (2009) mostram a vantagem de se utilizar a transferência de
energia por enlaces ressonantes magneticamente acoplados para alimentar
sensores e outros dispositivos biomédicos.
Li et al. (2013) utilizam bobinas planares flexíveis de alto fator de qualidade
para o esquema de transferência de energia mostrando a vantagem de se utilizar
este tipo de bobina.
Zhao et al. (2012) fazem um estudo comparativo entre a técnica apresentada
neste trabalho e a técnica da indução eletromagnética para fins de transferência de
energia. Os autores mostram a vantagem de se utilizar o esquema com duas
bobinas trabalhando na ressonância.
Gozalvez (2007) apresenta um trabalho de revisão onde também aponta
tendências futuras, aplicações industriais bem como energias renováveis utilizando a
técnica estudada.
29
2.4 NORMA PARA EXPOSIÇÃO A CAMPOS
Neste item será apresentado um resumo da norma ABNT 03:077.01 Limites
para a Exposição a Campos Elétricos, Magnéticos e Eletromagnéticos variáveis no
Tempo (até 300 GHz), esta norma foi baseada na Guidelines for Limiting Exposure
to Time Varying Electric, Magnetic, and Electromagnetic fields (up to 300 GHz)”,
publicado em Health Physics, vol.74, n.4, pp.494-522, April 1998.
2.4.1 EFEITO CAUSADO PELO CAMPO ELÉTRICO OU MAGNÉTICO
2.4.1.1
MECANISMOS
DE
ACOPLAMENTO
ENTRE
CAMPOS
ELETROMAGNÉTICOS E O CORPO HUMANO
Há três mecanismos básicos de acoplamento, bem estabelecidos, através
dos quais campos elétricos e magnéticos variáveis no tempo interagem diretamente
com matéria viva:

Acoplamento a campos elétricos de baixa frequência;

Acoplamento a campos magnéticos de baixa frequência;

Absorção de energia de campos eletromagnéticos
2.4.1.2 ACOPLAMENTO A CAMPOS ELÉTRICOS DE BAIXA FREQUÊNCIA
A interação de campos elétricos variáveis no tempo, com o corpo humano,
resulta num fluxo de cargas elétricas (corrente elétrica), na polarização de cargas
ligadas (formação de dipolos elétricos), e na reorientação dos dipolos elétricos já
presentes no tecido.
2.4.1.3 ACOPLAMENTO A CAMPOS MAGNÉTICOS DE BAIXA
FREQUÊNCIA
A interação física de campos magnéticos variáveis no tempo, com o corpo
humano, resulta na indução de campos elétricos induzidos e correntes elétricas
circulantes. As amplitudes dos campos induzidos e a densidade da corrente são
proporcionais ao laço (caminho fechado) escolhido, à condutividade elétrica do
tecido, à taxa de variação e à amplitude da densidade do fluxo magnético. Para uma
30
dada amplitude e frequência do campo magnético, os campos elétricos mais
intensos são induzidos onde as dimensões do laço são maiores; sendo que o
caminho exato e a amplitude da corrente induzida em qualquer parte do corpo,
dependerão da condutividade elétrica do tecido. O corpo não é eletricamente
homogêneo; entretanto as densidades de correntes induzidas podem ser calculadas,
usando modelos que representam de maneira realística as propriedades anatômicas
e elétricas do corpo e recorrendo a métodos computacionais que têm grau elevado
de resolução anatômica.
2.4.1.4 ABSORÇÃO DA ENERGIA DE CAMPOS ELETROMAGNÉTICOS
A exposição a campos elétricos e magnéticos de frequência baixa resulta
normalmente em uma absorção de energia desprezível, sem elevação mensurável
da temperatura do corpo. Entretanto, a exposição a campos eletromagnéticos de
frequências acima de aproximadamente 100 kHz, pode conduzir a uma absorção
significativa de energia e a um aumento de temperatura. Em geral, a exposição a um
campo eletromagnético uniforme (onda plana) resulta em uma deposição e
distribuição de energia altamente não uniforme dentro do corpo, que precisa ser
avaliada por medidas dosimétricas e por cálculos. Com respeito à absorção da
energia pelo corpo humano, os campos eletromagnéticos podem ser divididos em
quatro faixas:

Frequências de aproximadamente 100 kHz a 20 MHz;

Frequência decrescente e pode ocorrer uma absorção significativa no
pescoço e nas pernas;

Frequências de aproximadamente 20 MHz a 300 MHz, nas quais pode
ocorrer uma absorção relativamente alta no corpo todo, e até mesmo
valores mais altos, se forem consideradas ressonâncias em partes do
corpo (p. ex.: na cabeça);

Frequências de aproximadamente 300 MHz à vários GHz, nas quais
ocorre absorção local significativa e não uniforme;

Frequências acima de 10 GHz, nas quais a absorção de energia ocorre
principalmente na superfície do corpo.
31
2.4.2 LIMITES PARA EXPOSIÇÃO OCUPACIONAL E DO PÚBLICO EM
GERAL
A população ocupacionalmente exposta compreende adultos que estão
geralmente expostos a condições conhecidas estão treinados para estar atentos ao
risco potencial e tomar as precauções apropriadas. Em contraste, o público em geral
consiste de pessoas de todas as idades e estados de saúde e pode incluir grupos ou
indivíduos particularmente suscetíveis.
Foram usadas bases científicas diferentes no desenvolvimento de restrições
básicas para as exposições em várias faixas de frequências:

Entre 1 Hz e 10 MHz, foram estabelecidas restrições básicas na
densidade de corrente para evitar efeitos em funções do sistema
nervoso;

Entre 100 kHz e 10 GHz, foram estabelecidas restrições básicas na
SAR , para evitar o estresse causado por aquecimento do corpo inteiro
e o aquecimento excessivo localizado em tecidos; sendo que na faixa
de 100 kHz a 10 MHz as restrições abrangem tanto a densidade de
corrente, como a SAR;

Entre 10 GHz e 300 GHz, foram estabelecidas restrições básicas na
densidade de potência, para evitar aquecimento excessivo em tecidos
superficiais ou próximos à superfície do corpo.
Na faixa de frequências de poucos Hz a 1 kHz, e em níveis de intensidade de
corrente induzida superiores a 100 mA.m2, são excedidos os limiares para
mudanças agudas na excitabilidade do sistema nervoso central e para outros efeitos
agudos, como a reversão do potencial evocado visualmente.
Tendo em vista as considerações de segurança feitas acima, foi decidido
que, para frequências na faixa de 4 Hz a 1 kHz, a exposição ocupacional deve ser
limitada a campos que induzem densidades de corrente menores que 10 mA.m-2; ou
seja, decidiu-se usar um fator de segurança igual a 10. Para o público em geral, foi
32
adotado um fator adicional de 5, resultando uma restrição básica para a exposição,
de 2 mA.m-2.
Abaixo de 4 Hz e acima de.1 kHz, as restrições básicas para densidade de
corrente induzida aumentam progressivamente, correspondendo ao aumento do
limiar para a estimulação de nervos nessas faixas de frequências.
Efeitos biológicos e na saúde, estabelecidos na faixa de frequências de 10
MHz até alguns GHz, são consistentes com respostas a uma elevação da
temperatura corporal superior a 1 ºC.
Em condições ambientais moderadas, este nível de aumento de temperatura
resulta da exposição de pessoas a uma SAR (taxa de absorção de corpo inteiro) de
corpo inteiro de aproximadamente 4 W.kg-1 durante cerca de 30 min.
Por essa razão, uma SAR média, de corpo inteiro, de 0,4 W.kg-1, foi
escolhida como sendo a restrição que garante proteção adequada no caso de
exposição ocupacional.
Um fator de segurança adicional, igual a 5, foi introduzido para a exposição
do público em geral, resultando, assim, um limite de 0,08 W.kg-1 para a SAR média
de corpo inteiro.
As restrições básicas inferiores para a exposição do público em geral, levam
em conta o fato de que a idade e o estado de saúde podem diferir do caso de
trabalhadores.
As tabelas 1 e 2 mostram um resumo dos limites para campos estabelecidos
pela norma.
Tabela 1 – Limites para SAR
33
Tabela 2 – Limites para campos
2.4.3 NÍVEIS DE REFERÊNCIA
Onde apropriado, os níveis de referência são obtidos das restrições básicas
por modelamento matemático e por extrapolação de resultados de investigações de
laboratório em frequências específicas. Os níveis são dados para a condição de
acoplamento máximo do campo com o indivíduo exposto, fornecendo. Os níveis são
ilustrados nas Figuras 9 e 10.
34
Figura 9 – Níveis de referência para exposição a campos elétricos variáveis no tempo.
Fonte: ABNT
35
Figura 10 – Níveis de referência para exposição a campos magnéticos variáveis no tempo.
Fonte: ABNT
36
3 RESULTADOS
Foram construídas 4 bobinas com 30 cm de diâmetro, fio de cobre esmaltado
com 0,91 mm de diâmetro e 56 espiras, onde no processo de confecção das
bobinas, especial cuidado foi tomado para se obter o máximo de precisão no
enrolamento, de maneira a se obter bobinas com indutâncias o mais próximas
possível. Os parâmetros elétricos das bobinas foram medidos com auxílio de um
analisador vetorial de impedâncias Agilent 4294A na faixa de 1 a 100 kHz. A
indutância série medida foi de 1,5 mH (variação menor que 0,1 mH entre as bobinas)
e a resistência série (RS) possui um valor de 5,6 Ω (perdas ôhmicas no fio).
Para se obter a ressonância foi utilizado um capacitor de poliéster de 3,3 nF e
com tensão máxima de 1600 V (este capacitor foi selecionado visando os testes com
maiores potências que serão apresentados na próxima seção). Um ponto crítico do
projeto é obter as mesmas frequências de ressonância para todos os circuitos
utilizados. Considerando a variação de 10 % em torno do valor nominal dos
capacitores, a capacitância exata na faixa de 40 a 75 kHz (próxima a frequência de
operação) foi medida em um lote de aproximadamente 30 capacitores com o auxílio
do analisador de impedância. Com estes valores, e com os valores de indutância
medidos, alcançou-se valores de frequência de 71,32 kHz com precisão de 0,1 kHz
em todos os circuitos. A resistência equivalente do capacitor foi desprezada, uma
vez que o valor medido no analisador foi da ordem de mΩ.
Uma vez que a análise apresentada na seção 2.2 é fortemente dependente
do coeficiente de acoplamento (k), primeiramente foi levantada a curva de k em
função da distância entre duas bobinas coaxialmente dispostas considerando a
teoria apresentada em (ABATTI; PICHORIM; SCHNEIDER, 2008) e utilizando o
software excel. Para a simulação as dimensões e a indutância medida foram
utilizadas. Adicionalmente, um ensaio para medir k prático também foi realizado. Foi
utilizado um gerador de funções Tektronix CFG253 para excitar uma bobina
(primário) em uma baixa frequência de 10 kHz para evitar a influência de
capacitâncias parasitas (logicamente neste teste não se usa o capacitor em série).
Um oscilador Agilent MSO6034 é utilizado para se medir a tensão sobre os terminais
do circuito primário (v1) e sobre os terminais abertos da segunda bobina (v2)
(secundário), enquanto a distância entre as bobinas é variada. Uma vez que a
corrente no secundário é zero (terminais abertos), v1 = 𝐿1 . 𝑑𝑖1 ⁄𝑑𝑡 e v2 = 𝑀12 . 𝑑𝑖1 ⁄𝑑𝑡.
37
Como as indutâncias de ambas as bobinas são iguais (L1=L2=L), então 𝑘 = 𝑀12 /𝐿, e
após pouca manipulação 𝑘 = 𝑣2 ⁄𝑣1 . A Figura 11 mostra o coeficiente de
acoplamento medido e simulado em função da distância.
0,5
0,45
0,4
0,35
k
0,3
0,25
0,2
0,15
0,1
0,05
0
0
10
20
30
40
50
60
70
80
90
100
d (cm)
Figura 11. Coeficiente de acoplamento medido (pontos) e simulado através de (ABATTI;
PICHORIM; SCHNEIDER, 2008) (linha sólida).
Para medir a eficiência e a transferência relativa de potência, é necessário
conhecer as correntes no circuito 1 e na carga, para isso foi utilizado um resistor (R0)
de 3,9 Ω em série com L1 e C1 o que possibilita medir a corrente circulante no
circuito 1. Para a resistência de carga (Rl) foi utilizado um resistor de 268 Ω, sendo a
corrente no circuito 4 medida através da queda de tensão no mesmo. As indutâncias
dos resistores utilizados foram desprezadas uma vez que os valores medidos são da
ordem de nH. Um sinal de 72 kHz e 7,7 Vrms foi aplicado sobre o circuito 1. Para
confirmar que a frequência de ressonância não foi alterada por outros parâmetros do
circuito tais como capacitâncias parasitas de cabos de medição, esta foi sintonizada
em função do ponto de mínima tensão medido sobre o circuito (ressonância série)
quando livre de influências das outras bobinas (bobina isolada no espaço). Outro
parâmetro que deve ser levado em consideração é a impedância de saída do
gerador (RG) sendo que esta vai compor R1 (Figuras 7 e 8), o valor exato para o
gerador utilizado é de 48 Ω. Como todos os parâmetros levados em consideração é
possível calcular R1 = R0 + RS + RG = 57,02 Ω. A resistência de carga total RL será
38
composta pela resistência nominal da carga e as perdas no fio da bobina.
Finalmente, a potência dissipada em R1 é 𝑃1 = 𝑅1 ⋅ 𝑖1 2 e na carga RL é 𝑃𝐿 = 𝑅𝐿 ⋅ 𝑖𝑙 2 . A
Figura 12 mostra o setup utilizado nos testes.
Figura12. Setup utilizado nos testes mostrando o osciloscópio, o gerador de funções e as bobinas
construídos.
3.1 SISTEMA COM 2 BOBINAS
Para o sistema com 2 bobinas, a eficiência medida é dada por P1/(P1+PL) e a
transferência relativa de potência é dada por PL/P2MAX. A distância entre as bobinas
foi variada de 5,5 a 91,5 cm em passos de 2 cm e os valores de tensão são medidos
a cada passo. Os valores teóricos são calculados de (38) e (39). A Figura 13 mostra
os valores medidos e calculados para a eficiência e transferência relativa de
potência. A máxima transferência de potência ocorre para a distância de 7,5 cm e
neste caso a eficiência é de aproximadamente 50% conforme apresentado na teoria.
39
1,2
Rel.Pow.Trf
Eff
Eff. & Transf. Rel.
1
Rel.Pow.Calc
Eff.Calc
0,8
0,6
0,4
0,2
0
0
10
20
30
40
50
60
70
80
90
100
d(cm)
Figura 13. Comparação entre eficiência e transferência relativa de potência medidas (pontos) e
calculadas (linhas cheias) através de (38) e (39).
É interessante também notar o efeito de diferentes valores de carga nas curvas de
transferência relativa de potência e eficiência. Nas Figuras 14 e 15 são mostradas
simulações para os valores de 68, 168 e 268 Ω.
40
1,00E+00
9,00E-01
268ohms
8,00E-01
168ohms
7,00E-01
68ohms
Transf. Rel.
6,00E-01
5,00E-01
4,00E-01
3,00E-01
2,00E-01
1,00E-01
0,00E+00
0
10
20
30
40
50
60
d(cm)
Figura 14. Efeito de diferentes cargas (68, 168 e 268 Ω) na curva de transferência relativa de
potência.
1,00E+00
9,00E-01
268ohms
8,00E-01
168ohms
7,00E-01
68ohms
Transf. Rel.
6,00E-01
5,00E-01
4,00E-01
3,00E-01
2,00E-01
1,00E-01
0,00E+00
0
10
20
30
40
d(cm)
Figura 15. Efeito de diferentes cargas (68, 168 e 268 Ω) na curva da eficiência.
50
60
41
3.2 SISTEMA COM 4 BOBINAS
No sistema de 4 bobinas a eficiência medida pode ser dada pela relação
PL/(P1+P2+P3+PL). Entretanto, as resistências R2 e R3 não são resistores reais mas
sim representam as perdas ôhmicas nos fios, logo P2 e P3 não podem ser medidas
diretamente. Sendo assim, e considerando que toda a potência dissipada é
dissipada nas perdas ôhmicas, a eficiência pode ser alternativamente calculada por
PL/PG, aonde PG = vG⋅i1. A distância entre as bobinas 1 e 2, e 3 e 4 são fixas em 20
cm, enquanto que a distância entre as bobinas 2 e 3 é variada. Desta maneira
evitam-se os inter-acoplamentos entre circuitos não adjacentes (1-3, 1-4 e 2-4). Os
valores teóricos são calculados através de (54) e (55). Os resultados são mostrados
na Figura 16. Neste caso, nota-se que conforme previsto na teoria, a eficiência
passa por um máximo.
0,6
Eff
RelPow
0,5
Eff & Transf. Rel. Pot.
EffCalc
0,4
RelPowCalc
0,3
0,2
0,1
0
0
10
20
30
40
50
60
70
80
90
d(cm)
Figura 16. Comparação entre eficiência e transferência relativa de potência medidas (pontos) e
calculadas (linhas cheias) através de (54) e (55).
Um segundo experimento foi realizado mantendo-se a distância entre as bobinas 1 e
2 fixas em 32 cm e as bobinas 3 e 4 fixas em 20 cm. Os resultados são mostrados
na Figura 17.
42
0,4
Eff
0,35
RelPow
Eff. & Transf. Rel. Pot
0,3
EffCalc
RelPowCalc
0,25
0,2
0,15
0,1
0,05
0
0
10
20
30
40
50
60
70
80
90
d(cm)
Figura 17. Comparação entre eficiência e transferência relativa de potência medidas (pontos) e
calculadas (linhas cheias) através de (54) e (55).
As Figuras 18 e 19 mostram o efeito de diferentes valores de carga nas curvas de
transferência relativa de potência e eficiência, no caso de espaçamento de 20 cm
entre circuitos 1-2 e 3-4.
0,8
268ohms
168 ohms
0,7
68ohms
Transf. Rel. Pot.
0,6
0,5
0,4
0,3
0,2
0,1
0
0
10
20
30
40
50
60
70
80
90
d(cm)
Figura 18. Efeito de diferentes cargas (68, 168 e 268 Ω) na curva de transferência relativa de potência
no sistema de 4 bobinas.
43
268ohms
0,45
168 ohms
0,4
68ohms
0,35
Eficiência
0,3
0,25
0,2
0,15
0,1
0,05
0
0
10
20
30
40
50
60
70
80
90
d(cm)
Figura 19. Efeito de diferentes cargas (68, 168 e 268 Ω) na curva de eficiência para o sistema de 4
bobinas.
Em seguida são apresentados testes com maiores potências utilizando uma
lâmpada de 25 W como carga.
3.3 TESTES COM ALTA POTÊNCIA
Para os testes com alta potência o sistema sofreu algumas modificações. Um
amplificador de RF E&I 1040l que fornece uma potência máxima de 400 W na faixa
de 30 kHz a 5 MHz foi utilizado para amplificar o sinal proveniente do gerador de
funções. A impedância de entrada e saída do amplificador é de 50 Ω e, portanto,
está casado com a impedância de saída do gerador. Como carga foi utilizada uma
lâmpada incandescente de 25 W para 127 Vrms.
Um detalhe importante durante a execução dos experimentos e testes é de
que diversos capacitores foram “queimados” ou danificados apesar de suportarem
uma tensão de 1600 V! Isso se deve ao fato de que na ressonância série apesar de
a tensão total ser teoricamente zero (lembrando que que as reatâncias Xl e Xc se
anulam), a tensão individual em cima da bobina e do capacitor é Q vezes maior do
que a tensão de operação, sendo Q o fator de qualidade (MARCUS; MARCUS,
44
1964). Após vários testes, para resolver este problema, foram utilizados dois
capacitores em paralelo de maneira a dividir a corrente que passa sobre cada
capacitor e, portanto, a tensão em cada um, e dessa maneira foi possível estabilizar
o sistema e realizar os testes. Para este caso a nova frequência de ressonância
possui o valor de 50,4 kHz. A Figura 20 mostra o sistema completo utilizado nos
testes.
Figura 20. Sistema completo utilizado nos testes de potência.
Para os testes a metodologia utilizada foi monitorar a tensão sobre a carga
(lâmpada de 25 W), uma vez que a tensão de aproximadamente 127 Vrms é atingida
considera-se que a lâmpada possui brilho máximo e, portanto, dissipa a potência de
25 W. Após alguns testes iniciais, definiu-se que a tensão sobre o circuito 1
conectado ao amplificador não seria monitorada, uma vez que devido a alta potência
de saída o osciloscópio correria riscos de ser danificado.
45
3.3.1 SISTEMA COM 2 BOBINAS
Primeiramente os circuitos 1 e 2 foram mantidos a distância de 8 cm. Com o sistema
em operação, a tensão de saída do gerador de funções é cuidadosamente alterada
até o ponto em que se atingiu 127 Vrms medido nos terminais da lâmpada
conectada ao circuito 2. De posse da tensão medida, da resistência da lâmpada
para a tensão de 127 Vrms e 25 W, acha-se a corrente i2. Utilizando a equação (33)
acha-se i1, e através de (32) calcula-se v1. De posse destes valores pode-se calcular
as potências P1 e P2 e a respectiva eficiência (para estes testes utilizou-se apenas
os valores de eficiência). Para este caso a eficiência medida é de 24,28 %. A
eficiência calculada é dada por (39), sendo que para a distância de 8 cm esta possui
um valor de 24,5 % conforme mostra a Figura 21.
1,00E+00
Rel.Pow.Calc
9,00E-01
8,00E-01
Eff.Calc
Transf Rel. e Eff
7,00E-01
6,00E-01
5,00E-01
4,00E-01
3,00E-01
2,00E-01
1,00E-01
0,00E+00
0
5
10
15
20
25
30
d(cm)
Figura 21. Eficiência e transferência relativa de potência simuladas, para o sistema de 2 bobinas e
lâmpada de 25 W e 127 Vrms como carga.
Em seguida as bobinas foram posicionadas a distância de 15 cm e os mesmos
passos anteriores foram realizados. Neste caso temos uma eficiência medida de 9 %
enquanto que a calculada através de (39) é de 8,2 % conforme mostra a Figura 21.
As Figuras 22 e 23 mostram o sistema operando com a lâmpada acesa para as
distâncias de 8 e 15 cm entre as bobinas 1 e 2.
46
Figura 22. Bobinas 1 e 2 a 8 cm de distância. Eficiência de 25 %.
Figura 23. Bobinas 1 e 2 a 8 cm de distância. Eficiência de 9 %.
47
3.3.2 SISTEMA COM 4 BOBINAS
Para o sistema de 4 bobinas a mesma metodologia foi abordada, isto é, a tensão
sobre a lâmpada foi monitorada e quando esta atinge aproximadamente 127 Vrms
considera-se que a lâmpada possui brilho máximo e dissipa a potência de 25 W.
Entretanto para este sistema devido a dificuldade de se medir as correntes nos
circuitos 1 (circuito de alta potência), 2 e 3 (não possuem resistores) apenas a
eficiência teórica foi considerada. Primeiramente fixam-se as distâncias de 15 cm
entre bobina 1 e 2, e de 8 cm entre bobina 3 e 4. A distância entre as bobinas 2 e 3
é de 30 cm. Neste caso a eficiência é de 38 % como mostra a Figura 24.
0,8
RelPow
0,7
Transf Rel. e Eff
0,6
EffCalc
0,5
0,4
0,3
0,2
0,1
0
0
20
40
d(cm)
60
80
100
Figura 24. Eficiência e transferência relativa de potência simuladas, para o sistema de 4 bobinas e
lâmpada de 25 W e 127 Vrms como carga. A distância entre a bobina 1 e 2 é de 15 cm, entre a
bobina 3 e 4 é de 8 cm.
Em seguida a distância entre as bobinas 2 e 3 é alterada para 40 cm, o que
corresponde a uma eficiência de 28 % conforme pode ser visto na Figura 24. As
Figuras 25 e 26 mostram o sistema operando para as distâncias e 30 e 40 cm entre
as bobinas 2 e 3 conforme mencionado.
48
Figura 25. Bobinas 1 e 2 a 15 cm, 3 e 4 a 8 cm, e 2 e 3 a 30 cm. Eficiência de 38 %.
Figura 26. Bobinas 1 e 2 a 15 cm, 3 e 4 a 8 cm, e 2 e 3 a 40 cm. Eficiência de 28 %.
49
4 DISCUSSÃO
Os testes apresentados na seção anterior mostram o interessante efeito de se
utilizar 4 bobinas frente ao sistema com 2 bobinas. Por exemplo, no sistema com 2
bobinas a uma distância de 15 cm tem-se eficiência de 9 %, já para o sistema com 4
bobinas alcançam-se, as distâncias de 30 e 40 cm entre bobinas 2 e 3, com
eficiências de 38 e 28 %, respectivamente, com as bobinas 1 e 2 a 15 cm e 3 e 4 a
8 cm. Ou seja, ao ajustar as distâncias entre as bobinas 1 e 2, e, 3 e 4, consegue-se
maximizar a eficiência e transferência de potência em distâncias maiores. Esse
efeito foi mostrado sobre o ponto de vista do casamento de impedâncias na seção
2.1 para o sistema com bobinas autorressonantes. Claro que em sistemas práticos,
técnicas de casamento de impedância no sistema com 2 bobinas podem melhorar a
eficiência do sistema em função da distância. Outro fator interessante no sistema
com 4 bobinas é de que esse possui máximos de eficiência e de transferência
relativa de potência. Portanto cabe ao projetista, dependendo da aplicação, definir
qual o parâmetro mais importante. Por exemplo, nota-se que o máximo de eficiência
ocorre sempre a maiores distâncias quando comparado a transferência relativa.
Portanto se o parâmetro mais importante for distância pode ser interessante projetar
o sistema de acordo com a curva de eficiência. Deve-se notar também que as
equações (36) e (50) podem alternativamente serem escritas em termos do fator de
qualidade.
50
AGRADECIMENTOS
Gostaríamos de agradecer aos professores do curso de engenharia elétrica da
PUCPR pelos ensinamentos passados, em especial ao professor Munir Antonio
Gariba pelo apoio e orientação neste projeto. Agradecemos também aos membros
da banca, professores James Alexandre Baraniuk e Gerson Linck Bichinho, pelas
sugestões que muito contribuíram para a versão final deste trabalho. Agradecemos
também aos professores da UTFPR Sérgio Francisco Pichorim e Paulo José Abatti
pelas inúmeras contribuições, bem como ao Laboratório de Biotelemetria Aplicada
(BIOTA) por oferecer a estrutura e materiais que possibilitaram o desenvolvimento
deste trabalho.
51
REFERÊNCIAS
ABATTI, P.J.; PICHORIM, S.F.; MIRANDA, C.M. “Maximum Power Transfer versus
Efficiency in Mid-Range Wireless Power Transfer Systems” IEEE Transactions on
Power Electronics. 2014 (submetido)
ABATTI, P.J.; PICHORIM, S.F.; SCHNEIDER, B. “A Method to Derive Mutual
Inductance Properties Using Electric Circuit Analysis Tools” International Journal of
Electrical Engineering Education, vol. 45, pp. 46-50, 2008.
ABNT. Limites para a Exposição a Campos Elétricos, Magnéticos e
eletromagnéticos variáveis no Tempo (até 300 GHz). PROJETO 03:077.01. 2000.
Disponível em <www.abricem2.com.br/web3/pdfs/normas/abnt31.pdf>
ARTAN, N.S ; LI, X. ; PATEL, R. ; NING, C. ; LUDVIG, N. ; CHAO, H.J. Multi-Layer
Coils for Efficient Transcutaneous Power Transfer. 33rd Annual International
Conference of the IEEE EMBS, 2011.
BREITKREUTZ, B. ; HENKE, H. Calculation of Self-Resonant Spiral Coils for
Wireless Power Transfer Systems With a Transmission Line Approach. IEEE Trans.
on Magnetics. v. 49, p. 5035-5041, 2013.
CHEON, S ; KIM Y.H ; KANG, S.Y ; LEE, M.L.L ; LEE, J.M ; ZYUNG T. CircuitModel-Based Analysis of a Wireless Energy-Transfer System via Coupled Magnetic
Resonances. IEEE Trans. on Ind. Electron. v. 58, p. 2906-2913, 2011.
CORUM, K.L ; CORUM J.F. Rf coils, helical resonators and voltage magnification by
coherent spatial modes. Microw. Rev. v. 7, p.1-10, 2001.
GOZALVEZ, J. WiTricity—The Wireless Power Transfer. IEEE Vehicular Techn.
Magaz. v. 2, p. 38-44, 2007.
HAUS, H. Waves and Fields in Optoelectronics. Prentice-Hall, Englewood Cliffs,
NJ, 1984.
HUANG W.J. ; CHEN, L.C. ; LIU, S.L. A wireless power telemetry with selfcalibrated resonant frequency. IEEE International Symposium on VLSI Design,
Automation and Test, 2009.
KO, W. H.; LIANG, S. P.; FUNG, C. D. F. Design of rafio-frequency powered coils for
implant instruments. Med. & Biol. Eng. & Comput., v. 15, p. 634-640, 1977.
KARALIS, A ; JOANNOPOLOUS, J. D ; SOLJAČIĆ, M. Efficient wireless nonradiative mid-range energy transfer. Annals of Physics, v. 323, p. 34–48, 2007.
52
KURS, A. ; KARALIS, A. ; MOFFATT, R. ; JOANNOPOULOS, J.D ; FISHER, P ;
SOLJACIC, M. “Wireless power transfer via strongly coupled magnetic resonances,”
Science, v. 317, p. 83-86, 2007.
LI, S. ; MI, C. “Wireless Power Transfer for Electric Vehicle Applications”, IEEE
Journal of Emerging and Selected Topics in Power Electronics. v. 99, p.1-4,
2014.
LI, Y. ; LI, X. ; PENG, F. ; ZHANG, H. ; GUO, W. ; ZHU, W. ; YANG, T. Wireless
Energy Transfer System Based on High Q Flexible Planar-Litz MEMS Coils 8th
IEEE International Conference on Nano/Micro Engineered and Molecular Systems
(NEMS), 2013
MARCUS, A. ; MARCUS W. Manual de Rádio. Editora Globo, Porto Alegre, 1964.
MOFFAT, R.A. Wireless Transfer of Electric Power. Master Thesis, Massachusetts
Institute of Technology, 2009.
RAMO, S ; WHINNERY, J.R ; DUZZER, T.V. Fields and Waves in Communication
Electronics. John Wiley & Sons. New York, 1965.
TESLA, Nikola. Experiments With Alternating Currents of Very High Frequency,
and Their Application to Methods of Artificial Illumination, Columbia College,
1891.
TESLA,Nikola. System of Transmission of Electrical Energy. US patent number:
645,576, 1900.
WITRICITY. Wireless Electricity Delivered Over Distance. Disponível em
<www.witricity.com> Acesso em: 28 Abr.2014.
ZHANG, F., HACKWORTH, S.A., LIU, X., CHEN, H., SCLABASSI, R.J., SUN, M.
Wireless Energy Transfer Platform for Medical Sensors and Implantable
Devices. 31st Annual International Conference of the IEEE EMBS, 2009.
ZHAO, J. ; XU, G. ; ZHANG, C. ; ZHANG, W. ; LI, X. A Contrastive Studies
between Magnetic Coupling Resonance and Electromagnetic Induction in
Wireless Energy Transmission. Sixth IEEE International Conference on
Electromagnetic Field Problems and Applications (ICEF), 2012.
ZHOU, H. ; YANG, S. Resonant Frequency Calculation of Witricity Using
Equivalent Circuit Model Combined with Finite Element Method. Sixth IEEE
International Conference on Electromagnetic Field Problems and Applications
(ICEF), 2012.