12ªaula

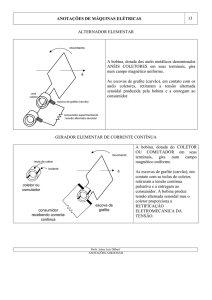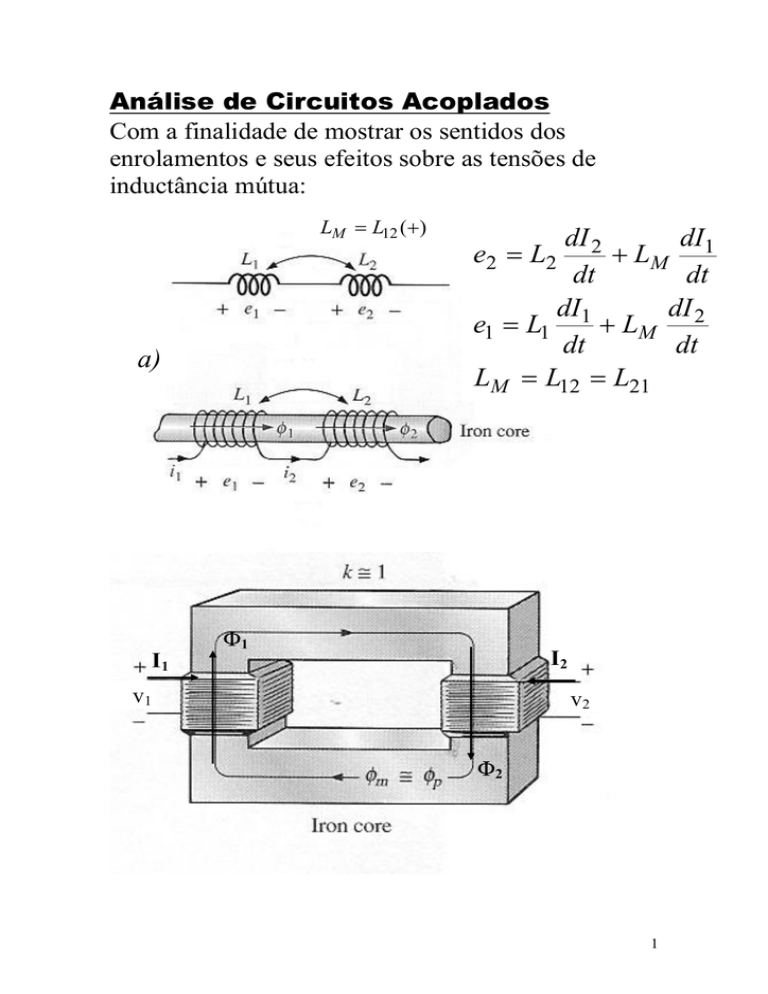
Análise de Circuitos Acoplados
Com a finalidade de mostrar os sentidos dos
enrolamentos e seus efeitos sobre as tensões de
inductância mútua:
LM = L12 (+)
a)
I1
dI 2
dI
+ LM 1
dt
dt
dI
dI
e1 = L1 1 + LM 2
dt
dt
LM = L12 = L21
e2 = L2
Φ1
I2
vv11
v2
Φ2
1
LM = L12 (−)
b)
dI 2
dI 2
dI1
dI1
e2 = L2
− LM
⇔ e1 = L1
− LM
dt
dt
dt
dt
N2
I1
v1
N1
Φ1
Φ2
I2
v2
Regra do ponto – Bobinas Acopladas.
O processo de determinação da polaridade relativa
das tensões de inductância mútua por considerações
quanto ao núcleo e ao sentido de enrolamento não é
prático !!!
Para simplificar a representação de circuitos
acoplados, as bobinas são marcadas com pontos.
2
Assim uma vez identificada a polaridade das bobinas
por intermédio de pontos, não haverá necessidade de
representar o núcleo nem o enrolamento.
Procedimento:
1. Utiliza-se a regra da mão direita para determinar
o fluxo estabelecido por cada uma das correntes.
2. Comparam-se os sentidos dos fluxos. Se são
aditivos (no mesmo sentido) coloca-se um ponto
no terminal da primeira bobina onde entra a
corrente de teste (1ª bobina). Se os fluxos
possuem sentidos contrários coloca-se um ponto
no terminal da segunda bobina onde a corrente
de teste sai.
LM (+)
LM (-)
3
Para determinar o sinal de tensão da inductância
mútua nas equações das malhas use-se a regra dos
pontos, que estabelece:
1. Quando ambas as correntes entram ou saem
de um par de bobinas acopladas pelos
terminais que têm pontos, os sinais dos
termos em LM são iguais aos sinais dos termos
em Li.
Se uma das correntes entra e a outra sai, os sinais
dos termos em LM são opostos aos dos termos em Li.
4
EXEMPLO:
Calcule a indutância total no seguinte circuito com
três bobinas em série,
Nota:
Lij = L ji
v1, 2 = L1, 2
di
di
di
di
di
di
+ L12 − L(1, 2)3 ; v3 = L3 − L23 − L13
dt
dt
dt
dt
dt
dt
5
Corrente alternada
Consideremos uma espira rectangular de área S, girando
em torno de um eixo λ em um campo magnético
uniforme, com velocidade angular ω, constante.
O fluxo de indução, Φ, através de uma superfície da
espira de área S, para uma dada posição genérica,
definida pelo ângulo α no instante t, é expresso por:
Φ = BS cos(ωt )
onde α=ωt.
6
Pela lei de Faraday:
 ωt = 1
dΦ d ( BS cos ωt )
e=
=
= ωBS sin ωt 
dt
dt
emax = ωBS
Esta fem induzida é sinosoidal ou alternada. A sua
polaridade em cada instante é determinada pela
aplicação da Lei de Lenz.
A causa que dá origem às variações de fluxo de
indução é o movimento do quadro da espira. A fem
induzida (e) faz surgir uma corrente eléctrica que
procura opôr-se a esta causa.
Durante meia volta do quadro, o fluxo de indução
aumenta e a corrente eléctrica induzida circula num
certo sentido no circuito. Durante a meia volta
seguinte, o fluxo de indução diminui e a corrente
eléctrica induzida circula em sentido contrário.
Assim a corrente eléctrica gerada é alternada e o
quadro da espira funciona como gerador de corrente
alternada.
7
Transformador
Transformador é um dispositivo electromagnético
constituído por duas bobinas independentes,
enroladas sobre um mesmo núcleo de ferro. A sua
função é transformar corrente alternada de baixa
tensão em corrente de alta tensão ou vice-versa. A
bobina que recebe a corrente a ser transformada é
denominada de enrolamento primário e, a outra
boina que fornece a corrente transformada é
denominada de enrolamento secundário.
Alguns transformadores têm vários enrolamentos
secundários, isto ocorre quando o transformador tem
de fornecer diversas tensões.
O circuito magnético é feito de ferro, a fim de
favorecer uma eficiente transmissão de fluxo, não
obstante haver pequenas perdas magnéticas, ou seja
o coeficiente de acoplamento, K=1. As linhas do
fluxo magnético vão ter o caminho de menor
relutância magnética, neste caso o núcleo de ferro!!
8
Transformador IDEAL
• Não existe dissipação de energia
• Coef. de acoplamento magnético unitário (K=1)
• Coef. de auto-indução, Lii infinito.
Pela Lei Geral de Indução,
dΦ1

v
=
N
1
 1
dt como igual fluxo atravessa as bobinas

dΦ 2
Φ1 = Φ 2 = Φ
v2 = N 2

dt
v1 N1
=
⇐ relação de transformação
v2 N 2
Lei de Ohm aplicada a circuitos magnéticos:
ℑ = ℜΦ ⇔ N1I1 + N 2 I 2 = ℜΦ
caso ideal:
I
N
ℜ m = 0 ⇔ N1I1 + N 2 I 2 = 0 ⇔ 1 = − 2
I2
N1
I
v1 N1
Potência cedida
=
= − 2 ⇔ v1I1 = −v2 I 2
ao secundario
v2 N 2
I1
Potência fornecida ao prímario
di1
di2

v
=
L
+
L
1
M
 1
dt
dt não são válidas
As equações 
di
di
v2 = LM 1 + L2 2

dt
dt
L
quando a ligação magnética é K = M = 1.
L1L2
9
v1 N1

=

AS equações válidas são: 
v2 N 2
 N1I1 + N 2 I 2 = 0
v1 v2 N1 − N1
v2 N12
=
=−
I1
N 2 N2I2
I 2 N 22
R1 = − R2
N12
N 22
O transformador ideal é um
elemento resistivo.
Se se ligar uma resistência ao enrolamento 2, a
resistência no enrolamento 1 é:
R1
R22
R1 = −
N P2
N S2
R2
10