1. (Pucrj 2015) Um bloco de gelo se encontra em

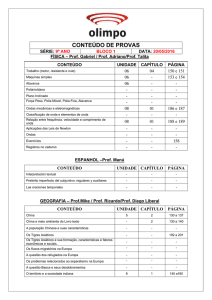
1. (Pucrj 2015) Um bloco de gelo se encontra em repouso no alto de uma rampa sem
atrito, sendo sustentado por uma força horizontal F de módulo 11,6 N, como mostrado
na figura.
Dados:
g  10m s2
sen 30  0,50
cos 30  0,87
a) Calcule a massa do bloco de gelo.
b) Considere agora que a força F deixe de atuar. Calcule a velocidade com que o bloco
chegaria à base da rampa, após percorrer os 6,4 m de sua extensão.
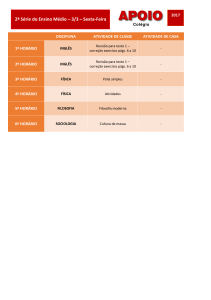
2. (Pucrj 2013) Na figura abaixo, o bloco 1, de massa m1 = 1,0 kg, havendo partido do
repouso, alcançou uma velocidade de 10 m/s após descer uma distância d no plano
inclinado de 30°. Ele então colide com o bloco 2, inicialmente em repouso, de massa m2
= 3,0 kg. O bloco 2 adquire uma velocidade de 4,0 m/s após a colisão e segue a
trajetória semicircular mostrada, cujo raio é de 0,6 m. Em todo o percurso, não há atrito
entre a superfície e os blocos. Considere g = 10 m/s2.
a) Ao longo da trajetória no plano inclinado, faça o diagrama de corpo livre do bloco 1 e
encontre o módulo da força normal sobre ele.
b) Determine a distância d percorrida pelo bloco 1 ao longo da rampa.
c) Determine a velocidade do bloco 1 após colidir com o bloco 2.
d) Ache o módulo da força normal sobre o bloco 2 no ponto mais alto da trajetória
semicircular.
3. (Pucrj 2012) Um arqueiro se prepara para lançar uma flecha de massa 100 g da borda
de um precipício, de altura H = 320 m, utilizando uma balestra. O arqueiro retesa as
cordas da balestra, que podemos supor como sendo um sistema de molas com um
coeficiente k = 1440 N/m, para lançar horizontalmente a flecha que segue a trajetória
representada na figura abaixo.
Dados: a resistência do ar é desprezível e g = 10 m/s2
a) Dado que o arqueiro puxa as cordas por d = 30 cm, calcule a velocidade de saída da
flecha.
b) Calcule o intervalo de tempo necessário para que a flecha caia no chão abaixo.
c) Calcule a distância horizontal D percorrida pela flecha até tocar o chão.
4. (Pucrj 2010) Alberto (A) desafiou seu colega Cabral (C) para uma competição de
cabo de guerra, de uma maneira especial, mostrada na figura. Alberto segurou no
pedaço de corda que passava ao redor da polia enquanto que Cabral segurou no pedaço
atado ao centro da polia. Apesar de mais forte, Cabral não conseguiu puxar Alberto, que
lentamente foi arrastando o seu adversário até ganhar o jogo. Sabendo que a força com
que Alberto puxa a corda é de 200 N e que a polia não tem massa nem atritos:
a) especifique a tensão na corda que Alberto está segurando;
b) desenhe as forças que agem sobre a polia, fazendo um diagrama de corpo livre;
c) calcule a força exercida pelo Cabral sobre a corda que ele puxava;
d) considerando que Cabral foi puxado por 2,0 m para frente, indique quanto Alberto
andou para trás.
5. (Pucrj 2009) Um brinquedo de parque de diversões consiste (veja as figuras a seguir)
de um eixo vertical girante, duas cabines e um suporte para os cabos que ligam o eixo às
cabines. O suporte é uma forte barra horizontal de aço, de L = 8,0 m de comprimento,
colocada de modo simétrico para poder sustentar as cabines. Cada cabo mede d = 10 m.
Quando as pessoas entram nas cabines, o eixo se põe a girar e as cabines se inclinam
formando um ângulo ? com a vertical. O movimento das cabines é circular uniforme,
ambos de raio R. Considere a massa total da cabine e passageiro como M = 1000 kg.
Suponha que è = 30°. Considere g = 10 m/s2 para a aceleração gravitacional e despreze
todos os efeitos de resistência do ar.
a) Desenhe na figura anterior o raio R de rotação, para a trajetória da cabine do lado
direito, e calcule seu valor.
b) Desenhe na figura anterior as forças agindo sobre a cabine do lado esquerdo. Qual a
direção e o sentido da força resultante Fr sobre esta cabine?
c) Sabendo que as forças verticais sobre a cabine se cancelam, calcule a tensão no cabo
que sustenta a cabine.
d) Qual o valor da força centrípeta agindo sobre a cabine?
Gabarito:
Resposta da questão 1: a) De acordo com o diagrama de forças abaixo representado:
Para o eixo horizontal:
F  Nx  N  sen 30 (1)
Para o eixo vertical:
Ny  P  N  cos 30  m  g
N
mg
(2)
cos 30
Substituindo (2) em (1):
F
mg
 sen 30
cos 30
Explicitando a massa:
m
F

g  tan 30
11,6 N
3
10 m / s 
3
 m  2 kg
2
b) A velocidade na base da rampa é calculada pela equação de Torricelli após
determinarmos a aceleração devida à componente do peso Pz decomposta na direção do
plano inclinado.
Pz  m  g  sen 30
a
Pz
 g  sen 30  10 m / s2  0,5  5 m / s2
m
Pro Torricelli:
v 2  v02  2aΔs  v  v02  2aΔs
v  0  2  5 m / s2  6,4 m  v  8 m / s
Resposta da questão 2: Em toda a questão o atrito será desprezado
a) Observando a figura abaixo podemos concluir que N  Pcos30  10
3
 5 3N.
2
b) Pela conservação da energia.
mgdsen30 
1
mV2  10xdx0,5  0,5x102  d  10 m
2
c) Pela conservação da quantidade de movimento na colisão, vem:
m1V1  m2 V2  m1  V0 1  m2  V0 2
1xV1  3x4  1x10  3x0  V1  10  12  2,0m / s
d) As figuras abaixo mostram as posições inicial e final do bloco 2 e as forças que agem
sobre ele no topo da lombada.
Podemos determinar V pela Conservação da energia.
1
1
mV 2  mgH  mV02  V 2  2gH  V02
2
2
1 2
1
V  10x0,6  x42  V 2  4
2
2
A força centrípeta no topo da trajetória vale:
P N  m
V2
4
 30  N  3x
 30  N  20  N  10N
R
0,6
Resposta da questão 3:
a) Dados: k = 1.440 N/m; d = 30 cm = 0,3 m; m = 100 g = 0,1 kg.
Pela conservação da energia mecânica, a energia potencial elástica armazenada na
balestra é transformada em cinética na flecha:
mv 2 k d2

2
2
v  36 m /s.
 vd
k
1.440
 v  0,3
 0,3 14.400  0,3 120  
m
0,1
b) Dados: H = 320 m; g = 10 m/s2.
O tempo de voo do lançamento horizontal é igual ao tempo de queda livre. Então:
H
1
g t2
2
 t
2 H

g
2  320 
10
 64 
t  8 s.
c) Dos itens anteriores: v = 36 m/s; t = 8 s.
Na horizontal, o movimento é uniforme:
D  v t  36  8   D  288 m.
Resposta da questão 4:
a) A tensão (ou tração, que é o termo mais adequado) na corda corresponde à
intensidade da força aplicada por Alberto: T = 200 N.
b) F : força de tração no centro da polia, aplicada por Cabral;
T : forças aplicadas pela corda que passa pela polia.
c) Como a polia não tem massa (ou seja, sua massa é desprezível) e, além disso, ela está
sendo arrastada quase-estaticamente (ou seja, com velocidade constante  a = 0),
aplicando o princípio fundamental, temos:
F – 2 T = m a  F – 2 T = 0  F = 2 T = 2 (200)  F = 400 N.
d) A figura a seguir mostra que quando a ponta da corda desloca D (do ponto do ponto
P até o ponto P’ ), o centro da polia desloca D/2.
Assim, se corda que Alberto puxa enrola D, essa distância é distribuída nos dois braços
da polia, fazendo com o seu centro desloque D/2. Portanto, se Carlos avança 2 m,
Alberto recua 4 m.
Resposta da questão 5:
8
R = (L/2) + d.sen =   + 10.sen30 = 4 + 10.0,5 = 4 + 5 = 9 m
2
Na figura
T.cos = M.g  T.cos30 = 1000.10  T.0,87 = 10000  T =
10000
= 11494 N
0,87
A resultante centrípeta atua no plano horizontal, logo: Fcentrípeta = T.sen30 =
11494.0,5 = 5747 N