ângulos e arcos na circunferência

Prof° André Costa de Oliveira.
1° Ano do Ensino médio;
Trigonometria:
Introdução: ângulos e arcos na circunferência;
Ângulo central: É todo ângulo que possui o seu vértice no centro da circunferência, o
arco determinado por dois raios e o ângulo central, possui a mesma medida do ângulo
central;
Ângulo inscrito: É todo ângulo que possui origem no vértice, e seus lados serão
secantes a circunferência, a medida deste será sempre metade do arco estabelecido por
ele;
Ângulo de segmento: É todo aquele cujo vértice pertence a circunferência, onde um
dos lados é secante e o outro tangente, sua medida é metade do arco por ele
estabelecido;
Ângulo excêntrico interior
Ângulo excêntrico interior é aquele ângulo que possui como vértice um ponto longe
do centro da região interior da circunferência.
Na figura, o ângulo APB é excêntrico interior e estabelece na circunferência o arco
AB.
As retas PA e PB interceptam a circunferência nos pontos C e D,
estabelecendo o arco CD. A medida do ângulo APB é a metade da soma dos arcos AB e
CD.
Logo:
Logo:
Ângulo excêntrico exterior
Ângulo excêntrico exterior é aquele ângulo que possui como vértice um ponto da
região exterior da circunferência, e lados secantes ou tangentes à circunferência.
Na figura, o ângulo APB é excêntrico exterior e determina na circunferência os arcos
AB e CD.
A medida do ângulo APB é a metade da diferença entre os arcos AB e CD.
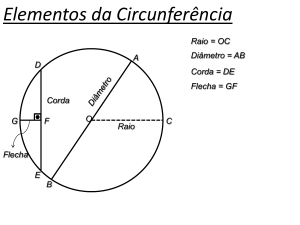
Arcos de circunferência:
Na determinação dos arcos de uma circunferência podemos ter dois tipos de
medições: a linear e a angular. A medida linear de um arco qualquer é a distância entre
dois pontos A e B, postulados na extremidade da circunferência. Observe:
Com base na ilustração notamos que a medida do arco AB é igual à medida da reta EF
(arco esticado), e a medida angular do arco AB corresponde à medida do ângulo central
do arco, ou seja, a medida angular do arco AB é a mesma medida do ângulo
central: m(AB) = m(AÔB). Para representar a medida angular de arcos de
circunferência, utilizamos as seguintes unidades: grau e radiano.
Graus
A medida em graus de uma circunferência consiste em dividi-lá em 360 partes
congruentes entre si, dessa forma, cada parte equivalerá a um arco de medida igual a 1º
(um grau). Se dividirmos esse arco de 1º em 60 partes teremos cada parte medindo
1’(um minuto) e esse arco de 1’ minuto dividido em 60 partes iguais formam arcos
correspondentes a 1” (um segundo). Assim, concluímos que: 1º = 60’ e 1’= 60”.
Radianos
Outra unidade de medida de arcos muito usual é o radiano, que consiste no arco cujo
comprimento é igual à medida do raio da circunferência que o contém. Por exemplo, um
arco de 3 rad corresponde ao arco de comprimento igual a 3 raios da circunferência,
veja:
Comprimento AB = 3r → m(AB) = m(AÔB) = 3 rad
Ao dividirmos o comprimento do arco (l) de uma circunferência pelo seu raio (r),
determinamos a medida do ângulo central em radianos.
Existe uma relação entre as medidas em grau e radiano, podemos destacar a seguinte
relação:
360º → 2π radianos (aproximadamente 6,28)
180º → π radiano (aproximadamente 3,14)
90º → π/2 radiano (aproximadamente 1,57)
45º → π/4 radiano (aproximadamente 0,785)
As medidas de arcos de circunferências em graus e em radianos são diretamente
proporcionais, dessa forma podemos realizar as conversões utilizando uma regra de três
simples:
Medida em graus
Medida em radianos
x
α
180
π
Exemplo:
1) Faça as seguintes transformações:
a) 100º em radianos
b) 7π/15 rad em graus
O ciclo trigonométrico: O ciclo trigonométrico é uma circunferência orientada, com
raio unitário, associada a um sistema de coordenadas cartesianas. O centro da
circunferência coincide com a origem do sistema cartesiano. Dessa forma, o círculo fica
dividido em quatro quadrantes identificados de acordo com o sentido anti-horário a
partir do ponto A, para valores positivos e sentido horário para valores negativos.
Valoração por quadrantes:
Primeiro quadrante: 0º < x < 90º
Segundo quadrante: 90º < x < 180º
Terceiro quadrante: 180º < x < 270º
Quarto quadrante: 270º < x < 360º
Os valore, podem também, ser apresentados em outra medida chamada de radianos:
Primeiro quadrante: 0 < x < π/2
Segundo quadrante: π/2 < x < π
Terceiro quadrante: π < x < 3π/2
Quarto quadrante: 3π/2 < x < 2π
Arcos com mais de uma volta
Em Trigonometria, algumas vezes precisamos considerar arcos cujas medidas sejam
maiores do que 360º. Por exemplo, se um ponto móvel parte de um ponto A sobre uma
circunferência no sentido anti-horário e para em um ponto M, ele descreve um arco AM.
A medida deste arco (em graus) poderá ser menor ou igual a 360º ou ser maior do
que 360º. Se esta medida for menor ou igual a 360º, dizemos que este arco está em
sua primeira determinação.
Acontece que o ponto móvel poderá percorrer a circunferência uma ou mais vezes em
um determinado sentido, antes de parar no ponto M, determinando arcos maiores do que
360º ou arcos com mais de uma volta. Existe uma infinidade de arcos mas com medidas
diferentes, cuja origem é o ponto A e cuja extremidade é o ponto M.
Seja o arco AM cuja primeira determinação tenha medida igual a m. Um ponto móvel
que parte de A e pare em M, pode ter várias medidas algébricas, dependendo do
percurso.
Se o sentido for o anti-horário, o ponto M da circunferência trigonométrica será
extremidade de uma infinidade de arcos positivos de medidas:
m, m+2 , m+4 , m+6 , ...
Se o sentido for o horário, o ponto M será extremidade de uma infinidade de arcos
negativos de medidas algébricas:
m-2 , m-4 , m-6 , ...
E temos assim uma coleção infinita de arcos com extremidade no ponto M.
Generalizando este conceito, se m é a medida da primeira determinação positiva do
arco AM, podemos representar as medidas destes arcos por:
µ(AM) = m + 2k
Onde k é um número inteiro, isto é, k pertence ao conjunto Z={...,-2,-3,-1,0,1,2,3,...}.
Família de arcos: Uma família de arcos {AM} é o conjunto de todos os arcos com
ponto inicial em A e extremidade em M.
Exemplo: Se um arco de circunferência tem origem em A e extremidade em M, com a
primeira determinação positiva medindo 2 /3, então os arcos desta família {AM},
medem:
k=0
k=1
k=2
k=3
...
k=n
k=-1
k=-2
k=-3
k=-4
...
k=-n
Determinações positivas (sentido anti-horário)
µ(AM)=2 /3
µ(AM)=2 /3+2 =8 /3
µ(AM)=2 /3+4 =14 /3
µ(AM)=2 /3+6 =20 /3
...
µ(AM)=2 /3+2n =(2+6n) /3
Determinações negativas (sentido horário)
µ(AM)=2 /3-2 =-4 /3
µ(AM)=2 /3-4 =-6 /3
µ(AM)=2 /3-6 =-16 /3
µ(AM)=2 /3-8 =-22 /3
...
µ(AM)=2 /3-2n =(2-6n) /3
Arcos côngruos e Ângulos
Arcos côngruos: Dois arcos são côngruos se a diferença de suas medidas é um
múltiplo de 2 .
Exemplo: Arcos de uma mesma família são côngruos.
Expressão geral dos arcos côngruos
 Graus: x = x0 + 360°.k, onde k ∈ Z e 0º ≤ x0 < 360º
 Radianos: x = x0 + k.2π, onde k ∈ Z e 0 ≤ x0 < 2π
Em ambos os casos, x0 é denominado primeira determinação positiva e k é o número
de voltas.
Exemplo:
(UFPA) A menor determinação positiva de um arco de 1000º é:
a) 270º
b) 280º
c) 290º
d) 300º
e) 310º
Solução:
Dividindo 1000 por 360 obtemos quociente igual a 2 e resto igual a 280. Assim,
podemos escrever:
1000° = 2.360° + 280°
ou
1000° = 280° + 2.360°
Neste caso, x0 = 280°. Portanto, letra b.
Ângulos: As noções de orientação e medida algébrica de arcos podem ser estendidas
para ângulos, uma vez que a cada arco AM da circunferência trigonométrica
corresponde a um ângulo central determinado pelas semirretas OA e OM.
Como no caso dos arcos, podemos considerar dois ângulos orientados um positivo
(sentido anti-horário) com medida algébrica a correspondente ao arco AM e outro
negativo (sentido horário) com medida b=a-2 correspondente ao arco AM.
Existem também ângulos com mais de uma volta e as mesmas noções apresentadas
para arcos se aplicam para ângulos.
Arcos de mesma origem, simétricos em relação ao eixo OX
Sejam os arcos AM e AM' na circunferência trigonométrica, com A=(1,0) e os pontos
M e M' simétricos em relação ao eixo horizontal OX. Se a medida do arco AM é igual a
m, então a medida do arco AM' é dada por: µ(AM')=2 -m.
Os arcos da família {AM}, aqueles que têm origem em A e extremidades em M, têm
medidas iguais a 2k +m, onde k é um número inteiro e os arcos da família {AM'} têm
medidas iguais a 2k -m, onde k é um número inteiro.
Arcos de mesma origem, simétricos em relação ao eixo OY
Sejam os arcos AM e AM' na circunferência trigonométrica com A=(1,0) e os pontos
M e M' simétricos em relação ao eixo vertical OY. Se a medida do arco AM for igual a
m, então a medida do arco AM' será dada pela expressão µ(AM')= -m.
Os arcos da família {AM'}, isto é, aqueles com origem em A e extremidade em M',
medem 2k + -m=(2k+1) -m onde k é um número inteiro.
Arcos com a mesma origem e extremidades simétricas em relação à origem
Sejam os arcos AM e AM' na circunferência trigonométrica com A=(1,0) e os pontos
M e M' simétricos em relação a origem (0,0).
Se a medida do arco AM é igual a m, então a medida do arco AM' é dada por:
µ(AM')= +m. Arcos genéricos com origem em A e extremidade em M' medem:
µ(AM') = 2k
+
+ m = (2k+1)
+m