III-1 – Comprimento de Arco

III-1 – Comprimento de Arco
Nesta aula vamos iniciar com o tratamento de integral que não calcula apenas área sob uma
curva. Especificamente, o processo ainda é unidimensional, mas envolve conceitos de
geometria (especificamente trigonometria) e possibilita a realização do cálculo de comprimento
de uma curva. Esta prática permite determinar-se perímetro de terrenos que não possuem
traçados regulares, mas podem ser definidos por uma função. Além disso, na prática, acena
para o cálculo de momento de inércia e centróide de objetos do tipo arame, fio, etc. que não
possuem geometria bem definida.
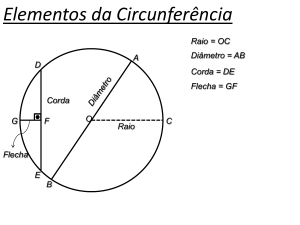
O comprimento de um arco AB de uma curva, por definição, é o limite da soma dos
comprimentos consecutivos de corda, AP1, P1P2, P2P3... Pn-1,Pn, ligando os pontos no arco,
quando o número de pontos cresce indefinidamente de tal modo que o comprimento de cada
corda tenda a zero.
y
𝑃3
Pn-1 B
P3
A
𝑃2
P1
P2
x
Observe na figura que o comprimento
P3, portanto:
é a hipotenusa do triângulo que une os pontos P2 e
Se A(a,c), e B(b,d) são dois pontos da curva
, onde
contínuas no intervalo [a,b], o comprimento de arco AB é dado por:
Analogamente, se A (a,c) e B (b,d) são dois pontos da curva
continuas e [c,d] o comprimento de arco AB é dado por:
e sua derivada
, onde
e
são
são
III-1 – Comprimento de Arco
Se A (u=u1) e B(u=u2) são dois pontos de uma curva definida pelas equações paramétricas
e se as condições de continuidade são satisfeitas, o comprimento de arco
AB é dado por:
Exemplo 1:
Achar o comprimento da reta no
intervalo [0,1]. O gráfico da reta é:
y
Y=2x+2
4
2
1
x
A derivada da função:
Aplicando na equação para x.
Neste mesmo exemplo pode-se calcular o comprimento da curva em relação a y. Nesse caso o
intervalo deve ser [2,4] e a função pode ser invertida, ou seja:
Daí,
III-1 – Comprimento de Arco
Outra maneira de se encontrar a derivada é diferenciando-se a função e, portanto:
Aplicando a equação do comprimento de arco.
Portanto:
Outro caminho é fazer os cálculos através das curvas paramétricas. Vamos resolver o
problema criando duas funções paramétricas a partir da função
Para isto pode-se
fazer o seguinte:
O intervalo em
é:
Calculando as derivadas:
III-1 – Comprimento de Arco
Aplicando a equação para as curvas paramétricas.
Observa-se, que geometricamente o comprimento da curva é
como é destacado na figura e, portanto:
Vejamos alguns exemplos mais complexos.
Exemplo 2:
Ache o comprimento do arco de curva:
O intervalo é:
Substituindo na fórmula paramétrica:
Substituindo os limites de integração tem-se:
pois é um triângulo retângulo
III-1 – Comprimento de Arco
Exemplo 3:
Dado um círculo de raio R, determine o seu comprimento duas formas.
a) Utilizando a função
.
b) Parametrizando as funções
Onde
é o ângulo formado com o eixo x.
y
y
R

x
x
a) Inicialmente deve-se criar a função. Olhando para o circulo, pode-se determinar o
comprimento do raio.
Isolando
temos:
Derivando-se
em relação a .
O intervalo de integração será de – até , que deve dar o comprimento do semicírculo. Para
o comprimento total, basta multiplicar este resultado por 2 (dois). Portanto.
III-1 – Comprimento de Arco
Esta integral deve ser resolvida por substituição trigonométrica.
Observando o círculo define-se:
Para:
Substituindo na integral:
Observe que o resultado é o correspondente ao comprimento da circunferência conhecido.
b)
Neste caso vamos parametrizar x e y à variável . No gráfico do circulo vê-se.
Então:
Para o comprimento do circulo
deve variar de 0 a 2 e portanto:
III-1 – Comprimento de Arco
, relação trigonométrica fundamental.
Observe que parametrizando x e y, a resolução fica mais simples e sem muita substituição. A
matemática (o cálculo) tem disso, é necessário possuir experiência e desenvolver o raciocínio
logico para resolver problemas com eficiência e eficácia.
Nesse sentido, além de aprender cálculo, o aluno desenvolve habilidades e competências que
serão positivas na vida profissional.