Plano de Trabalho Docente – PTD

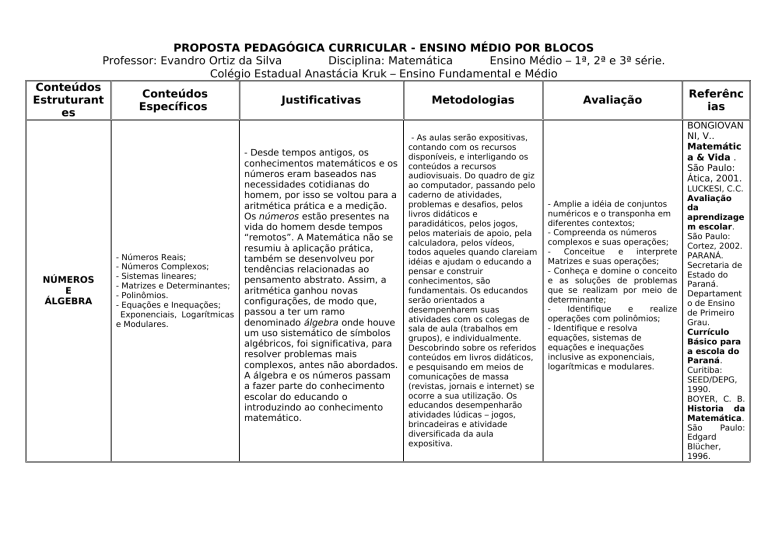
PROPOSTA PEDAGÓGICA CURRICULAR - ENSINO MÉDIO POR BLOCOS
Professor: Evandro Ortiz da Silva
Disciplina: Matemática
Ensino Médio – 1ª, 2ª e 3ª série.
Colégio Estadual Anastácia Kruk – Ensino Fundamental e Médio
Conteúdos
Estruturant
es
NÚMEROS
E
ÁLGEBRA
Conteúdos
Específicos
-
Números Reais;
Números Complexos;
Sistemas lineares;
Matrizes e Determinantes;
Polinômios.
Equações e Inequações;
Exponenciais, Logarítmicas
e Modulares.
Justificativas
- Desde tempos antigos, os
conhecimentos matemáticos e os
números eram baseados nas
necessidades cotidianas do
homem, por isso se voltou para a
aritmética prática e a medição.
Os números estão presentes na
vida do homem desde tempos
“remotos”. A Matemática não se
resumiu à aplicação prática,
também se desenvolveu por
tendências relacionadas ao
pensamento abstrato. Assim, a
aritmética ganhou novas
configurações, de modo que,
passou a ter um ramo
denominado álgebra onde houve
um uso sistemático de símbolos
algébricos, foi significativa, para
resolver problemas mais
complexos, antes não abordados.
A álgebra e os números passam
a fazer parte do conhecimento
escolar do educando o
introduzindo ao conhecimento
matemático.
Metodologias
- As aulas serão expositivas,
contando com os recursos
disponíveis, e interligando os
conteúdos a recursos
audiovisuais. Do quadro de giz
ao computador, passando pelo
caderno de atividades,
problemas e desafios, pelos
livros didáticos e
paradidáticos, pelos jogos,
pelos materiais de apoio, pela
calculadora, pelos vídeos,
todos aqueles quando clareiam
idéias e ajudam o educando a
pensar e construir
conhecimentos, são
fundamentais. Os educandos
serão orientados a
desempenharem suas
atividades com os colegas de
sala de aula (trabalhos em
grupos), e individualmente.
Descobrindo sobre os referidos
conteúdos em livros didáticos,
e pesquisando em meios de
comunicações de massa
(revistas, jornais e internet) se
ocorre a sua utilização. Os
educandos desempenharão
atividades lúdicas – jogos,
brincadeiras e atividade
diversificada da aula
expositiva.
Avaliação
Referênc
ias
BONGIOVAN
NI, V..
Matemátic
a & Vida .
São Paulo:
Ática, 2001.
- Amplie a idéia de conjuntos
numéricos e o transponha em
diferentes contextos;
- Compreenda os números
complexos e suas operações;
Conceitue
e
interprete
Matrizes e suas operações;
- Conheça e domine o conceito
e as soluções de problemas
que se realizam por meio de
determinante;
Identifique
e
realize
operações com polinômios;
- Identifique e resolva
equações, sistemas de
equações e inequações
inclusive as exponenciais,
logarítmicas e modulares.
LUCKESI, C.C.
Avaliação
da
aprendizage
m escolar.
São Paulo:
Cortez, 2002.
PARANÁ.
Secretaria de
Estado do
Paraná.
Departament
o de Ensino
de Primeiro
Grau.
Currículo
Básico para
a escola do
Paraná.
Curitiba:
SEED/DEPG,
1990.
BOYER, C. B.
Historia da
Matemática.
São
Paulo:
Edgard
Blücher,
1996.
GRANDEZAS
E
MEDIDAS
FUNÇÕES
- Medidas de área;
- Medidas de Volume;
- Medidas de Grandezas
Vetoriais;
- Medidas de Informática;
- Medidas de Energia;
- Trigonometria.
-
Função Afim;
Função Quadrática;
Função Polinomial;
Função Exponencial;
Função Logarítmica;
Função Trigonométrica;
Função Modular;
Progressão Aritmética;
Progressão Geométrica.
- Desde a Antigüidade, o homem se
deparou com noções de maior e
menor, de antes e depois e com isso
passou a realizar comparações entre
espaços e entre períodos de tempo,
estabelecendo valores qualitativos e
quantitativos, o ser humano precisou
medir e criar instrumentos de
medida. As medidas se tornaram a
linguagem fundamental à realização
dos negócios no mundo do comércio.
Elas podem ser consideradas um dos
principais fatores que sustentaram e
fortaleceram as sociedades pelas
relações estabelecidas por meio das
compras e vendas, pela criação dos
padrões que mensuram a produção
e pelo suporte dimensional para as
ciências e a tecnologia, portanto, se
tornando essencial para o educando.
O aprimoramento dos instrumentos
de medida inspirou matemáticos a
estudarem as noções de funções
pela experiência e observação, o que
contribuiu para a evolução do
conceito. Desenvolveram-se, então,
o tratamento quantitativo,
simbolizou os primeiros sinais de
modernização do ensino de
Matemática. As Funções devem ser
vistas como construção histórica e
dinâmica, capaz de provocar
mobilidade às explorações
matemáticas, por conta da
variabilidade e da possibilidade de
análise do seu objeto de estudo e
por sua atuação em outros
conteúdos específicos da
Matemática. Tal mobilidade oferece
ao aluno a noção analítica de leitura
do objeto matemático.
- As aulas serão expositivas,
contando com os recursos
disponíveis, e interligando os
conteúdos a recursos
audiovisuais. Os educandos
serão orientados a
desempenharem suas
atividades com os colegas de
sala de aula (trabalhos em
grupos), e individualmente.
Descobrindo sobre os referidos
conteúdos em livros didáticos,
e pesquisando em meios de
comunicações de massa
(revistas, jornais e internet) se
ocorre a sua utilização.
- As aulas serão expositivas,
contando com os recursos
disponíveis, e interligando os
conteúdos a recursos
audiovisuais. Do quadro de giz
ao computador, passando pelo
caderno de atividades,
problemas e desafios, pelos
livros didáticos e
paradidáticos, pelos jogos,
pelos materiais de apoio, pela
calculadora, pelos vídeos,
todos aqueles quando clareiam
idéias e ajudam o educando a
pensar e construir
conhecimentos. Descobrindo
sobre os referidos conteúdos
em livros didáticos, e
pesquisando em meios de
comunicações de massa
(revistas, jornais e internet) se
ocorre a sua utilização.
FRANÇA, E. (et
al.)
Matemática
na vida e na
escola. São
Paulo: Brasil,
1999. Obra em
- Perceba que as unidades de
4v.
medidas são utilizadas para a SOUZA, M.H.S.
determinação de diferentes
Matemática:
grandezas;
livro do
- Compreenda a relações
professor.
matemáticas existentes nas
São Paulo,
unidades de medida de
Ática 2002.
diversas grandezas;
DANTE, L. R.
- Aplique a lei dos senos e a lei
Tudo é
dos cossenos de um triângulo
Matemática.
qualquer para determinar
São Paulo:
elementos desconhecidos.
Ática, 2002.
coleção em
4v.
- Identifique diferentes
funções;
- Realize cálculos envolvendo
diferentes funções;
- Aplique os conhecimentos
sobre funções para resolver
situações-problema;
- Realize análise gráfica de
diferentes funções;
- Reconheça nas seqüências
numéricas, particularidades
que remetem ao conceito das
progressões aritméticas e
geométricas;
- Generalize cálculos para a
determinação de termos de
uma seqüência numérica.
Coleção
Matemática
Completa.
GIOVANNI E
BONJORNO
2ª Edição
renovada .
São Paulo
2005.
GEOMETRIAS
TRATAMENTO
DA
INFORMAÇÃO
- Geometria Plana;
- Geometria Espacial;
- Geometria Analítica;
Geometria
NãoEuclidiana.
-
Analise Combinatória;
Binômio de Newton;
Estudo das Probabilidades;
Estatística;
Matemática Financeira.
- As idéias geométricas abstraídas das
formas da natureza que aparecem tanto
na vida inanimada como na vida orgânica
e nos objetos produzidos pelas diversas
culturas, influenciaram muito o
desenvolvimento humano. A geometria
não deve ser rigidamente separada da
aritmética e da álgebra, pois ambas
estão interligadas e fazem parte da vida.
Portanto, deve ser considerada de
relevância para a vida do educando.
- A Estatística, então, tornou-se um
conteúdo matemático importante ao
ter seus conceitos aplicados em
vários campos do conhecimento. O
tratamento da informação é um
conteúdo estruturante que contribui
para o desenvolvimento de
condições de leitura crítica dos fatos
ocorridos na sociedade e para
interpretação de tabelas e gráficos
que, de modo geral, são usados para
apresentar ou descrever
informações. É o educando que
busca, seleciona, faz conjecturas,
analisa e interpreta as informações
para, em seguida, apresentá-las para
o grupo, sua classe ou sua
comunidade, dando uma aplicação
para a matemática aprendida em
sala de aula.
- As aulas serão expositivas,
contando com os recursos
disponíveis, e interligando os
conteúdos a recursos audiovisuais.
Do quadro de giz ao computador,
passando pelo caderno de
atividades, problemas e desafios,
pelos livros didáticos e
paradidáticos, pelos jogos, pelos
materiais de apoio, pela
calculadora, pelos vídeos, todos
aqueles quando clareiam idéias e
ajudam o educando a pensar e
construir conhecimentos, são
fundamentais. Os educandos serão
orientados a desempenharem suas
atividades com os colegas de sala
de aula (trabalhos em grupos), e
individualmente. Descobrindo
sobre os referidos conteúdos em
livros didáticos, e pesquisando em
meios de comunicações de massa
(revistas, jornais e internet) se
ocorre a sua utilização.
- Amplie aprofunde nos
conceitos geométricos em um
nível abstrato mais complexo;
- Realize análise dos
elementos que estruturam as
geometrias;
- Perceba a necessidade das
geometrias não-Euclidianas
para a compreensão de
conceitos geométricos, quando
analisados em planos
diferentes do plano de
Euclides;
- Compreenda a necessidade
das geometrias nãoEuclidianas para o avanço das
teorias científicas;
- Articule idéias geométricas
em planos de curvatura nula,
positiva e negativa;
- Conheça os conceitos básicos
da Geometria Elíptica, da
Geometria Hiperbólica e da
Geometria Fractal.
- As aulas serão expositivas, do
quadro de giz ao computador,
passando pelo caderno de
atividades, problemas e
desafios, pelos livros didáticos,
pelos jogos, pelos materiais de
apoio, pela calculadora, pelos
vídeos, todos aqueles quando
clareiam idéias e ajudam o
educando a pensar e construir
conhecimentos, são
fundamentais. Os educandos
serão orientados a
desempenharem suas
atividades com os colegas de
sala de aula e individualmente.
Descobrindo sobre os referidos
conteúdos em livros didáticos,
e pesquisando em meios de
comunicações de massa
(revistas, jornais e internet) se
ocorre a sua utilização.
- Manuseie dados desde sua
coleta até os cálculos que
permitirão tirar conclusões e a
formulação de opiniões;
- Domine os conceitos do
conteúdo Binômio de Newton;
- Saiba tratar a informações e
compreenda a idéia de
probabilidade;
- Realize estimativas,
conjecturas a respeito de
dados e informações
estatísticas;
- Compreenda a Matemática
Financeira aplicada ao diversos
ramos da atividade humana;
- Perceba, através da leitura,
construção e interpretação de
gráficos, a transição da
álgebra para a representação
gráfica e vice-versa.
Observações: Os conteúdos foram divididos em bimestres – I primeiro e II segundo bimestres.
1ª Série
1º Bimestre - 2011
Conjuntos
2º Bimestre - 2011
Função Exponencial
-Representação de um conjunto;
-Pertinência;
-Igualdade;
-União e intersecção de conjuntos;
-Aplicação da teoria dos conjuntos na
resolução de alguns problemas;
Função do 1º Grau
- Potenciação
- Propriedades da potenciação;
- Expoente negativo e por fração;
- Função exponencial;
- Equação exponencial;
Logaritmos
- Função constante;
- Função identidade;
- Função do 1º grau e seus coeficientes;
- Raiz ou zero da função;
- Gráfico da função com a raiz e o coeficiente
Linear;
Função Quadrática
-
Função quadrática;
Raízes da função quadrática;
Gráfico da função quadrática;
Concavidade da parábola;
Vértice da parábola,
Imagem;
Ponto de mínimo e de máximo de
uma função;
- Condição de existência do logaritmo;
- Propriedades decorrentes e operatórias;
- Mudança de base;
- Função logarítmica;
Progressões
- Progressão aritmética;
- Fórmula do termo geral da P.A;
- Propriedades;
- Soma dos termos de uma P.A;
- Fórmula do termo geral P.G;
- Propriedades;
- Soma dos termos de uma P.G;
Trigonometria
-
Razões trigonométrica no triângulo retângulo
Tabela de razões trigonométricas de ângulos;
Circunferência trigonométrica
Arcos e ângulos;
2ª série
1° bimestre - 2011
Matrizes
2º Bimestre - 2011
Binômio de Newton
- Representação algébrica de uma matriz;
- Tipos de matrizes;
- Diagonal principal e secundária;
- Igualdade de matrizes;
- Matriz transposta;
- Operações com matrizes;
- Matriz inversa;
Determinantes
-
- Fatorial;
- Números binômiais
- Triângulo de Pascal;
- Binômio de Newton;
- Números binomiais;
- Fórmula do termo geral;
Análise Combinatória
Cálculo do determinante de uma matriz quadrada;
cálculo do determinante de 3ª ordem;
Cálculo do determinante de ordem maior que três;
Propriedades;
Sistemas lineares
- Equação linear;
- Solução de uma equação linear;
- Sistemas de equações lineares;
- Sistema homogêneo;
- Matriz de um sistema;
- Sistema normal.
- Principio fundamental da contagem;
- Permutação simples;
- Arranjos simples;
- Combinações simples;
Probabilidades
- Experimentos aleatórios;
- Espaço amostral;
- Eventos;
- Eventos mutuamente exclusivos;
- Eventos complementares,
- Probabilidades
- Probabilidade da reunião de dois eventos;
Função Trigonométrica
- Arcos e ângulo, transformações de unidades trigonométricas;
- Razões Trigonométricas - seno, cosseno e tangente;
- Relação fundamental da Trigonometria;
- Variação, Gráficos e Conjunto Imagem das Funções Seno, Cosseno e Tangente;
3ª série
1º Bimestre - 2011
Geometria Espacial Métrica
-
- Raízes de uma equação polinomial;
- Equações polinomiais na forma fatorada;
- Número de raízes;
- Multiplicidade de uma raiz;
Noções de Estatística
Números imaginários;
Números complexos;
Igualdade;
Operações com números complexos;
Potências de i;
Forma Trigonométrica;
Polinômios
-
Equações Polinomiais
Poliedros;
Elementos do poliedro;
Nomenclatura dos poliedros;
Poliedros regulares;
Relação de Euler;
Prisma;
Pirâmide;
Cilindro circular;
Cone e esfera;
Números Complexos
-
2º Bimestre - 2011
- Freqüência, taxa percentual e gráfico de setores;
- gráfico em colunas ou em barras;
- Distribuição agrupada de freqüências;
- Polígonos de freqüências;
- Moda, média e mediana;
Noções de Matemática Financeira
Função polinomial;
Grau;
Valor Numérico;
Polinômios identicamente nulos;
polinômios idênticos;
Operações com polinômios;
Teorema do resto;
Dispositivo prático de Briot-Ruffini;
Observação:
A realização da recuperação de estudos é feita através da deliberação 007/99.
- Porcentagem;
- Juros
- Taxa de juros;
- Taxa unitária;
- Juros simples e compostos;