Combinatória 2 - Prof. Lúcio Fassarella

Problemas de Combinatória
Prof. Lúcio Fassarella
D M A /C EU N ES/U FES
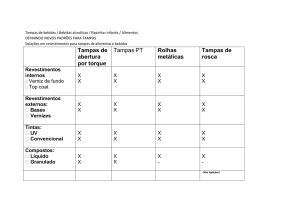
Problema 0.1 Os alunos de uma turma construiram caixas de madeira idênticas e decidiram pintá-las de branco, exceto as tampas quadradas. Para pintar as tampas, decidiram
riscar as duas diagonais de preto e pintar cada parte triangular de uma cor. No mínimo,
quantas cores eles precisam para pintar 25 tampas diferentes sem que dois triângulos adjacentes tenham a mesma cor?
Problema 0.2 Os alunos de uma turma construiram caixas de madeira circulares idênticas
e decidiram pintá-las de branco, exceto as tampas. Para pintar as tampas, decidiram dividilas em quatro setores congruentes e pintar cada um de uma cor. No mínimo, quantas cores
eles precisam para pintar 25 tampas diferentes sem que dois setores adjacentes tenham a
mesma cor?
Problema 0.3 Os alunos de uma turma construiram caixas de madeira circulares idênticas
e decidiram pintá-las de branco, exceto as tampas. Para pintar as tampas, decidiram dividilas em quatro setores congruentes e pintar cada um de uma cor. No mínimo, quantas cores
eles precisam para pintar 25 tampas diferentes?
Problema 0.4 Os alunos de uma turma construiram caixas de madeira circulares idênticas
e decidiram pintá-las de branco, exceto as tampas. Para pintar as tampas, decidiram dividilas em cinco setores congruentes e pintar cada um de uma cor. No mínimo, quantas cores
eles precisam para pintar 25 tampas diferentes sem que dois setores adjacentes tenham a
mesma cor?
Problema 0.5 Os alunos de uma turma construiram caixas de madeira idênticas e decidiram pintá-las de branco, exceto as tampas circulares. Para pintar as tampas, decidiram
dividi-las em setores congruentes e pintar cada setor de azul ou vermelho. No mínimo, quantos setores são necessários para pintar 25 tampas diferentes sem que dois setores adjacentes
tenham a mesma cor?
Problema 0.6 Os alunos de uma turma construiram caixas de madeira idênticas e decidiram pintá-las de branco, exceto as tampas circulares. Para pintar as tampas, decidiram
dividi-las em setores congruentes e pintar cada setor de azul, verde ou vermelho. No mínimo, quantos setores são necessários para pintar 50 tampas diferentes sem que dois setores
adjacentes tenham a mesma cor?
1
RESOLUÇÃO
Problema 0.1: Os alunos de uma turma construiram caixas de madeira idênticas e decidiram pintá-las de branco, exceto as tampas quadradas. Para pintar as tampas, decidiram
riscar as duas diagonais de preto e pintar cada parte triangular de uma cor. No mínimo,
quantas cores eles precisam para pintar 25 tampas diferentes sem que dois triângulos adjacentes tenham a mesma cor?
Resolução
Vamos dividir a resolução do problema em três etapas:
1. Primeiro, determinar quantas tampas com exatamente n cores se pode pintar nas
condições dadas, sendo n um número natural;
2. Depois, determinar quantas tampas com exatamente n cores se pode pintar nas condições
dadas tendo a disposição m cores para escolher, sendo n e m números naturais tais que
m n;
3. Finalmente, determinar quantas tampas se pode pintar nas condições dadas tendo a
disposição m cores para escolher, sendo m um número natural.
Para visualizar, cnsidere o seguinte desenho de uma tampa com seus triângulos nomeados
A, B, C, D:
1. Quantas tampas com exatamente n cores se pode pintar nas condições dadas?
(a) Caso n = 1: 0. Realmente, não é possível pintar nenhuma tampa usando somente
uma cor de modo a satisfazer a condição de que triângulos adjacentes tenham
cores distintas.
(b) Caso n = 2: 1. Com exatamente duas cores pode-se pintar as tampas de um único
modo: os triângulos A e D devem ser pintados da mesma cor e os triângulos C
e D devem ser pintados na outra cor; embora as cores possam ser trocadas, isso
não modi…ca a pintura da tampa devido à simetria de rotação por 90o .
2
(c) Caso n = 3: 3. Para determinar o número de tampas que podem ser pintadas
com exatamente 3 cores, observamos:
i) uma cor deve pintar dois triângulos não-adjacentes;
ii) cada uma das outras duas cores deve pintar um dos dois triângulos restantes.
Devido à simetria de rotação por 180o , a única escolha que deve ser feita é pela cor
que deve pintar dois triângulos não-adjacentes: concluimos que podemos pintar 3
tampas diferentes.
(d) Caso n = 4: 6. Começando pelo triângulo A, temos 4 possibilidades de cor para
pintá-lo, depois 3 possibilidades para o triângulo B, 2 possibilidades para o triângulo C e 1 possibilidade para o triângulo D; portanto, o número total de possibilidades é 24 = 4 3 2 1; entretanto, devido às simetrias de rotação por 90o ,
180o e 270o , esse número de possibilidades é o quádruplo do número de tampas
pintadas diferentes. Concluimos que podemos pintar 6 tampas diferentes.
(e) Caso n 5: 0. Realmente, não há como pintar 4 triângulos com 5 ou mais cores,
uma cor para cada triângulo.
2. Quantas tampas com exatamente n cores se pode pintar nas condições dadas tendo a
disposição m cores para escolher, sendo n e m números naturais tais que m n?
Denotando por Tn número de tampas que se ponde pintar com exatamente n cores, a
resposta para esta pergunta é
Cnm Tn ;
onde Cnm é o número de subconjuntos de n elementos que há num conjunto com m
elementos:
m!
:
Cnm =
n! (m n)!
n
3. Quantas tampas se pode pintar nas condições dadas tendo a disposição m cores para
escolher, sendo m um número natural?
Considerando os desenvolvimentos anteriores, a resposta é:
m
X
Ckm
Tk
k=1
onde T1 = 0, T2 = 1, T3 = 3, T4 = 6, Tk = 0 8k
m = 1 cor: C11
m = 2 cores: C12
m = 3 cores: C13
m = 4 cores:
m = 5 cores:
C15
C14
T1 +
T1 +
C25
5. Assim:
T1 = 0;
T1 + C22
T1 + C23
C24
T2 +
T2 +
C35
T2 = 1;
T2 + C33
T3 = 6;
C34
T3 + C44
T3 +
C45
T4 = 24;
T4 + C55
T5 = 70:
A resposta do problema é 5: com 5 cores dá para pintar 70 tampas diferentes (enquanto com 4 cores, dá para pintar apenas 24 tampas diferentes).
3
COMENTÁRIOS
Na aprendizagem e no ensino de técnicas de contagem, são importantes:
1. Organizar o raciocínio com base nos princípios fundamentais, sem depender de fórmulas.
2. Resolver problemas criativamente:
(a) desenhando;
(b) esquematizando;
(c) criando estratégias;
(d) usando materiais concretos.
3. Praticar e re‡etir: aprender com os erros.
4. Ler, escrever e interpretar problemas e soluções.
5. Ensinar mediante resolução de problemas:
(a) contextualizar;
(b) orientar e instigar;
(c) fomentar estratégias;
(d) evitar entregar a solução.
4