MAT-206 Parte II

MAT-206 Parte II
Walter T. Huaraca Vargas
11 de Maio de 2017
Números Complexos
Definição
Um número complexo é um par ordenado de número reais denotado por
z “ pa; bq, o conjunto de todos os números complexos serão:
C “ R ˆ R “ tpa; bq; a, b P Ru
Dado z “ pa; bq P C, o número a é chamado de parte real de z e b é
chamado de parte imaginaria de z e são denotados por a “ Repzq e
b “ Impzq respetivamente.
O plano Complexo
Um número complexo z é chamado de real se Impzq “ 0 e z é chamado de
imaginario puro se Repzq “ 0
Exemplo
Determinar analiticamente e geometricamente o conjunto de números
complexos tais que:
1
A “ tz P C; Repzq “ 5u
2
B “ tz P C; Impzq ď 4u
3
C “ tz P C; Repzq ` Impzq “ 3u
4
A “ tz P C; ´1 ď Repzq ď 1; ´1 ď Impzq ď 1u
Elementos Neutro e Oposto
z P C é o elemento neutro de C se, e somente se, Repzq “ Impzq “ 0. O
oposto do número complexo z “ pa; bq é o número complexo
´z “ ´pa; bq “ p´a; ´bq. Geometricamente.
Operações
Igualdade: Os números complexos pa; bq e pc; dq são iguais se, e
somente se, a “ c e b “ b.
Soma: A soma dos números complexos z1 “ pa1 ; b1 q e z2 “ pa2 ; b2 q
é o número complexo z “ z1 ` z2 “ pa1 ` a2 ; b1 ` b2 q.
Geometricamente.
Proposição
Se z1 ; z2 ; z3 P C, então:
S1: z1 ` z2 “ z2 ` z1
S2: pz1 ` z2 q ` z3 “ z1 ` pz2 ` z3 q
S3: Existe w P C; z ` w “ z para todo z P C
S4: Para todo z P C existe ´z P C tal que z ` p´zq “ p0; 0q
Operações
Produto: O produto dos números complexos z1 “ pa1 ; b1 q e
z2 “ pa2 ; b2 q é o número complexo
z “ z “ z1 ¨ z2 “ pa1 a2 ´ b1 b2 ; a1 b2 ` b1 a2 q.
Proposição
Se z1 ; z2 ; z3 P C e k P R então:
P1: z1 z2 “ z2 z1
P2: pz1 z2 qz3 “ z1 pz2 z3 q
P3: z1 pz2 ` z3 q “ z1 z2 ` z1 z3
P4: Existe w P C ‰ p0; 0q; zw “ z para todo z P C
P5: Para todo z P C, z ‰ p0; 0q existe z ˚ P C tal que zz ˚ “ p0; 0q
Observação
1
O elementos neutro aditivo e multiplicativo são únicos.
2
O elementos inverso aditivo e multiplicativo são únicos.
3
4
O número complexo p1; 0q é chamada unidade pode ser identificado
com 1 P R
O número complexo i “ p0; 1q é chamada unidade imaginaria, assim se
pa; b P Cq, então pa; bq “ pa; 0q ` p0; bq “ ap1; 0q ` bp0; 1q “ a ` ib
Teorema
Provar que i 2 “ ´1
Conjugação
Dado um número complexo z “ a ` ib o conjugado de z é o número
complexo denotado por z e definido por:
z “ a ´ ib
Geometricamente.
Proposição
C1 z1 ˘ z2 “ z1 ˘ z2
C2 z1 z2 “ z1 z2
C3 z “ z
C4 pzq´1 “ pz ´1 q sempre que z ‰ p0; 0q
C5 p zz12 q “
z1
z2
sempre que z2 ‰ p0; 0q
Módulo
Dado um número complexo z “ a ` ib, o módulo de z, denotado por }z} é
o número real definido por:
a
}z} “ a2 ` b 2
Geometricamente.
Propriedades
Sejam z; z1 ; z2 P C, então:
M1 Se z ‰ p0; 0q então }z} ą 0
M2 z “ p0; 0q se, e somente se }z} “ 0
M3 }z} “ } ´ z}
M4 }z}2 “ zz
M5 }z1 ` z2 } ď }z1 } ` }z2 }
M6 }z1 z2 } “ }z1 }}z2 }
M7 } zz12 } “
}z1 }
}z2 }
se z2 ‰ p0; 0q
M8 Repzq ď |Repzq| ď }z}, Impzq ď |Impzq| ď }z}
Exercicios
2
Se p1 ` 2iqx ` p3 ´ 5iqy “ 1 ´ 3i, calcular os valores de x e y .
?
?
Calcular i 3 , i 7 , i 8 , i 16 e i 17 Calcular p2 ` 3iqp5 ´ 6 3iq,
p2`iqp3´2iqp1`2iq 1`i
i
, i ` 1´i
p1´iq2
3
Provar que Repzq “
1
4
5
z`z
2 ,
Impzq “
z´z
2
Seja z um número complexo tal que }z} “ 1, calcular
}z ` 1}2 ` }1 ´ z}2
?
Calcular z 2 se z “ ´} ´ 1 ` i} ` 2i
Exercicios
1
Representar geometricamente as seguintes equações:
1
2
3
4
2
3
4
}z ´ i} “ 2
Rerzpz ` 2qs “ 3
}z} “ Repzq ` 1
}z ´ 1} ď 2}z ` 1}
z
w
Se z; w P C, provar que Rep z`w
q ` Rep z`w
q“1
Achar dois número complexos z1 e z2 tais que a soma seja o número
real a e a diferença o número imaginario puro ib.
?
Provar que |Repzq| ` |Impzq| ď 2}z}
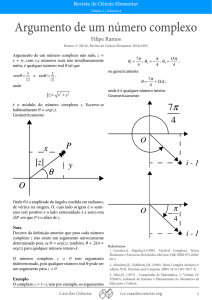
Forma Trigonométrica ou Polar
a
Dado o número complexo z “ x ` iy , z ‰ p0; 0q, seja r “ }x} “ x 2 ` y 2 ,
denotemos por θ o ângulo formado pelo segmento orientaso que representa
o número z com o eixo X em sentido antihorario. logo:
"
"
cospθq “ xr
x “ rcospθq
ñ
senpθq “ yr
y “ rsenpθq
De onde temos z “ x ` iy “ r pcospθq ` isenpθqq, chamado forma polar ou
trigonométrica do número complexo z, θ é chamado de argumento de z
Exercicios
1
Obter a forma polar dos seguintes números complexos:
§
§
§
§
z
z
z
z
?
“ 3`i?
“ ´2 ´ 2 3i
“ ´1 ´ i
“ ´4i
Expressar os números complexos na sua forma polar.
?
1 z “ 1 `
3i
?
2 z “ ´3 `
3i
Produto e Divisão em forma polar
Dados z1 “ r1 pcospθ1 q ` isenpθ1 qq; z2 “ r2 pcospθ2 q ` isenpθ2 qq P C então:
z1 z2 “ r1 r2 pcospθ1 ` θ2 q ` isenpθ1 ` θ2 qq
z1
r1
“ pcospθ1 ´ θ2 q ` isenpθ1 ´ θ2 qq
z2
r2
Exemplos
Calcular as potencias indicadas
1
2
3
p1 ´ iq5
?
p´1 ` 3iq7
?
p 3 ´ iq6
Potencia e raizes de números complexos
Teorema (Formula de Moivre)
Para todo z “ a ` ib P C e todo n P N temos:
pa “ ibqn “ r n pcospnθq ` isenpnθqq
Exemplo
Calcular p1 “
? 7
3iq
Teorema
Se z “ a ` bi é um número complexo e n P N. A raiz n-esima de z é
1
1
z n “ r n rcosp
Para k “ 0; 1; ¨ ¨ ¨ ; n ´ 1
Exemplo
1
Achar as raizes de p´4 ` 4iq 5
θ ` 2kπ
θ ` 2kπ
q ` isenp
qs
n
n
Exercicios
Efetuar as operações indicadas
? 1
1 p´128 ` 128
3iq 8
?
1
2 p4
3 ´ 4iq 3
n
3
nπ
Provar que p1 ` iqn “ 2 2 pCosp nπ
4 q ` iSenp 4 qq
4
Provar que se z `
5
1
z
“ 2cospθq então z m `
1
zm
“ 2cospmθq
usando a fórmula de Moivre provar Senp2xq “ 2SenpxqCospxq e
Cosp2xq “ Cos 2 pxq ´ Sen2 pxq
Exponenciais Complexos
Lembremos que se x P R a exponencial real é:
ex “ 1 ` x `
8
ÿ
x2
xk
` ¨¨¨ “
2!
k!
k“0
È facil observar que e 0 “ 1 e que e x`y “ e x e y . Se definirmos
e ix “ cospxq ` isenpxq, então poderemos definir:
e z “ e x pcospy q ` isenpy qq (Fórmular de Euler)
Proposição
E1 e z`w “ e z e w
E2 e z´w “
ez
ew
E3 e z “ 1 então z “ 2nπi, n P Z
E4 pe z qn “ e nz
Observação
1
cospxq “
2
senpxq “
3
e ix `e ´ix
2
e ix ´e ´ix
2
Se z “ a ` ib, então z “ re iθ , onde r “
de z.
?
a2 ` b 2 e θ é o argumento
Logaritmo em C
Observe que C “ tz “ re iθ ; r ě 0; 0 ď θ ă 2πu, assim neste contexto tem
inversa. Se z “ re iθ , existe um único w P C al que e w “ z, w é conhecido
como Lnpzq e é caraterizado por:
Lnpzq “ w “ Lnpr q ` ipθ ` 2kπq
Quando k “ 0, o logaritmo ? chamado de ramo principal ou valor principal
do logaritmo.
Exemplo
Achar Lnpzq onde z “ 1 ´ i