ExerciciosLançamento Horizontal e OblíquoXX

Lançamento Horizontal e Oblíquo
c) 5 2 m / s
d) 6 2 m / s
Parte I
e) 5 5 m / s
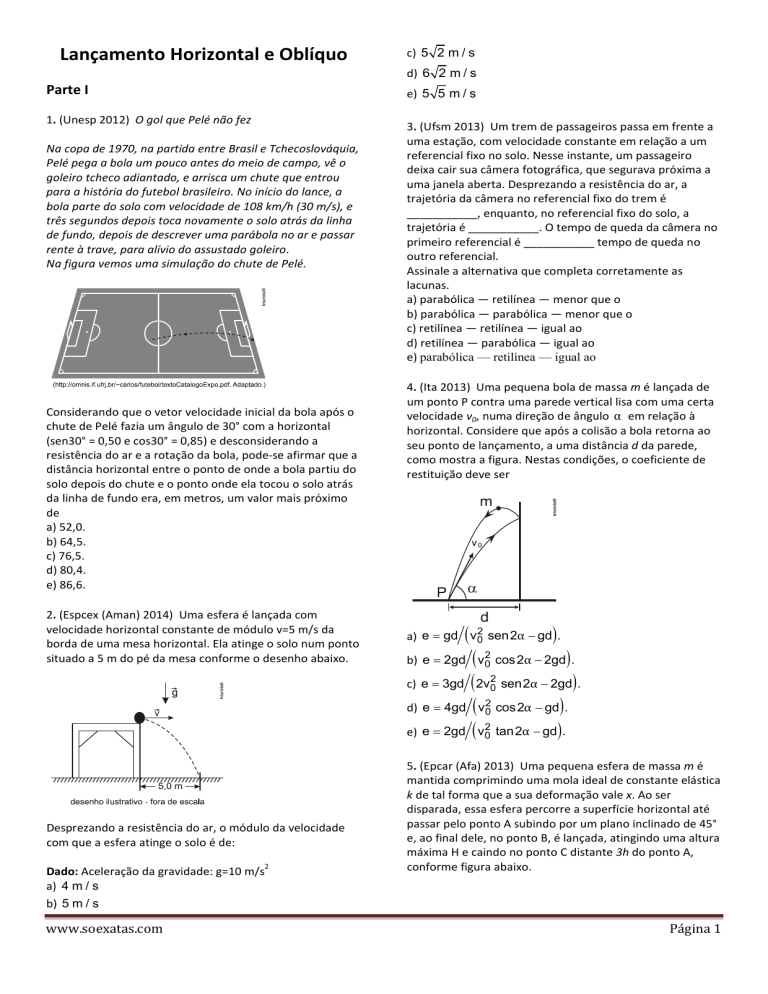
1. (Unesp 2012) O gol que Pelé não fez
Na copa de 1970, na partida entre Brasil e Tchecoslováquia,
Pelé pega a bola um pouco antes do meio de campo, vê o
goleiro tcheco adiantado, e arrisca um chute que entrou
para a história do futebol brasileiro. No início do lance, a
bola parte do solo com velocidade de 108 km/h (30 m/s), e
três segundos depois toca novamente o solo atrás da linha
de fundo, depois de descrever uma parábola no ar e passar
rente à trave, para alívio do assustado goleiro.
Na figura vemos uma simulação do chute de Pelé.
Considerando que o vetor velocidade inicial da bola após o
chute de Pelé fazia um ângulo de 30° com a horizontal
(sen30° = 0,50 e cos30° = 0,85) e desconsiderando a
resistência do ar e a rotação da bola, pode-se afirmar que a
distância horizontal entre o ponto de onde a bola partiu do
solo depois do chute e o ponto onde ela tocou o solo atrás
da linha de fundo era, em metros, um valor mais próximo
de
a) 52,0.
b) 64,5.
c) 76,5.
d) 80,4.
e) 86,6.
2. (Espcex (Aman) 2014) Uma esfera é lançada com
velocidade horizontal constante de módulo v=5 m/s da
borda de uma mesa horizontal. Ela atinge o solo num ponto
situado a 5 m do pé da mesa conforme o desenho abaixo.
Desprezando a resistência do ar, o módulo da velocidade
com que a esfera atinge o solo é de:
2
Dado: Aceleração da gravidade: g=10 m/s
a) 4 m / s
b) 5 m / s
www.soexatas.com
3. (Ufsm 2013) Um trem de passageiros passa em frente a
uma estação, com velocidade constante em relação a um
referencial fixo no solo. Nesse instante, um passageiro
deixa cair sua câmera fotográfica, que segurava próxima a
uma janela aberta. Desprezando a resistência do ar, a
trajetória da câmera no referencial fixo do trem é
___________, enquanto, no referencial fixo do solo, a
trajetória é ___________. O tempo de queda da câmera no
primeiro referencial é ___________ tempo de queda no
outro referencial.
Assinale a alternativa que completa corretamente as
lacunas.
a) parabólica — retilínea — menor que o
b) parabólica — parabólica — menor que o
c) retilínea — retilínea — igual ao
d) retilínea — parabólica — igual ao
e) parabólica — retilínea — igual ao
4. (Ita 2013) Uma pequena bola de massa m é lançada de
um ponto P contra uma parede vertical lisa com uma certa
velocidade v0, numa direção de ângulo α em relação à
horizontal. Considere que após a colisão a bola retorna ao
seu ponto de lançamento, a uma distância d da parede,
como mostra a figura. Nestas condições, o coeficiente de
restituição deve ser
(
)
a) e = gd v 02 sen2α − gd .
(
)
c) e = 3gd ( 2v02 sen2α − 2gd) .
d) e = 4gd ( v 02 cos 2α − gd) .
e) e = 2gd ( v 02 tan2α − gd) .
b) e = 2gd v 02 cos 2α − 2gd .
5. (Epcar (Afa) 2013) Uma pequena esfera de massa m é
mantida comprimindo uma mola ideal de constante elástica
k de tal forma que a sua deformação vale x. Ao ser
disparada, essa esfera percorre a superfície horizontal até
passar pelo ponto A subindo por um plano inclinado de 45°
e, ao final dele, no ponto B, é lançada, atingindo uma altura
máxima H e caindo no ponto C distante 3h do ponto A,
conforme figura abaixo.
Página 1
Considerando a aceleração da gravidade igual a g e
desprezando quaisquer formas de atrito, pode-se afirmar
que a deformação x é dada por
a) Dado que o arqueiro puxa as cordas por d = 30 cm,
calcule a velocidade de saída da flecha.
b) Calcule o intervalo de tempo necessário para que a
flecha caia no chão abaixo.
c) Calcule a distância horizontal D percorrida pela flecha até
tocar o chão.
1
 3 mgh  2
a) 

5 k 
b) 2
h2 k
mg
5
c) 
2
9. (Pucsp 2012) Dois amigos, Berstáquio e Protásio, distam
de 25,5 m. Berstáquio lança obliquamente uma bola para
Protásio que, partindo do repouso, desloca-se ao encontro
da bola para segurá-la. No instante do lançamento, a
direção da bola lançada por Berstáquio formava um ângulo
θ com a horizontal, o que permitiu que ela alcançasse, em
relação ao ponto de lançamento, a altura máxima de 11,25
m e uma velocidade de 8 m/s nessa posição. Desprezando o
2
atrito da bola com o ar e adotando g = 10m/s , podemos
afirmar que a aceleração de Protásio, suposta constante,
para que ele consiga pegar a bola no mesmo nível do
lançamento deve ser de
1
mgH  2
k
 H2k 
d)  3

 mg 


1
2
6. (Pucrj 2013) Um projétil é lançado com uma velocidade
escalar inicial de 20 m/s com uma inclinação de 30° com a
horizontal, estando inicialmente a uma altura de 5,0 m em
relação ao solo.
A altura máxima que o projétil atinge, em relação ao solo,
medida em metros, é:
2
Considere a aceleração da gravidade g = 10 m/s
a) 5,0
b) 10
c) 15
d) 20
e) 25
7. (G1 - cftmg 2013) Uma pedra ι lanηada para cima a partir
do topo e da borda de um edifνcio de 16,8 m de altura a uma
velocidade inicial v0 = 10 m/s e faz um βngulo de 53,1° com
a horizontal. A pedra sobe e em seguida desce em direηγo
ao solo. O tempo, em segundos, para que a mesma chegue
ao solo ι
a) 2,8.
b) 2,1.
c) 2,0.
d) 1,2.
8. (Pucrj 2012) Um arqueiro se prepara para lançar uma
flecha de massa 100 g da borda de um precipício, de altura
H = 320 m, utilizando uma balestra. O arqueiro retesa as
cordas da balestra, que podemos supor como sendo um
sistema de molas com um coeficiente k = 1440 N/m, para
lançar horizontalmente a flecha que segue a trajetória
representada na figura abaixo.
2
Dados: a resistência do ar é desprezível e g = 10 m/s
www.soexatas.com
a)
b)
c)
d)
e)
1
2
m/s
2
1
2
m/s
3
1
2
m/s
4
1
2
m/s
5
1
2
m/s
10
10. (Ucs 2012) Uma noiva, após a celebração do
casamento, tinha de jogar o buquê para as convidadas.
Como havia muitas ex-namoradas do noivo, ela fazia
questão de que sua melhor amiga o pegasse. Antes de se
virar para, de costas, fazer o arremesso do buquê, a noiva,
que possuía conhecimento sobre movimento balístico,
calculou a que distância aproximada a amiga estava dela:
5,7 m. Então ela jogou o buquê, tomando o cuidado para
que a direção de lançamento fizesse um ângulo de 60° com
Página 2
a horizontal. Se o tempo que o buquê levou para atingir a
altura máxima foi de 0,7 s, qual o valor aproximado da
velocidade dele ao sair da mão da noiva? (Despreze o atrito
com o ar. Considere a aceleração da gravidade igual a
1.
Trajetória da bola: quando se despreza a
resistência do ar, a trajetória da bola chutada, sob
2
a ação da gravidade (g = 10 m/s ), é dada por
2
h = d tgθ − 5 d² / v 02 (1 + tg θ ), em que v0 é a
(
10 m s2 , cos 60° = 0,5 e sen60° = 0,87.)
a) 1,5 m s
b) 5,5 m s
c) 6,0 m s
d) 8,0 m s
)
velocidade escalar inicial (em m/s), θ é o ângulo
de elevação (em radianos) e h é a altura (em m) da
bola a uma distância d (em m), do local do chute,
conforme figura abaixo.
e) 11,0 m s
11. (Unicamp 2012) Um jogador de futebol chuta uma bola
a 30 m do gol adversário. A bola descreve uma trajetória
parabólica, passa por cima da trave e cai a uma distância de
40 m de sua posição original. Se, ao cruzar a linha do gol, a
bola estava a 3 m do chão, a altura máxima por ela
alcançada esteve entre
2.
Débito cardíaco (DC): está relacionado ao volume
sistólico VS (volume de sangue bombeado a cada
batimento) e à frequência cardíaca FC pela
fórmula DC = VS x FC.
Utilize esses modelos para responder às seguintes
questões:
a) 4,1 e 4,4 m.
b) 3,8 e 4,1 m.
c) 3,2 e 3,5 m.
d) 3,5 e 3,8 m.
12. (Uem 2012) Do topo de uma plataforma vertical com
100 m de altura, é solto um corpo C1 e, no mesmo instante,
um corpo C2 é arremessado de um ponto na plataforma
situado a 80 m em relação ao solo, obliquamente formando
um ângulo de elevação de 30º com a horizontal e com
velocidade inicial de 20 m/s. Considerando que os corpos
estão, inicialmente, na mesma linha vertical, desprezando a
2
resistência do ar, e considerando g =10 m/s , assinale o que
for correto.
01) A altura máxima, em relação ao solo, atingida pelo
corpo C2 é de 85 m.
02) Os dois corpos atingem a mesma altura, em relação ao
solo, 1,5 segundos após o lançamento.
04) O corpo C2 demora mais de 6 segundos para atingir o
solo.
08) Os dois corpos atingem o solo no mesmo instante de
tempo.
16) A distância entre os corpos, 2 segundos após o
lançamento, é de 20 3 metros.
13. (Fuvest 2011) Os modelos permitem-nos fazer
previsões sobre situações reais, sendo, em geral,
simplificações, válidas em certas condições, de questões
complexas. Por exemplo, num jogo de futebol, a trajetória
da bola, após o chute, e o débito cardíaco dos jogadores
podem ser descritos por modelos.
www.soexatas.com
a) Durante uma partida, um jogador de futebol quer fazer
um passe para um companheiro a 32 m de distância. Seu
chute produz uma velocidade inicial na bola de 72 km/h.
Calcule os valores de tg θ necessários para que o passe
caia exatamente nos pés do companheiro.
b) Dois jogadores, A e B, correndo moderadamente pelo
campo, têm frequência cardíaca de 120 batimentos por
minuto. O jogador A tem o volume sistólico igual a 4/5
do volume sistólico do jogador B. Os dois passam a
correr mais rapidamente. A frequência cardíaca do
jogador B eleva-se para 150 batimentos por minuto. Para
quanto subirá a frequência cardíaca do jogador A se a
variação no débito cardíaco (DCfinal – DCinicial) de ambos
for a mesma?
14. (Ufu 2011) Uma pedra é lançada do solo com
velocidade de 36 km/h fazendo um ângulo de 45° com a
2
horizontal. Considerando g = 10 m/s e desprezando a
resistência do ar, analise as afirmações abaixo.
I. A pedra atinge a altura máxima de 2,5 m.
II. A pedra retorna ao solo ao percorrer a distância de 10 m
na horizontal.
III. No ponto mais alto da trajetória, a componente
horizontal da velocidade é nula.
Usando as informações do enunciado, assinale a alternativa
correta.
a) Apenas I é verdadeira.
b) Apenas I e II são verdadeiras.
c) Apenas II e III são verdadeiras.
d) Apenas II é verdadeira.
Página 3
15. (Ufpr 2011) Na cobrança de uma falta durante uma
partida de futebol, a bola, antes do chute, está a uma
distância horizontal de 27 m da linha do gol. Após o chute,
ao cruzar a linha do gol, a bola passou a uma altura de 1,35
m do chão quando estava em movimento descendente, e
levou 0,9 s neste movimento. Despreze a resistência do ar e
2
considere g = 10 m/s .
a) Calcule o módulo da velocidade na direção vertical no
instante em que a bola foi chutada.
b) Calcule o ângulo, em relação ao chão, da força que o
jogador imprimiu sobre a bola pelo seu chute.
c) Calcule a altura máxima atingida pela bola em relação ao
solo.
02) As componentes do vetor posição do projétil, em
qualquer instante, são dadas por,
1 2
x = V0 . cos θ . t e y = V0 . sen θ - gt
2
04) O alcance do projétil na direção horizontal depende da
velocidade e do ângulo de lançamento.
08) O tempo que o projétil permanece no ar é
V .senθ
t=2 0
g
16) O projétil executa simultaneamente um movimento
variado na direção vertical e um movimento uniforme
na direção horizontal.
16. (G1 - cftmg 2011) Um garoto gira uma pedra presa a
extremidade de um barbante de 1,0 m de comprimento,
em movimento circular uniforme, no plano vertical, com
uma frequência de 60 Hz. Ele solta o barbante no momento
em que a velocidade da pedra forma um angulo de 37° com
a horizontal, como mostra a figura.
18. (Uff 2011) Após um ataque frustrado do time
adversário, o goleiro se prepara para lançar a bola e armar
um contra-ataque.
Para dificultar a recuperação da defesa adversária, a bola
deve chegar aos pés de um atacante no menor tempo
possível. O goleiro vai chutar a bola, imprimindo sempre a
mesma velocidade, e deve controlar apenas o ângulo de
lançamento. A figura mostra as duas trajetórias possíveis da
bola num certo momento da partida.
Desprezando-se qualquer forma de atrito, o alcance
horizontal, atingido pela pedra em relação a posição de
lançamento, vale, aproximadamente, em metros,
a) 349π
2
b) 742π
c) 968π
2
2
d) 1382π
2
17. (Uepg 2011) Um projétil quando é lançado
obliquamente, no vácuo, ele descreve uma trajetória
parabólica. Essa trajetória é resultante de uma composição
de dois movimentos independentes. Analisando a figura
abaixo, que representa o movimento de um projétil
lançado obliquamente, assinale o que for correto.
Assinale a alternativa que expressa se é possível ou não
determinar qual destes dois jogadores receberia a bola no
menor tempo. Despreze o efeito da resistência do ar.
a) Sim, é possível, e o jogador mais próximo receberia a
bola no menor tempo.
b) Sim, é possível, e o jogador mais distante receberia a
bola no menor tempo.
c) Os dois jogadores receberiam a bola em tempos iguais.
d) Não, pois é necessário conhecer os valores da velocidade
inicial e dos ângulos de lançamento.
e) Não, pois é necessário conhecer o valor da velocidade
inicial.
19. (Unesp 2006) Uma esfera maciça A encontra-se em
repouso na borda de uma mesa horizontal, a uma altura h
de 0,45m do solo. Uma esfera B, também maciça, desliza
com uma velocidade de 4,0 m/s sobre a mesa e colide
frontalmente com a esfera A, lançando-a ao solo, conforme
ilustra a figura.
01) As componentes da velocidade do projétil, em qualquer
instante nas direções x e y, são respectivamente dadas por,
Vx = V0 . cos θ e Vy = V0 . sen θ – gt
Sendo uma colisão inelástica, a esfera B retorna na mesma
www.soexatas.com
Página 4
direção de incidência com velocidade de 2,0 m/s em
módulo e a esfera A toca o solo a uma distância 2h da
borda da mesa.
2
Considerando g = 10 m/s , calcule
a) a velocidade com que A foi lançada ao solo.
b) a razão mA/mB.
20. (Ita 2006) Animado com velocidade inicial, v0, o objeto
X, de massa m, desliza sobre um piso horizontal ao longo de
uma distância d, ao fim da qual colide com o objeto Y, de
mesma massa, que se encontra inicialmente parado na
beira de uma escada de altura h. Com o choque, o objeto Y
atinge o solo no ponto P. Chamando μ(k) o coeficiente de
atrito cinético entre o objeto X e o piso, g a aceleração da
gravidade e desprezando a resistência do ar, assinale a
expressão que dá a distância d.
a) d =
1  2 s2 g 
 v0 −

2μk g 
2h 
b) d =
−1  2 s2 g 
 v0 −

2μk g 
2h 
−v 0 
g 
 v 0 − s

2μ k g 
2h 
1  2 s2 g 
d) d =
 2v 0 −

2μk g 
2h 
c) d =
e) d =
−v 0 
g 
 v 0 − s

μk g 
2h 
21. (Ufmg 2006) Clarissa chuta, em sequência, três bolas P, Q e R -, cujas trajetórias estão representadas nesta
figura:
Sejam t(P), t(Q) e t(R) os tempos gastos, respectivamente,
pelas bolas P, Q e R, desde o momento do chute até o
instante em que atingem o solo.
Considerando-se essas informações, é CORRETO afirmar
que
a) t(Q) > t(P) = t(R)
b) t(R) > t(Q) = t(P)
c) t(Q) > t(R) > t(P)
d) t(R) > t(Q) > t(P)
22. (Ufjf 2006) Durante uma partida de futebol, um
jogador, percebendo que o goleiro do time adversário está
longe do gol, resolve tentar um chute de longa distância
(vide figura). O jogador se encontra a 40 m do goleiro. O
vetor velocidade inicial da bola tem módulo v0 = 26 m/s e
°
faz um ângulo de 25 com a horizontal, como mostra a
figura a seguir.
Desprezando a resistência do ar, considerando a bola
°
°
pontual e usando cos 25 = 0,91 e sen 25 = 0,42:
a) Faça o diagrama de forças sobre a bola num ponto
qualquer da trajetória durante o seu voo, após ter sido
chutada. Identifique a(s) força(s).
b) Saltando com os braços esticados, o goleiro pode atingir
a altura de 3,0 m. Ele consegue tocar a bola quando ela
passa sobre ele? Justifique.
c) Se a bola passar pelo goleiro, ela atravessará a linha de
gol a uma altura de 1,5 m do chão. A que distância o
jogador se encontrava da linha de gol, quando chutou a
bola? (Nota: a linha de gol está atrás do goleiro.)
23. (G1 - cftce 2006) Um aluno do CEFET em uma partida
de futebol lança uma bola para cima, numa direção que
°
forma um ângulo de 60 com a horizontal. Sabendo que a
velocidade na altura máxima é 20 m/s, podemos afirmar
que a velocidade de lançamento da bola, em m/s, será:
a) 10
b) 17
c) 20
d) 30
e) 40
24. (Ufg 2006) Os quatro blocos, representados na figura
com suas respectivas massas, são abandonados em um
plano inclinado que não apresenta atrito e termina voltado
para a direção horizontal.
www.soexatas.com
Página 5
Os blocos, ao deixarem a plataforma, descrevem trajetórias
parabólicas em queda livre e alcançam o solo, formando, da
esquerda para a direita, a sequência:
a) m; 5m; 2m; 3m
b) m; 2m; 3m; 5m
c) 3m; 2m; 5m; m
d) 3m; 5m; m; 2m
e) 5m; 3m; 2m; m
25. (Uel 1996) Um projétil é atirado com velocidade de 40
°
m/s, fazendo ângulo de 37 com a horizontal. A 64 m do
ponto de disparo, há um obstáculo de altura 20 m.
2
°
°
Adotando g = 10 m/s , cos 37 = 0,80 e sen 37 = 0,60, podese concluir que o projétil
a) passa à distância de 2,0 m acima do obstáculo.
b) passa à distância de 8,0 m acima do obstáculo.
c) choca-se com o obstáculo a 12 m de altura.
d) choca-se com o obstáculo a 18 m de altura.
e) cai no solo antes de chegar até o obstáculo.
26. (Fuvest 1990) Num dia ensolarado, com sol a pique, um
jogador chuta uma bola, que descreve no ar uma parábola.
O gráfico que melhor representa o valor da velocidade v da
sombra da bola, projetada no solo, em função do tempo t,
é:
Nas condições descritas do movimento parabólico da bola,
considerando a aceleração da gravidade no local igual a 10
2
m/s , 2 igual a 1,4 e desprezando-se as perdas de
energia mecânica durante o voo da bola, determine,
aproximadamente:
a) o módulo da velocidade de lançamento da bola, em m/s.
b) a altura máxima, em metros, atingida pela bola.
2. (Unifesp 2010) No campeonato paulista de
futebol, um famoso jogador nos presenteou com um lindo
gol, no qual, ao correr para receber um lançamento de um
dos atacantes, o goleador fenomenal parou a bola no peito
do pé e a chutou certeira ao gol. Analisando a jogada pela
TV, verifica-se que a bola é chutada pelo armador da jogada
a partir do chão com uma velocidade inicial de 20,0 m/s,
fazendo um ângulo com a horizontal de 45º para cima.
2
Dados: g = 10,0 m/s e
2 = 1,4
a) Determine a distância horizontal percorrida pela bola
entre o seu lançamento até a posição de recebimento
pelo artilheiro (goleador fenomenal).
b) No instante do lançamento da bola, o artilheiro estava a
16,0 m de distância da posição em que ele estimou que a
bola cairia e, ao perceber o início da jogada, corre para
receber a bola. A direção do movimento do artilheiro é
perpendicular à trajetória da bola, como mostra a figura.
Qual é a velocidade média, em km/h, do artilheiro, para
que ele alcance a bola imediatamente antes de ela tocar
o gramado?
Parte II
1. (Unifesp 2013) O atleta húngaro Krisztian Pars
conquistou medalha de ouro na olimpíada de Londres no
lançamento de martelo. Após girar sobre si próprio, o atleta
lança a bola a 0,50m acima do solo, com velocidade linear
inicial que forma um ângulo de 45° com a horizontal. A bola
toca o solo após percorrer a distância horizontal de 80m.
www.soexatas.com
3. (Unifesp 2006) Um projétil de massa m = 0,10 kg é
lançado do solo com velocidade de 100 m/s, em um
°
instante t = 0, em uma direção que forma 53 com a
horizontal. Admita que a resistência do ar seja desprezível e
2
adote g = 10 m/s .
a) Utilizando um referencial cartesiano com a origem
localizada no ponto de lançamento, qual a abscissa x e a
ordenada y da posição desse projétil no instante t = 12
Página 6
s?
°
°
Dados: sen 53 = 0,80; cos 53 = 0,60.
b) Utilizando este pequeno trecho da trajetória do projétil:
Desenhe no ponto O, onde está representada a velocidade
1. (Unesp 2012) O gol que Pelé não fez
Na copa de 1970, na partida entre Brasil e Tchecoslováquia,
Pelé pega a bola um pouco antes do meio de campo, vê o
goleiro tcheco adiantado, e arrisca um chute que entrou
para a história do futebol brasileiro. No início do lance, a
bola parte do solo com velocidade de 108 km/h (30 m/s), e
três segundos depois toca novamente o solo atrás da linha
de fundo, depois de descrever uma parábola no ar e passar
rente à trave, para alívio do assustado goleiro.
Na figura vemos uma simulação do chute de Pelé.
v do projétil, a força resultante F que nele atua. Qual o
módulo dessa força?
4. (Unifesp 2004) Uma pequena esfera maciça é lançada de
uma altura de 0,6 m na direção horizontal, com velocidade
inicial de 2,0 m/s. Ao chegar ao chão, somente pela ação da
gravidade, colide elasticamente com o piso e é lançada
2
novamente para o alto. Considerando g = 10,0 m/s , o
módulo da velocidade e o ângulo de lançamento do solo,
em relação à direção horizontal, imediatamente após a
colisão, são respectivamente dados por
°
a) 4,0 m/s e 30 .
°
b) 3,0 m/s e 30 .
°
c) 4,0 m/s e 60 .
°
d) 6,0 m/s e 45 .
°
e) 6,0 m/s e 60 .
5. (Unifesp 2003) Em um acidente de trânsito, uma
testemunha deu o seguinte depoimento:
"A moto vinha em alta velocidade, mas o semáforo estava
vermelho para ela. O carro que vinha pela rua transversal
parou quando viu a moto, mas já era tarde; a moto bateu
violentamente na lateral do carro. A traseira da moto
levantou e seu piloto foi lançado por cima do carro".
A perícia supôs, pelas características do choque, que o
motociclista foi lançado horizontalmente de uma altura de
1,25 m e caiu no solo a 5,0 m do ponto de lançamento,
medidos na horizontal. As marcas de pneu no asfalto plano
e horizontal mostraram que o motociclista acionou
bruscamente os freios da moto, travando as rodas, 12,5 m
antes da batida. Após análise das informações coletadas, a
perícia concluiu que a moto deveria ter atingido o carro a
uma velocidade de 54 km/h (15 m/s).
2
Considerando g = 10 m/s e o coeficiente de atrito entre o
asfalto e os pneus 0,7, determine:
a) a velocidade de lançamento do motociclista, em m/s;
b) a velocidade da moto antes de começar a frear.
Considerando que o vetor velocidade inicial da bola após o
chute de Pelé fazia um ângulo de 30° com a horizontal
(sen30° = 0,50 e cos30° = 0,85) e desconsiderando a
resistência do ar e a rotação da bola, pode-se afirmar que a
distância horizontal entre o ponto de onde a bola partiu do
solo depois do chute e o ponto onde ela tocou o solo atrás
da linha de fundo era, em metros, um valor mais próximo
de
a) 52,0.
b) 64,5.
c) 76,5.
d) 80,4.
e) 86,6.
2. (Unesp 2007) Em uma partida de futebol, a bola é
chutada a partir do solo descrevendo uma trajetória
parabólica cuja altura máxima e o alcance atingido são,
respectivamente, h e s. Desprezando o efeito do atrito do
ar, a rotação da bola e sabendo que o ângulo de
°
lançamento foi de 45 em relação ao solo horizontal, calcule
a razão s/h.
°
°
Dado: sen 45 = cos 45 =
2
.
2
3. (Unesp 2006) Uma esfera maciça A encontra-se em
repouso na borda de uma mesa horizontal, a uma altura h
de 0,45m do solo. Uma esfera B, também maciça, desliza
com uma velocidade de 4,0 m/s sobre a mesa e colide
frontalmente com a esfera A, lançando-a ao solo, conforme
ilustra a figura.
Parte III
www.soexatas.com
Página 7
comparado à altura do muro e que durante a trajetória não
houve movimento de rotação ou perda de energia.
2
Tomando g = 10 m/s , calcule
a) o tempo decorrido, desde o lançamento, para a mochila
atingir a altura máxima.
b) o ângulo de lançamento.
Dados:
Sendo uma colisão inelástica, a esfera B retorna na mesma
direção de incidência com velocidade de 2,0 m/s em
módulo e a esfera A toca o solo a uma distância 2h da
borda da mesa.
2
Considerando g = 10 m/s , calcule
a) a velocidade com que A foi lançada ao solo.
b) a razão mA/mB.
4. (Unesp 2006) Para determinar a velocidade de um
projétil, um perito, devidamente autorizado, toma um
pequeno bloco de madeira, com massa de 480 g e o coloca
em repouso na borda de um balcão horizontal de altura h =
1,25 m. A seguir, dispara o projétil, de massa 20 g,
paralelamente ao balcão. O projétil penetra no bloco,
lançando-o
o ao solo, a uma distância d = 5,0 m da borda do
balcão, como ilustrado na figura.
2
Considerando g = 10 m/s e desprezando os efeitos de
atrito com o ar e o movimento de rotação do projétil e do
bloco, calcule
a) a velocidade com que o bloco deixa o balcão.
b) a velocidade do projétil obtida pelo perito.
5. (Unesp 2006) Um garoto, voltando da escola, encontrou
seus amigos jogando uma partida de futebol no campinho
ao lado de sua casa e resolveu participar da brincadeira.
Para não perder tempo, atirou sua mochila por cima do
muro, para o quintal de sua casa: postou-se
se a uma
um distância
de 3,6 m do muro e, pegando a mochila pelas alças, lançoulançou
a a partir de uma altura de 0,4 m. Para que a mochila
passasse para o outro lado com segurança, foi necessário
que o ponto mais alto da trajetória estivesse a 2,2 m do
solo. Considere quee a mochila tivesse tamanho desprezível
www.soexatas.com
6. (Unesp 2003) Um motociclista deseja saltar um fosso de
largura d=4,0m, que separa duas plataformas horizontais.
As plataformas estão em níveis diferentes, sendo que a
primeira encontra-se
se a uma altura h=1,25m acima
ac
do nível
da segunda, como mostra a figura.
O motociclista salta o vão com certa velocidade u0 e alcança
a plataforma inferior, tocando-a
tocando com as duas rodas da
motocicleta ao mesmo tempo. Sabendo-se
Sabendo que a distância
2
entre os eixos das rodas é 1,0m e admitindo g=10 m/s ,
determine:
a) o tempo gasto entre os instantes em que ele deixa a
plataforma superior
erior e atinge a inferior.
b) qual é a menor velocidade com que o motociclista deve
deixar a plataforma superior, para que não caia no fosso.
7. (Unesp 1999) A figura mostra duas esferas, 1 e 2, de
massas m1 e m2, respectivamente, comprimindo uma mola
e mantidas por duas travas dentro de um tubo horizontal.
Página 8
é 3,0 m/s. Supondo que o corpo esteja sujeito
exclusivamente à ação da gravidade, determine sua energia
cinética:
a) no instante do lançamento;
b) no ponto mais alto da trajetória.
10. (Unesp 1993) Uma pequena esfera é lançada
horizontalmente do alto de um edifício com velocidade v0 .
Quando as travas são retiradas simultaneamente, as
esferas 1 e 2 são ejetadas do tubo, com velocidades v1 e v2,
respectivamente, e caem sob ação da gravidade. A esfera 1
atinge o solo num ponto situado à distância x1 = 0,50 m, t1
segundos depois de abandonar o tubo, e a esfera 2 à
distância x2 = 0,75 m, t2 segundos depois de abandonar o
tubo, conforme indicado na figura.
Desprezando a massa de mola e quaisquer atritos,
determine
a) as razões t2/t1 e v2/v1.
b) a razão m2/m1.
A figura a seguir mostra a velocidade v da esfera no ponto
P da trajetória, t segundos após o lançamento, e a escala
utilizada para representar esse vetor (as linhas verticais do
quadriculado são paralelas à direção do vetor aceleração da
gravidade g).
2
8. (Unesp 1997) Duas pequenas esferas idênticas, 1 e 2,
são lançadas do parapeito de uma janela,
perpendicularmente à parede, com velocidades horizontais
Considerando g = 10m/s e desprezando a resistência
oferecida pelo ar, determine, a partir da figura:
V1 e V 2 , com V2 > V1, como mostra a figura, e caem sob a
b) o instante t em que a esfera passa pelo ponto P.
a) o módulo de v0 ;
ação da gravidade.
Parte IV
1. (Uerj 2013) Três blocos de mesmo volume, mas de
materiais e de massas diferentes, são lançados
obliquamente para o alto, de um mesmo ponto do solo, na
mesma direção e sentido e com a mesma velocidade.
Observe as informações da tabela:
A esfera 1 atinge o solo num ponto situado à distância x1 da
parede, t1 segundos depois de abandonar o parapeito, e a
esfera 2 num ponto situado à distância x2 da parede, t2
segundos depois de abandonar o parapeito. Desprezando a
resistência oferecida pelo ar e considerando o solo plano e
horizontal, podemos afirmar que
a) x1 = x2 e t1 = t2.
b) x1 < x2 e t1 < t 2.
c) x1 = x2 e t1 > t2.
d) x1 > x2 e t1 < t2.
e) x1 < x2 e t1 = t2.
9. (Unesp 1997) Um corpo de massa 1,0 kg é lançado
obliquamente, a partir do solo, sem girar. O valor da
componente vertical da velocidade, no instante do
lançamento, é 2,0 m/s e o valor da componente horizontal
www.soexatas.com
Material do bloco
chumbo
ferro
granito
Alcance do lançamento
A1
A2
A3
A relação entre os alcances A1, A2 e A3 está apresentada
em:
a) A1 > A2 > A3
b) A1 < A2 < A3
c) A1 = A2 > A3
d) A1 = A2 = A3
TEXTO PARA A PRÓXIMA QUESTÃO:
Três bolas − X, Y e Z − são lançadas da borda de uma mesa,
com velocidades iniciais paralelas ao solo e mesma direção
e sentido. A tabela abaixo mostra as magnitudes das
massas e das velocidades iniciais das bolas.
Página 9
Bolas
X
Y
Z
Massa
(g)
5
5
10
Velocidade inicial
(m/s)
20
10
8
1. (Fuvest 2011) Os modelos permitem-nos fazer previsões
sobre situações reais, sendo, em geral, simplificações,
válidas em certas condições, de questões complexas. Por
exemplo, num jogo de futebol, a trajetória da bola, após o
chute, e o débito cardíaco dos jogadores podem ser
descritos por modelos.
1.
Trajetória da bola: quando se despreza a
resistência do ar, a trajetória da bola chutada, sob
2
a ação da gravidade (g = 10 m/s ), é dada por
2
h = d tgθ − 5 d² / v 02 (1 + tg θ ), em que v0 é a
2. (Uerj 2012) As relações entre os respectivos tempos de
queda t x , t y e t z das bolas X, Y e Z estão apresentadas
(
em:
a) t x < t y < t z
b) t y < t z < t x
)
velocidade escalar inicial (em m/s), θ é o ângulo
de elevação (em radianos) e h é a altura (em m) da
bola a uma distância d (em m), do local do chute,
conforme figura abaixo.
c) t z < t y < t x
d) t y = t x = t z
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Um trem em alta velocidade desloca-se ao longo
de um trecho retilíneo a uma velocidade constante de 108
km/h. Um passageiro em repouso arremessa
horizontalmente ao piso do vagão, de uma altura de 1 m,
na mesma direção e sentido do deslocamento do trem,
uma bola de borracha que atinge esse piso a uma distância
de 5 m do ponto de arremesso.
3. (Uerj 2011) O intervalo de tempo, em segundos, que a
bola leva para atingir o piso é cerca de:
a) 0,05
b) 0,20
c) 0,45
d) 1,00
4. (Uerj 2011) Se a bola fosse arremessada na mesma
direção, mas em sentido oposto ao do deslocamento do
trem, a distância, em metros, entre o ponto em que a bola
atinge o piso e o ponto de arremesso seria igual a:
a) 0
b) 5
c) 10
d) 15
5. (Uerj 2009) Um avião, em trajetória retilínea paralela à
superfície horizontal do solo, sobrevoa uma região com
velocidade constante igual a 360 km/h.
Três pequenas caixas são largadas, com velocidade inicial
nula, de um compartimento na base do avião, uma a uma, a
intervalos regulares iguais a 1 segundo.
Desprezando-se os efeitos do ar no movimento de queda
das caixas, determine as distâncias entre os respectivos
pontos de impacto das caixas no solo.
Parte V
www.soexatas.com
2.
Débito cardíaco (DC): está relacionado ao volume
sistólico VS (volume de sangue bombeado a cada
batimento) e à frequência cardíaca FC pela
fórmula DC = VS x FC.
Utilize esses modelos para responder às seguintes
questões:
a) Durante uma partida, um jogador de futebol quer fazer
um passe para um companheiro a 32 m de distância. Seu
chute produz uma velocidade inicial na bola de 72 km/h.
Calcule os valores de tg θ necessários para que o passe
caia exatamente nos pés do companheiro.
b) Dois jogadores, A e B, correndo moderadamente pelo
campo, têm frequência cardíaca de 120 batimentos por
minuto. O jogador A tem o volume sistólico igual a 4/5
do volume sistólico do jogador B. Os dois passam a
correr mais rapidamente. A frequência cardíaca do
jogador B eleva-se para 150 batimentos por minuto. Para
quanto subirá a frequência cardíaca do jogador A se a
variação no débito cardíaco (DCfinal – DCinicial) de ambos
for a mesma?
2. (Fuvest 2009) O salto que conferiu a medalha de ouro a
uma atleta brasileira, na Olimpíada de 2008, está
representado no esquema ao lado, reconstruído a partir de
fotografias múltiplas. Nessa representação, está indicada,
também, em linha tracejada, a trajetória do centro de
massa da atleta (CM).
Utilizando a escala estabelecida pelo comprimento do salto,
de 7,04 m, é possível estimar que o centro de massa da
atleta atingiu uma altura máxima de 1,25 m (acima de sua
Página 10
altura inicial), e que isso ocorreu a uma distância de 3,0 m,
na horizontal, a partir do início do salto, como indicado na
figura. Considerando essas informações, estime:
Parte VI
1. (Unicamp 2012) Um jogador de futebol chuta uma bola a
30 m do gol adversário. A bola descreve uma trajetória
parabólica, passa por cima da trave e cai a uma distância de
40 m de sua posição original. Se, ao cruzar a linha do gol, a
bola estava a 3 m do chão, a altura máxima por ela
alcançada esteve entre
Desconsidere os efeitos da resistência do ar.
a) O intervalo de tempo t1, em s, entre o instante do início
do salto e o instante em que o centro de massa da atleta
atingiu sua altura máxima.
b) A velocidade horizontal média, VH, em m/s,
/s, da atleta
durante o salto.
c) O intervalo de tempo t2, em s, entre o instante em que a
atleta atingiu sua altura máxima e o instante final do salto.
NOTE E ADOTE: Desconsidere os efeitos da resistência do
ar.
3. (Fuvest 2008) No "salto com vara", um atleta corre
segurando uma vara e, com perícia e treino, consegue
projetar seu corpo por cima de uma barra. Para uma
estimativa da altura alcançada nesses saltos, é possível
considerar que a vara sirva apenas para converter o
movimento horizontal do atleta
leta (corrida) em movimento
vertical, sem perdas ou acréscimos de energia. Na análise
de um desses saltos, foi obtida a sequência de imagens
reproduzida a seguir. Nesse caso, é possível estimar que a
velocidade máxima atingida pelo atleta, antes do salto, foi
de, aproximadamente,
Desconsidere os efeitos do trabalho muscular após o início
do salto.
a) 4 m/s
b) 6 m/s
c) 7 m/s
d) 8 m/s
e) 9 m/s
www.soexatas.com
a) 4,1 e 4,4 m.
b) 3,8 e 4,1 m.
c) 3,2 e 3,5 m.
d) 3,5 e 3,8 m.
2. (Unicamp 2005) O famoso salto duplo twistcarpado de
Daiane dos Santos foi analisado durante um dia de
treinamento no Centro Olímpico em Curitiba, através de
sensores e filmagens que permitiram reproduzir a trajetória
do centro de gravidade de Daiane na direção vertical (em
metros), assim como o tempo de duração do salto.
De acordo com o gráfico, determine:
a) A altura
tura máxima atingida pelo centro de gravidade de
Daiane.
b) A velocidade média horizontal do salto, sabendo-se
sabendo que
a distância percorrida nessa direção é de 1,3m.
c) A velocidade vertical de saída do solo.
3. (Unicamp 2004) Uma bola de tênis rebatida numa das
extremidades da quadra descreve a trajetória representada
na figura a seguir, atingindo o chão na outra extremidade
da quadra. O comprimento da quadra é de 24 m.
Página 11
a) Calcule o tempo de voo da bola, antes de atingir o chão.
Desconsidere a resistência do ar nesse caso.
b) Qual é a velocidade horizontal da bola no caso acima?
c) Quando a bola é rebatida com efeito, aparece uma força,
FE, vertical, de cima para baixo e igual a 3 vezes o peso da
bola. Qual será a velocidade horizontal da bola, rebatida
com efeito para uma trajetória idêntica à da figura?
4. (Unicamp 2002) Até os experimentos de Galileu Galilei,
pensava-se que quando um projétil era arremessado, o seu
movimento devia-se ao impetus, o qual mantinha o projétil
em linha reta e com velocidade constante. Quando o
impetus acabasse, o projétil cairia verticalmente até atingir
o chão. Galileu demonstrou que a noção de impetus era
equivocada. Consideremos que um canhão dispara
projéteis com uma velocidade inicial de 100m/s, fazendo
°
um ângulo de 30 com a horizontal. Dois artilheiros
calcularam a trajetória de um projétil: um deles, Simplício,
utilizou a noção de impetus, o outro, Salviati, as ideias de
Galileu. Os dois artilheiros concordavam apenas em uma
coisa: o alcance do projétil. Considere
o atrito com o ar.
3 ≈ 1,8. Despreze
a) Qual o alcance do projétil?
b) Qual a altura máxima alcançada pelo projétil, segundo os
cálculos de Salviati?
c) Qual a altura máxima calculada por Simplício?
www.soexatas.com
Página 12