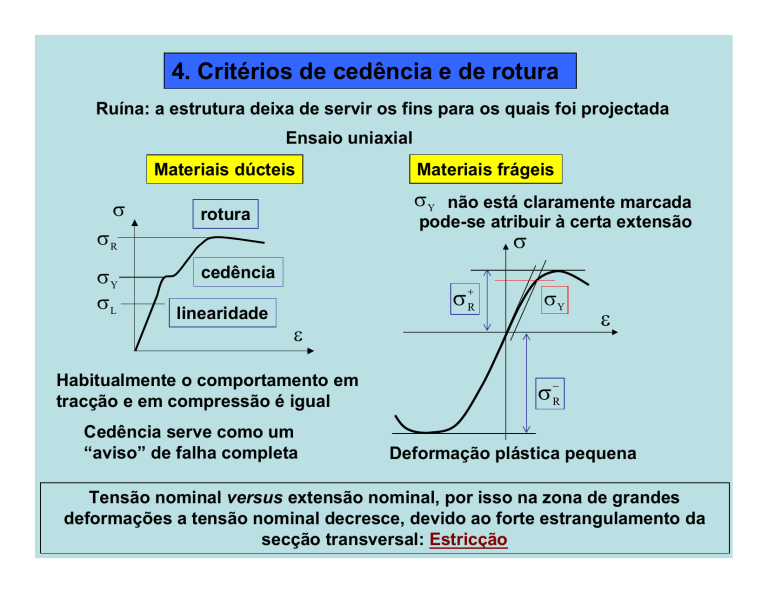
4. Critérios de cedência e de rotura
Ruína: a estrutura deixa de servir os fins para os quais foi projectada
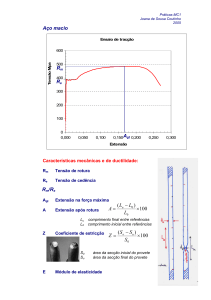
Ensaio uniaxial
Materiais dúcteis
σ
σR
σY
σL
Materiais frágeis
σ Y não está claramente marcada
rotura
pode-se atribuir à certa extensão
σ
cedência
linearidade
σ +R
σY
ε
Habitualmente o comportamento em
tracção e em compressão é igual
Cedência serve como um
“aviso” de falha completa
ε
σ −R
Deformação plástica pequena
Tensão nominal versus extensão nominal, por isso na zona de grandes
deformações a tensão nominal decresce, devido ao forte estrangulamento da
secção transversal: Estricção
Rotura sem
aviso, mas a
fracturação
pode ser
acompanhada
pelo ruído
Ruído
Maciços rochosos
σ
Rotura
IV
Início da fracturação
III
Início da microfracturação
II
Fracturação progressiva
rápida
I
Fechamento das fissuras
ε
solos, rochas e maciços rochosos poderão ter comportamento dúctil ou frágil
Deformação plástica:
escorregamento ao longo dos planos de tensão de corte máxima
falha em tracção
P
P
Material frágil
sensível à tracção
falha em compressão
Material frágil
sensível à compressão
falha em corte
Material dúctil
sensível ao corte
P
P
falha em corte
Ruína
Materiais dúcteis: cedência
Materiais frágeis: rotura
Dificuldades na determinação:
Estado tridimensional e não unidimensional
Não podemos ensaiar o provete em todas as possíveis direcções
Material isotrópico tem comportamento igual em todas as direcções, mas isso
não significa que a ruína ocorre também nas mesmas condições (folha anterior)
Materiais ortotrópicos comportam-se diferente não direcções diferentes e por
isso também limites de cedência e de rotura dependem da direcção
σ3
Superfície de cedência e de rotura
Materiais isotrópicos têm que ter a superfície de
cedência e de rotura com simetria hexagonal nos
planos // ao octaédrico (perpendiculares ao eixo do I
octante (3D)), simétrica pelo eixo do I quadrante (2D)
Materiais perfeitamente plásticos têm a
superfície de cedência e de rotura coincidente
σ1
σ2
rotura
cedência
Além das dificuldades na determinação da superfície de cedência e de rotura
tem que se considerar os factores de incerteza no carregamento, propriedades
(defeitos), dimensões, modelo e tipo de análise, tipo de falha, ... , factor de risco
Não se pode dimensionar à ruína absoluta
σ lim
σ adm
tensão limite
tensão admissível
Coeficiente de segurança:
no caso linear significa quantas vezes pode-se aumentar a carga
proporcionalmente até chegar a falha absoluta do material
σ lim
n=
σ adm
além das condições limites para as tensões existem
condições limites para as deformações
Em termos das tensões
Coulomb
σ ±max ≤ σ Y
σ
σ
σ Y−
−
≤ σi ≤
n
n
i = 1,2,3
−
Y
σ +Y
Critérios
m. isotrópicos
σ3
σi − ν (σ j + σ k ) ≤ σ Y / n
σ3
∀i ≠ j ≠ k
+
Y
tensão normal máxima
Em termos das deformações
σ +Y σ1
σ −Y
σY
Saint-Vénant
±
ε max
≤ σY / E
deformação normal máxima
σ1
σY
ν
Mohr-Coulomb
falha
σ
σ3 ≥ 0 ⇒ σ1 ≤
n
+
Y
σ3
τ xy
σ +Y σ1
−
Y
φ
σ −Y
tan φ =
2 σ −Y σ +Y
σ 2 = −τ xy
τ = c − σ tan φ
φ ângulo de
fricção interna
σV
c
σ +Y
σ Y−
σ1 (1 + sin φ) − σ3 (1 − sin φ) ≤ 2c cos φ
σ −Y − σ +Y
τ xy
E. tangencial puro
coesão
σ1 σ3 1
− − ≤
+
σY σY n
σ1 = τ xy
τ xy
τR
σ
σ −Y
σ1 ≤ 0 ⇒ σ3 ≤
n
σ
+
Y
τ xy
Cap. 1
1
c=
σ −Y σ +Y
2
σ −Y =
τ
σ −Y σ +Y
c
σV =
= −
tan φ σ Y − σ +Y
2c(1 + sin φ)
2c(1 − sin φ)
σ +Y =
cos φ
cos φ
φ = 0º
Tresca
tensão de corte máxima
τ max ≤ σ Y / 2
σY
σ1 − σ 3 ≤
n
Ocorrência de falha não
aumenta com a
diminuição de pressão
σ3
σY
σ1
φ = 90º
São casos particulares do critério Mohr-Coulomb
Tresca
Energia de distorção máxima
σ vM ≤
σY
n
1+ ν
1 2
Wd = −
σY
I′2 =
E
6G
σ +Y
σ1
σ +Y
σ1 ≤
n
σ3
von Mises
σ3
Rankine
von Mises
σY
σ1
Vistas nos planos // com o octaédrico
σ3
σ3
Rankine
Superfície
fechada
σ1
σ2
σ1
Mohr-Coulomb
σ2
σ3
σ1 = σ 2 = σ3
Cilindros infinitos
rotura
Tresca
σ1
σ2
Von Mises
σ3
σ3
σ2
σ1
σ1
σ2
cedência
Tensor
esférico
(responsável
pela alteração
de volume)
não afecta a
cedência