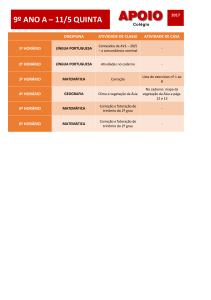
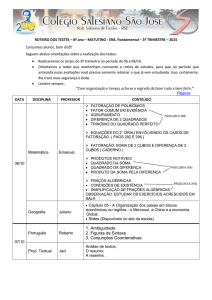
R domínio de fatoração única implica R[x] também

R domínio de fatoração única implica
R[x] também
Pedro Manfrim Magalhães de Paula
4 de Dezembro de 2013
Denição 1. Um domínio integral R com unidade é um domínio de fatoração
única
se
1. Todo elemento não nulo em R é uma unidade ou pode ser escrito como
um produto nito de elementos irredutíveis de R.
2. A decomposição da parte (1) é única a menos de ordem e associados
dos elementos irredutíveis.
A partir deste ponto assumiremos que todos os anéis R são domínios de
fatoração única.
Já sabemos que anéis euclidianos são domínios de fatoração única. O
oposto não ocorre pois, como veremos mais adiante, o anel F [x1 , x2 ] para um
corpo F é um domínio de fatoração única que não é anel euclidiano (pois não
é um domínio de ideais principais).
Em anéis comutativos podemos falar de maiores divisores comum, mas
nem sempre podemos armar que estes existem. Em domínios de fatoração
única podemos garantir esta existência pelo lema a seguir.
Lema 1.
R.
Se
Ainda
temos
a, b ∈ R,
mais, se a
então
e
b
a
e
b
possuem um maior divisor comum
são coprimos
((a, b) = 1),
então sempre
(a, b) ∈
que a|bc
a|c.
Suponha que a = r1 ...rk ...rn e b = s1 ...sk ...sm é uma decomposição de a e b tal que ri , si são associados para i ≤ k , e ri , sj não são
associados ∀i, j > k , onde k ≥ 0 (sempre podemos arranjar as fatorações de
a e b para serem desta forma).
Dena d = r1 ...rk (para k = 0 tomamos d = 1), então d divide a e b.
Seja c divisor comum de a e b. Se c - d, temos que a fatoração de c possui
um irredutível f que não divide d. Então f divide algum ri e algum sj
Demonstração.
1
para i, j > k , assim f é uma unidade ou ri e sj são associados que é uma
contradição. Portanto c|d e assim d é maior divisor comum de a e b.
Suponha que (a, b) = 1 e a|bc. Se a é unidade temos a|c. Se a = r1 ...rk não
é unidade, então existe f = s1 ...sl ∈ R tal que (p1 ...pn )(q1 ...qm ) = bc = f a =
(s1 ...sl )(r1 ...rk ), onde os pi , qi , ri , si são todos irredutíveis. Pela unicidade das
fatorações e como nenhum ri divide nenhum pj , temos que para cada ri existe
um qj associado. Logo a|c.
Corolário 1.
Se
a∈R
é um elemento irredutível e
a|bc,
então
a|b
ou
a|c
(todo irredutível é primo).
Se b = r1 ...rn e c = s1 ...sm é a decomposição de b e c em
irredutíveis, então a|bc ⇒ bc = da para algum d = t1 ...tk ∈ R. Logo
r1 ...rn s1 ...sm = t1 ...tk a, e pela unicidade da decomposição temos que a = ri
para algum i ou a = sj para algum j . Portanto a|b ou a|c.
Demonstração.
Queremos agora mostrar um análogo do Lema de Gauss para o anel R[x]
quando R é um domínio de fatoração única. Para isso precisamos denir o
que seria um polinômio primitivo.
Denição 2. Dado f (x) = a0 + a1 x + ... + am xm em R[x] denimos o con-
de f (x) como o conjunto dos maiores divisores comum de a0 , ..., am .
Denotamos este conjunto por c(f ).
teúdo
Como todo domínio de fatoração única é um domínio integral, temos que
todos os maiores divisores comuns são associados. Logo o conteúdo de um
polinômio f (x) = a0 + a1 x + ... + am xm é formado pelos associados de um
maior divisor comum de a0 , ..., am .
Denição 3. Um polinômio em R[x] é dito
conjunto das unidades.
primitivo
se seu conteúdo é o
Se f (x) ∈ R[x], é fácil ver que podemos escrever f (x) = af1 (x), onde
a ∈ c(f ) e f1 (x) é primitivo, e que esta decomposição é única a menos de
associados de a e f1 (x).
Lema 2.
O produto de polinômios primitivos em
primitivo em
R[x]
é ainda um polinômio
R[x].
Sejam p(x) = a0 +...+an xn e q(x) = b0 +...+bm xm e suponha
que o lema seja falso. Então todos os coecientes de p(x)q(x) seriam divisíveis
por um elemento de R que não é uma unidade, e assim seriam divisíveis por
um irredutível d de R. Como p(x) é primitivo, d não divide algum ai . Seja
aj o primeiro coeciente de p(x) que não é divisível por d, e analogamente
seja bk o primeiro coeciente de q(x) que não é divisível por d. Para p(x)q(x)
o coeciente de xj+k é
Demonstração.
2
cj+k = aj bk + (aj+1 bk−1 + ... + aj+k b0 ) + (aj−1 bk+1 + ... + a0 bj+k )
Pela escolha de aj e bk , d|ai para i < j e d|bi para i < k , então d|(aj−1 bk+1 +
... + a0 bj+k ) e d|(aj+1 bk−1 + ... + aj+k b0 ). Pela suposição d|cj+k , logo d|aj bk
contradição pois d - aj e d - bk . Portanto temos o resultado.
Corolário 2.
Se f (x), g(x) ∈ R[x],
{ab/a ∈ c(f ), b ∈ c(g)}.
então
c(f g) = c(f )c(g),
onde
c(f )c(g) =
Podemos escrever f (x) = af1 (x) e g(x) = bg1 (x), onde a ∈
c(f ), b ∈ c(g) e f1 (x),g1 (x) são primitivos. Então f (x)g(x) = abf1 (x)g1 (x),
e pelo Lema 2, f1 (x)g1 (x) é primitivo. Logo o conteúdo de f (x)g(x) contém
ab, e como c(f )c(g) contém todos os associados de seus elementos, temos
c(f g) = c(f )c(g).
Demonstração.
Por indução temos que o corolário se estende para um produto nito de
polinômios, assim c(f1 ...fn ) = c(f1 )...c(fn ).
Como R é um domínio de fatoração única (em particular um domínio
integral), R possui corpo de frações F . Assim podemos considerar R[X]
como um subanel de F [x]. Se f (x) ∈ F [x], então f (x) = a−1 f0 (x), onde
f0 (x) ∈ R[X] e a ∈ R.
Lema 3.
de
R[x]
Se
f (x) ∈ R[x]
se e somente se
é primitivo, então
f (x)
f (x)
é irredutível como elemento
é irredutível como elemento de
F [x].
(⇒) Suponha que f (x) é irredutível em R[x] mas é redutível
em F [x]. Então f (x) = g(x)h(x), onde g(x), h(x) ∈ F [x] e possuem grau
positivo. Sabemos que g(x) = a−1 g0 (x), h(x) = b−1 h0 (x), onde a, b ∈ R
e g0 (x), h0 (x) ∈ R[x]. Temos também que g0 (x) = αg1 (x), h0 (x) = βh1 (x),
onde α ∈ c(g0 ), β ∈ c(h0 ) e g1 (x), h1 (x) são primitivos em R[x]. Logo f (x) =
( αβ
)g1 (x)h1 (x), ou seja, abf (x) = αβg1 (x)h1 (x). Pelo Lema 2, g1 (x)h1 (x) é
ab
primitivo, assim ab ∈ c(abf ) = c(αβg1 h1 ) 3 αβ . Portanto existe u ∈ R
unidade tal que f (x) = ug1 (x)h1 (x), mas essa fatoração não é trivial já que
o grau(g1 ) = grau(g) > 0, grau(h1 ) = grau(h) > 0 e as unidades de F [x]
não possuem grau positivo (contradição).
(⇐) Suponha que f (x) é irredutível em F [x] e f (x) = p(x)q(x) em R[x].
Então f (x) = p(x)q(x) em F [x], já que R[x] é subanel de F [x]. Logo p(x)
ou q(x) é unidade em F [x]. Como F é domínio integral, as unidades de F [x]
são as unidades de F , assim p(x) ∈ F ou q(x) ∈ F . Mas p(x), q(x) ∈ R[x],
então p(x) ou q(x) é unidade de R. Logo f (x) é irredutível em R[x].
Demonstração.
Lema 4.
Se
p(x)
é um polinômio primitivo em
R[x],
então ele pode ser
fatorado de maneira única como um produto de elementos irredutíveis em
R[x].
3
Considerando p(x) como elemento de F [x], podemos fatorálo como p(x) = p1 (x)...pn (x), onde p1 (x),...,pn (x) são polinômios irredutíveis
em F [x]. Como pi (x) = a−1
i fi (x), onde fi (x) ∈ R[x] e ai ∈ R; e mais,
fi (x) = ci qi (x), onde ci ∈ c(fi ) e qi (x) é primitivo em R[x]. Temos que para
cada i, pi (x) = acii qi (x), onde ai , ci ∈ R e qi (x) é primitivo. Como pi (x) é
irredutível em F [x], qi (x) deve ser irredutível em F [x], logo pelo Lema 3,
qi (x) é irredutível em R[x]. Então
Demonstração.
p(x) = p1 (x)...pn (x) =
c1 ...cn
q (x)...qn (x)
a1 ...an 1
assim a1 ...an p(x) = c1 ...cn q1 (x)...qn (x). Usando primitividade de p(x) e de
q1 (x)...qn (x), temos que o conteúdo da parte esquerda possui a1 ...an e da
direita possui c1 ...cn . Logo a1 ...an e c1 ...cn são associados, e assim existe
unidade u ∈ R tal que p(x) = uq1 (x)...qn (x). Temos então uma fatoração de
p(x) em R[x] como um produto de irredutíveis.
A fatoração é única pois se p(x) = r1 (x)...rm (x), onde cada ri (x) é irredutível em R[x], temos por primitividade de p(x) que cada ri (x) é primitivo, e
assim irredutível em F [x] pelo Lema 3. Mas F [x] é um domínio de fatoração
única, logo os ri (x) são iguais aos qi (x) (a menos de associados) em alguma
ordem. Portanto p(x) tem uma fatoração única como produto de irredutíveis
em R[x].
Teorema. R[x] é domínio de fatoração única.
Seja p(x) ∈ R[x], podemos escrever p(x) = cp1 (x), onde c ∈
c(p) ⊂ R e p1 (x) ∈ R[x] é primitivo. Pelo Lema 4 podemos decompor p1 (x)
em um produto de irredutíveis em R[x] de maneira única. Se c = a1 (x)...an (x)
em R[x], temos que 0 = grau(c) = grau(a1 (x)) + ... + grau(an (x)). Logo
cada ai (x) tem grau 0, ou seja, é elemento de R. Assim as únicas fatorações
de c em R[x] são as formadas por elementos de R. Como R é domínio de
fatoração única, existe uma única fatoração de c como produto de irredutíveis
em R, e consequentemente em R[x].
Pela unicidade da fatoração de p(x) em cp1 (x) e pela unicidade das fatorações de p1 (x) e c, temos o resultado.
Demonstração.
Corolário 3. R[x1 , ..., xn ] é domínio de fatoração única.
Usando o fato de R ser domínio de fatoração única temos
que R[x1 ] também é, como R[x1 , x2 ] = R[x1 ][x2 ] usamos indução e temos o
resultado.
Demonstração.
Corolário 4. Se F
é corpo, então
F [x1 , ..., xn ] é domínio de fatoração única.
4
Bibliograa
[1] I. N. Herstein
Topics in Algebra,
JOHN WILEY & SONS, pp. 163 - 166
5