Intervalos. Partiç˜oes. Funç˜oes em Escada 1 Definiç˜oes

Instituto Superior Técnico
Departamento de Matemática
Secção de Álgebra e Análise
Prof. Gabriel Pires
Intervalos. Partições. Funções em Escada
1
Definições
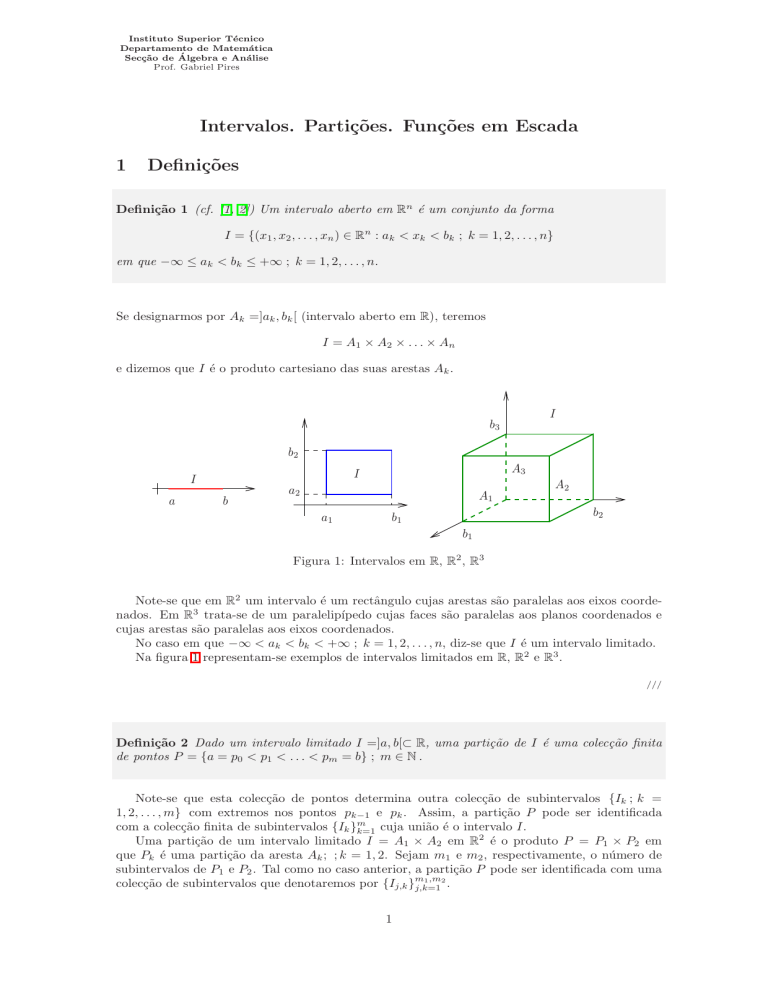
Definição 1 (cf. [1, 2]) Um intervalo aberto em Rn é um conjunto da forma
I = {(x1 , x2 , . . . , xn ) ∈ Rn : ak < xk < bk ; k = 1, 2, . . . , n}
em que −∞ ≤ ak < bk ≤ +∞ ; k = 1, 2, . . . , n.
Se designarmos por Ak =]ak , bk [ (intervalo aberto em R), teremos
I = A1 × A2 × . . . × An
e dizemos que I é o produto cartesiano das suas arestas Ak .
I
b3
b2
a
A3
I
I
b
a2
A1
a1
A2
b2
b1
b1
Figura 1: Intervalos em R, R2 , R3
Note-se que em R2 um intervalo é um rectângulo cujas arestas são paralelas aos eixos coordenados. Em R3 trata-se de um paralelipı́pedo cujas faces são paralelas aos planos coordenados e
cujas arestas são paralelas aos eixos coordenados.
No caso em que −∞ < ak < bk < +∞ ; k = 1, 2, . . . , n, diz-se que I é um intervalo limitado.
Na figura 1 representam-se exemplos de intervalos limitados em R, R2 e R3 .
///
Definição 2 Dado um intervalo limitado I =]a, b[⊂ R, uma partição de I é uma colecção finita
de pontos P = {a = p0 < p1 < . . . < pm = b} ; m ∈ N .
Note-se que esta colecção de pontos determina outra colecção de subintervalos {Ik ; k =
1, 2, . . . , m} com extremos nos pontos pk−1 e pk . Assim, a partição P pode ser identificada
com a colecção finita de subintervalos {Ik }m
k=1 cuja união é o intervalo I.
Uma partição de um intervalo limitado I = A1 × A2 em R2 é o produto P = P1 × P2 em
que Pk é uma partição da aresta Ak ; ; k = 1, 2. Sejam m1 e m2 , respectivamente, o número de
subintervalos de P1 e P2 . Tal como no caso anterior, a partição P pode ser identificada com uma
1 ,m2
colecção de subintervalos que denotaremos por {Ij,k }m
j,k=1 .
1
I
Ijk
Figura 2: Partição de um intervalo em R2
Na figura 2 representa-se uma partição de um intervalo em R2 .
Do mesmo modo, dado um intervalo limitado I = A1 × A2 × A3 em R3 , uma partição de I é
o produto P = P1 × P2 × P3 em que Pk é uma partição da aresta Ak ; ; k = 1, 2, 3. Tal como nos
1 ,m2 ,m3
.
casos anteriores, podemos identificar P com uma colecção de subintervalos {Ijkl }m
j,k,l=1
Assim, de uma forma geral, uma partição de um intervalo limitado I pode ser definida por
uma colecção de subintervalos {Ik }N
k=1 em que N < ∞ tais que
I = ∪N
k=1 Ik
3
0
.5
1
−2
Figura 3: Exemplo de uma função em escada em R
///
Definição 3
• Seja I ⊂ Rn um intervalo limitado. Diz-se que s : I → R é uma função
em escada em I se existir uma partição de I , {Ik }N
k=1 e uma colecção de números reais
{sk }N
,
tais
que
s(x)
=
s
se
x
∈
int(I
)
,
em
que
int(I
k
k
k ) designa o interior de Ik .
k=1
• Seja I ⊂ Rn um intervalo não limitado. Diz-se que s : I → R é uma função em escada
em I se existir um intervalo limitado J ⊂ I tal que s é uma função em escada em J e toma
o valor zero em I \ J.
2
///
Definição 4 Dado um intervalo limitado, I ⊂ Rn , chama-se volume de I à quantidade
vol(I) =
n
Y
(bi − ai )
i=1
0
6
1
6
Figura 4: Exemplo de uma função em escada em R2
Definição 5 Dada uma função em escada, s : I → R, chama-se integral de s em I à quantidade
Z
I
2
s=
N
X
s vol(Ik )
k
k=1
Exemplos
i) Seja I =]0, 1[⊂ R e s : I → R a função, cujo gráfico se apresenta na figura 3, definida por

se 0 < x < 12
 1,
3,
se 21 < x < 23
s(x) =

−2 se 32 < x < 1
Trata-se de uma função em escada cujo integral é dado por
Z
2 1
2
1 1 2
1
1
s = 1 × + 3 × ( − ) − 2 × (1 − ) = + − =
2
3 2
3
2 2 3
3
I
///
ii) Seja I =]0, 6[2 =]0, 6[×]0, 6[⊂ R2 e s : I → R a função em escada dada por

4 se 0 < x < 1 ; 0 < y < 1




 2 se 0 < x < 1 ; 1 < y < 2
1 se 3 < x < 6 ; 1 < y < 2
s(x, y) =


4 se 3 < x < 6 ; 5 < y < 6



0
nos restantes casos
3
cujo gráfico se apresenta na figura 4.
O integral de s em I é dado por
Z
s = 4 + 2 + 1 + 1 + 1 + 4 + 4 + 4 = 21
I
///
iii) Seja I =]0, 1[×]0, 2[×]1, 2[⊂ R3 e s : I → R dada por
1 se 0 < x < 1 ; 0 < y < 2 ; 1 < z < 23
s(x, y, z) =
2 se 0 < x < 1 ; 0 < y < 2 ; 23 < z < 2
O integral de s em I é dado por
Z
1
1
s=1×1×2× +2×1×2× =3
2
2
I
Referências
[1] Luı́s T. Magalhães. Integrais Múltiplos. Texto Editora, 1996.
[2] H. A. Priestley. Introduction to Integration. Oxford, Clarendon Press, 1997.
4