universidade federal do amazonas - OptiMa-UFAM

UNIVERSIDADE FEDERAL DO AMAZONAS
INSTITUTO DE CIÊNCIAS EXATAS
DEPARTAMENTO DE FÍSICA
______________________________________________________
Laboratório de Física Moderna
1. Título: Dispersão do cristal de quartzo
2. Objetivo:
•
Determinar a relação de dispersão do cristal de quartzo.
3. Introdução Teórica:
A decomposição da luz branca em cores por um prisma (Fig. 1) é devida à
dispersão, isto é, ao fato que o índice de refração depende do comprimento de onda.
A fórmula que relaciona o índice de refração com o comprimento de onda denominase relação de dispersão e o objetivo deste experimento é determinar a relação de
dispersão do quartzo de um prisma.
.
Fig.1. Dispersão por um prisma.
A dispersão da luz se manifesta em fenômenos naturais, como o arco íris, e em
vários campos da ciência e tecnologia. Por exemplo, em lentes dá lugar à aberração
cromática e, em comunicações por fibra óptica, produz um alargamento dos pulsos de
luz que se propagam nas fibras, limitando a taxa de transmissão. Assim, conhecer a
relação de dispersão é importante para projetar lentes de câmeras, telescópios e
microscópios e sistemas de comunicação óptica.
Na região do espectro visível, na maioria dos materiais o índice de refração
diminui com o comprimento onda (este comportamento se diz dispersão normal; se
dn/dλ > 0 se diz dispersão anômala) e, portanto, luz vermelha viaja mais rápido que luz
azul.
Uma forma de descrever a dispersão da luz em um meio é empregando a
equação de Sellmeyer (Eq. 1). É uma relação empírica entre o índice de refração e o
comprimento de onda para um meio transparente:
1
1
⁄
1
⁄
.1
Com esta equação, podemos obter das medidas um ajuste adequado para os
coeficientes (A1, B1, A2, B2) da equação de Sellmeyer, permitindo obter o índice de
refração com boa precisão.
Os valores de n podem ser medidos usando-se um prisma do material de
interesse com um canto de ângulo , chamado de ângulo refrator (fig. 2), e
determinando-se o ângulo de desvio mínimo
do raio de luz com o espectroscópio,
empregando a relação
2
2
Fig. 2. Desvio de um raio de luz por um prisma.
4. Parte Experimental:
•
Material necessário:
• Espectroscópio (fig.3)
• Fonte luminosa
• Prisma de quartzo
Fig. 3. Espectroscópio e seus componentes
.2
•
Procedimento experimental
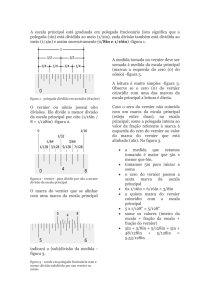
1) Alinhamento inicial: (utilize luz branca ou qualquer lâmpada)
a) Destrave a trava do telescópio e alinhe a fenda de entrada de luz com o
telescópio de leitura. Ajuste o foco do telescópio observando a fenda. Coloque um
papel branco entre o prisma e telescópio e ajuste o foco da ocular observando a cruz
(a lente ocular desliza, não é parafusada). A fenda e a cruz devem aparecer nítidas no
campo visual. Atenção: o foco depende do olho de cada pessoa.
b) Trave o telescópio e faça o ajuste fino com o parafuso de avanço da base
giratória. Atenção: a linha vertical da cruz deve coincidir com o lado da fenda que não
se move.
c) Uma vez alinhado, solte a trava do vernier e ajuste o "zero" da escala bem
perto do "zero" do Vernier. Trave o espectroscópio e com ajuda da lupa para ver bem
os riscos no Vernier, ajuste o “zero” movendo o espectroscópio com o ajuste fino do
Vernier.
2) Medida do ângulo refrator do prisma
Para medir usamos o fato que o ângulo entre os dois raios refletidos nas duas faces
do prisma é sempre igual a 2 (fig. 4).
a) Destrave o telescópio.
b) Coloque o prisma com o ápice apontado para a fenda e procure a imagem
refletida em uma das faces do prisma. Reajuste o foco da luneta.
c) Se a imagem da fenda não estiver paralela à linha vertical da cruz, gire
levemente a fenda até alinhá-la corretamente.
d) Procure a imagem refletida na outra face do prisma.
e) As imagens vistas por reflexão nas duas faces do prisma devem estar à
mesma altura no campo visual. Se isto não acontece é porque o prisma está inclinado.
Caso isto não ocorra deve nivelar mesa de amostra.
f) Alinhe com uma das reflexões e verifique em cada imagem refletida qual é o
lado da fenda que não se move.
g) Trave o telescópio e alinhe finamente (parafuso de avanço da base giratória)
a cruz com o lado da fenda que não se move. Faça a leitura dos ângulos (L1 e L2) no
Vernier correspondente às duas reflexões. Atenção: uma das leituras (por exemplo,
L1) coincide com o ângulo defletido na reflexão enquanto que a outra (por exemplo,
L2) deve ser subtraída de 360º: = (L1+ 360º - L2)/2.
Fig. 4. Esquema para medir .
3) Achando o ângulo de desvio mínimo:
a) Posicione o prisma de modo que os raios refratados se dirijam para o lado dos
ângulos “positivos” (para não ter de subtrair 360º em toda medida).
b) Destrave o telescópio e ache a raia amarela. Ajuste o foco e feche a fenda até obter
uma imagem nítida e o mais fina possível.
c) Destrave a mesa da amostra ligeiramente de modo que a mesma possa girar sem
cair. Gire a mesa do prisma com uma mão e acompanhe a raia amarela movendo o
telescópio com a outra mão até achar a posição em que o desvio é mínimo.
d) Trave o telescópio e a mesa.
e) Utilizando o avanço fino do telescópio, alinhe a linha vertical da cruz com o lado da
imagem da fenda que não se move e leia o ângulo no Vernier. Agora você já tem uma
medida de desvio para esse comprimento de onda,
.
f) Para medir outras linhas, siga sempre a mesma rotina: destrave telescópio; mova-o
até chegar perto da linha; trave o telescópio e alinhe com o “fino”.
•
Tratamento de Dados:
• Organize os dados numa tabela: cor, comprimento de onda, desvio
angular , índice de refração (n) calculado através da Eq. 2.
• Trace um gráfico de n versus .
• Ajuste a equação de Sellmeyer aos pontos experimentais e obtenha os
coeficientes A1, B1, A2, B2...
• Questões:
1) Observando a figura 5 e usando a lei de Snell na primeira refração, obtenha a
equação 2.
Fig. 5. Desvio de um raio de luz por um prisma (esquerda) como soma dos desvios na
primeira e na segunda refração (direita).
OBS: Não se esqueça de sempre avaliar e apresentar os erros para cada
resultado apresentado.