referenciais em translação

Objetivos
Introduzir os conceitos de posição, deslocamento,
velocidade e aceleração
Estudar o movimento de um ponto material ao longo
de uma reta e representar graficamente esse
movimento
Investigar o movimento de um ponto material ao
longo de uma trajetória curva usando diferentes
sistemas de coordenadas
Apresentar uma análise do movimento
interdependente de dois pontos materiais
Examinar os princípios do movimento relativo de dois
pontos materiais usando eixos em translação
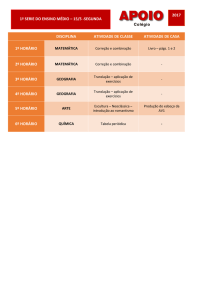
MECÂNICA - DINÂMICA
Cinemática de uma
Partícula
Cap. 12
Prof Dr. Cláudio Curotto
Adaptado por:
Prof Dr. Ronaldo Medeiros-Junior
TC027 - Mecânica Geral III - Dinâmica
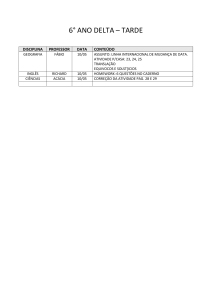
12.10 Análise do Mov. Rel. de Dois Ptos. Mat. Usando-se Ref. em Translação
2
12.10 Análise do Mov. Rel. de Dois Ptos. Mat. Usando-se Ref. em Translação
Posição
Único referencial fixo para determinar o movimento
E se for necessário utilizar dois ou mais sistemas de referência?
Movimento da ponta da hélice
de um avião em vôo
Considere dois pontos materiais, A e B, que se movem ao longo de trajetórias
arbitrárias aa e bb, respectivamente. A posição absoluta de cada ponto material,
rA e rB, é medida em relação à origem comum O do sistema de referência fixo x,
y, z. A origem de um segundo sistema de referência x’, y’, z’ é ligada ao ponto
material A e, portanto, se move com ele. A ‘posição de B em relação a A’ é
indicada pelo vetor de posição relativa rB/A. Por adição vetorial, os três vetores
de posição podem ser relacionados pela equação:
rB = rA + rB / A
Será analisado a seguir
referenciais em translação
TC027 - Mecânica Geral III - Dinâmica
12.10 Análise do Mov. Rel. de Dois Ptos. Mat. Usando-se Ref. em Translação
D
E
R
I
V
A
N
D
O
TC027 - Mecânica Geral III - Dinâmica
3
12.10 Análise do Mov. Rel. de Dois Ptos. Mat. Usando-se Ref. em Translação
D
E
R
I
V
A
N
D
O
Posição
rB = rA + rB / A
Velocidade
vB = vA + vB / A
4
Velocidade
vB = vA + vB / A
Aceleração
aB = aA + aB / A
Velocidades absolutas
Velocidade relativa
Acelerações absolutas
Aceleração relativa
(observadas do referencial fixo)
(observadas do referencial em translação)
(observadas do referencial fixo)
(observadas do referencial em translação)
Obs.: A velocidade de B é igual à soma vetorial da velocidade de A
com a velocidade de ‘B em relação a A’, medida pelo observador
fixo no referencial em translação x’, y’, z’.
TC027 - Mecânica Geral III - Dinâmica
5
TC027 - Mecânica Geral III - Dinâmica
6
1
Exemplo 12.25
Exemplo 12.25 - Solução
vT = v A + vT / A
Um trem, viajando com velocidade constante de 60 milhas/h, cruza uma
rodovia. Se um automóvel A está a 45 milhas/h ao longo da rodovia,
determine o módulo, a direção e o sentido da velocidade relativa do trem
em relação ao automóvel.
28,2i
vT = 60i
ϴ
2
v A = 45cos 450 i + 45sen 450 j
{
vT / A = 28, 2 + ( −31,8)
31,8j
2
vT / A = 42,5 milhas/h
}
60i = 45cos 450 i + 45sen 450 j + vT / A
vT / A = {28, 2i − 31,8 j} milhas/h
tg θ =
( vT / A ) y
( vT / A ) x
=
31,8
= 1,1277
28, 2
θ = 48, 40
TC027 - Mecânica Geral III - Dinâmica
TC027 - Mecânica Geral III - Dinâmica
7
Exemplo 12.25
8
Exemplo 12.25
Um homem levanta um cofre B e começa a caminhar para a direita com uma
velocidade constante vA = 0,5 m/s, como mostrado na figura. Determine a
velocidade e aceleração do cofre quando ele alcança a altura de 10 m. A corda
tem 30 m de comprimento e passa sobre uma pequena polia em D.
-A posição da extremidade C da corda (e consequentemente a posição do cofre
B) é dada pela coordenada y.
-A posição da extremidade A da corda é dada pela coordenada x.
-Ambas são medidas a partir de um referencial fixo e direcionados ao longo das
trajetórias de movimento das extremidades da corda.
-O comprimento total da corda (=30 m)
é dado pela soma dos seguimentos CD +
DA
l = CD + DA = 30
B
B
TC027 - Mecânica Geral III - Dinâmica
TC027 - Mecânica Geral III - Dinâmica
9
Exemplo 12.25
10
Exemplo 12.25
Derivada temporal:
l = CD + DA = 30
(15 − y ) + ( 225 + x
(
y = 225 + x
2 1/2
)
2 1/2
)
y =
= 30
CD = 15 − y
Por Pitágoras:
2
DA = 15 + x
Derivada temporal:
(
1/2
)
1
y = 225 + x 2
2
(
(
Como:
− 15
2
y = 225 + x 2
1
2
225 + x
2
y = vB
)
2
DA = 225 + x 2
− 15
−1/2
)
−1/2
2 xx
x = vA
Logo:
(
vB = 225 + x 2
)
−1/2
xv A
B
B
2 xx
TC027 - Mecânica Geral III - Dinâmica
11
TC027 - Mecânica Geral III - Dinâmica
12
2
Exemplo 12.25
(
vB = 225 + x
2 −1/2
)
Exemplo 12.25
(
vB = 225 + x
xv A
De acordo com a Equação abaixo,
para y =10 m, x = 20m.
1/2
(
)
10 = ( 225 + x )
y = 225 + x 2
2
vB = −
(
− 15 ∴ 225 + x 2
1/2
)
Como:
B
Voltando para a equação das velocidades,
e considerando vA = 0,5 m/s e x = 20m.
(
vB = 225 + 20
)
xv A
1
225 + x 2
2
(
)
−3/2
(
2 xx ( xv A ) + 225 + x 2
)
−1/2
(
2
x ( v A ) + 225 + x
)
−1/ 2
xvA
= 25
x 2 = 252 − 225 ∴ x = 20m
2 −1/2
)
Derivando a equação da velocidade para
encontrar a aceleração:
− 15
1/2
2 −1/2
1
2
225 + ( 20 )
2
aB = 0, 0036m / s 2
aB = −
( 20 )( 0,5) = 0, 4m / s
TC027 - Mecânica Geral III - Dinâmica
vB = aB
v A = a A = 0
13
(
)
−3/2
(
2 ( 20 )( 0,5 )( 20 ⋅ 0,5 ) + 225 + ( 20 )
TC027 - Mecânica Geral III - Dinâmica
2
)
−1/ 2
(
0,5 ( 0,5 ) + 225 + ( 20 )
2
)
−1/ 2
( 20)( 0)
14
3