BA θ - Páginas Pessoais

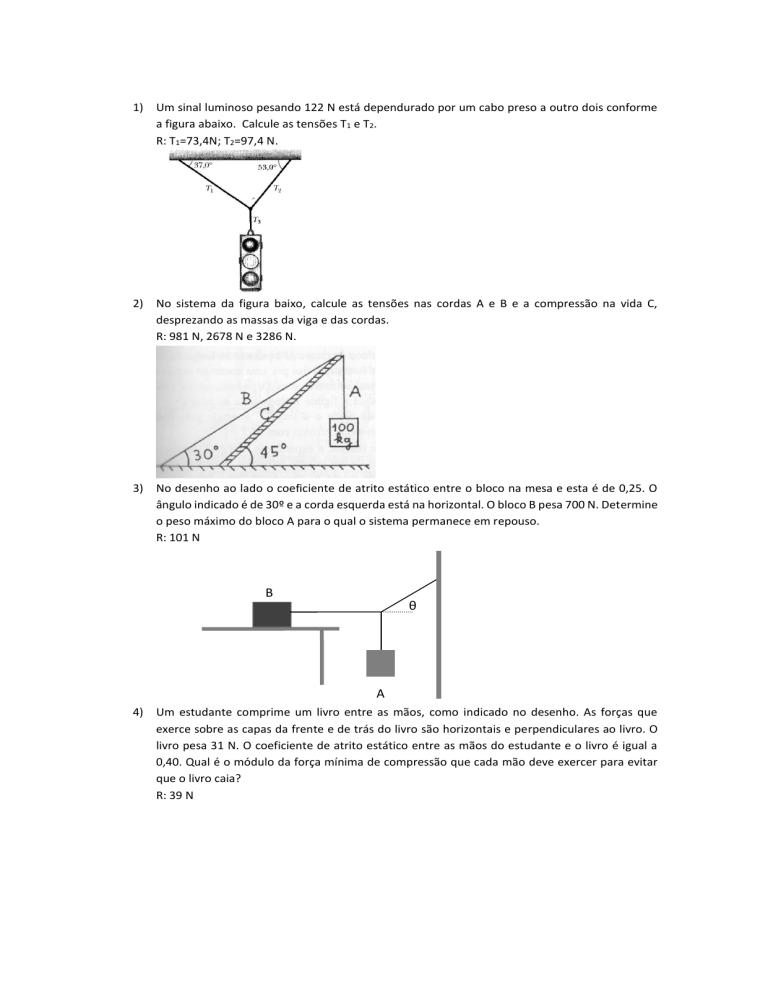
1) Um sinal luminoso pesando 122 N está dependurado por um cabo preso a outro dois conforme
a figura abaixo. Calcule as tensões T1 e T2.
R: T1=73,4N; T2=97,4 N.
2) No sistema da figura baixo, calcule as tensões nas cordas A e B e a compressão na vida C,
desprezando as massas da viga e das cordas.
R: 981 N, 2678 N e 3286 N.
3) No desenho ao lado o coeficiente de atrito estático entre o bloco na mesa e esta é de 0,25. O
ângulo indicado é de 30º e a corda esquerda está na horizontal. O bloco B pesa 700 N. Determine
o peso máximo do bloco A para o qual o sistema permanece em repouso.
R: 101 N
B
θ
A
4) Um estudante comprime um livro entre as mãos, como indicado no desenho. As forças que
exerce sobre as capas da frente e de trás do livro são horizontais e perpendiculares ao livro. O
livro pesa 31 N. O coeficiente de atrito estático entre as mãos do estudante e o livro é igual a
0,40. Qual é o módulo da força mínima de compressão que cada mão deve exercer para evitar
que o livro caia?
R: 39 N
5) Um motor de automóvel possui W, cujo módulo é 3150 N. Este motor está sendo posicionado
acima de um compartimento de motor, como ilustrado na figura abaixo. Para posicionar o motor,
um operário está usando uma corda. Determine a tração T1 no cabo de sustentação e a tração
T2 na corda de posicionamento na situação estática. R: 3300 N; 582 N.
6) Uma bala de fuzil de massa 20 g atinge uma árvore com uma velocidade de 500 m/s, penetrando
nela a uma profundidade de 10 cm. Calcule a força média exercida sobre a bala durante a
penetração.
R: 2,5 x 104 N
7) No sistema da figura abaixo, o bloco 1 tem massa de 10 kg, e o coeficiente de atrito estático com
o plano é 0,5. Entre que valores máximo e mínimo pode varia a massa m do bloco 2 para que o
sistema permaneça em equilíbrio? Indique as forças que estão agindo, indique o referencial
adequado, e use as leis de Newton de acordo com o referencial escolhido.
R:10,6 e 3,54 kg
45o
8) O peso do bloco da figura abaixo é 89 N. O coeficiente de atrito estático entre o bloco e a parede
vertical é 0,60 (a) Qual é a força mínima F necessária para impedir que o bloco deslize para baixo
na parede? (b) Qual é a força mínima F para fazer o bloco começar a se mover para cima na
parede?
R: 77N; 234 N.
9) Considere a figura abaixo:
Bloco
Mesa
Terra
(a) Identifique na figura, todas as forças que estão agindo no sistema. (b) Quais são os pares de ação
e reação?
10) Um cavalo está atrelado a uma carroça e a puxa com uma força . Por outro lado, a carroça puxa
o cavalo com uma força, de mesma intensidade e de sentido contrário. Sendo assim, por que o
cavalo se move?
11) Um bloco de massa M é puxado ao longo de uma superfície horizontal lisa por uma corda de

massa m, sobre a qual se exerce uma força F , conforme a figura. Determine a aceleração do


bloco e da corda e a força T exercida pela corda sobre o bloco. Qual é o valor de T se
desprezarmos m em confronto com M?
M

a
m





F
MF
;T 
;T  F .
( M  m)
( M  m)
12) Uma pessoa de massa 80 Kg está sobre uma balança num elevador. Qual a indicação da balança
quando o elevador: (a) sobre acelerado, com aceleração constante de 2 m/s2? (b) desce
acelerado, com aceleração constante de 2 m/s2? (c) sobe com velocidade constante? (d) cai em
queda livre (os cabos se rompem)? Faça um desenho com o diagrama de forças. (g=9,8 m/s2)
R: (a) 944 N; (b) 624 N; (c) 784 N; (d) 0 N.
13) Um veículo se move em uma trajetória retilínea sobre um plano horizontal conforme a figura
abaixo. Um pêndulo no seu interior desloca-se em relação a posição de equilíbrio e permanece
com um ângulo α com a vertical. Calcule a aceleração do veículo em função de g e α.
R: 𝑎 = 𝑔 𝑡𝑔 𝛼
14) Um jogador de basquete de 100 kg consegue saltar verticalmente até 80 cm no ar, como
mostrado na figura abaixo. Suponha uma aceleração constante durante o salto. Se o jogador
estivesse sobre uma balança que marca o peso em Newtons, quanto ela marcaria antes do salto,
durante o salto e depois do salto?
R: 2287 N
15) Uma força de 80 N è aplicada no corpo A conforme a figura abaixo. M A=2,0 kg e MB=3,0 kg.
Desprezando a resistência do ar, calcule a força que traciona o fio entre os corpos A e B.
R: 48 N
16) Um carro de 1000 Kg é freado firmemente de modo que as rodas fiquem bloqueadas, deixando
uma marca de 5 m no asfalto até que o carro pare. Suponha um asfalto seco, e que os pneus
foram bloqueados de forma idêntica. Calcule a velocidade do carro um pouco antes da freada,
supondo   0,8 . Faça um desenho com o diagrama de forças. (g=9,8m/s2)
R: 32 Km/h.
17) Um corpo de 4,5 Kg é lançado com uma velocidade inicial de 14 m/s por um plano inclinado
acima. O ângulo do plano com a horizontal é de 37o. Quando o corpo percorreu 8 m, sua
velocidade para cima caiu para 5,2 m/s. Calcule (a) o coeficiente de atrito cinético entre o corpo
e o plano, (b) a distância percorrida pelo corpo entre o ponto de partida e o instante em que fica
momentaneamente em repouso e (c) a velocidade do corpo ao atingir, de volta, o ponto inicial.
Desenhe o diagrama de forças em cada situação.
R:0,6; 9,3 m; 4,8 m/s.
18) Um bloco de 50 kg está apoiado sobre um plano inclinado de 30 o com a horizontal, conforme a
figura abaixo. O coeficiente de atrito cinético entre a rampa o bloco é 0,3. Este corpo está ligado
a outro de 30 kg por um fio inextensível através uma rolada de massa desprezível. Calcule a
aceleração do sistema e a tensão do fio.
R: 1,1 m/s2; 260 N
A
B
30o
19) O período de revolução lunar é de 27,3 dias e a distância média da Lua a Terra é de 384 399 km.
Com estes dados calcule a massa da Terra.
20) Em um parque de diversões, os passageiros de um brinquedo chamado de Rotor ficam em pé
dentro de um anel girante com 16 m de diâmetro. Depois que o anel adquiriu velocidade
suficiente, ele inclina até ficar girando no plano vertical, conforme a figura abaixo. Suponha que
o anel complete cada volta em 4,5 s. Se a massa do passageiro for de 55 kg, com que intensidade
de força o anel o empurrará no topo de uma volta? E no fundo? 3,2 x 10 2 N; 1,4 kN
21) Uma curva horizontal semicircular numa estrada tem 30 m de raio. O coeficiente de atrito
estático entre os pneus e o asfalto é 0,6, qual é a velocidade máxima com que o carro pode fazer
a curva sem derrapar? Faça um desenho com o diagrama de forças.
R: 47,8 km/h.
22) No sistema da figura abaixo, a bolinha de massa m está amarrada por fios de massa desprezível
ao eixo vertical AB e gira com velocidade angular w em torno desse eixo. A distância AB vale l.
Calcule as tensões nos fios superior e inferior. Para que valor de w o fio inferior ficaria frouxo?
Indique as forças que estão agindo, indique o referencial adequado, decomponha as forças no
eixos cartesianos, e use as leis de Newton de acordo com o referencial escolhido.
60o
A
m
30o
B
R: S:

m
3 2  m  w2
g
3 
l  g  ; wc  2
 g  w l  ; I:
2
4
2
l

 4

23) O dispositivo da figura abaixo gira em torno do eixo vertical com uma velocidade w. Qual é o
valor de w e a tensão no fio?
𝑔 𝑡𝑔 𝜃
R: 𝑤 = √(𝑑+𝑙
;𝑇=
sin 𝜃)
𝑚𝑔
cos 𝜃
.