Determinar Tp %UP e Ts com base na localização de

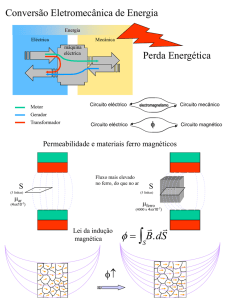
Exemplo 4.6
ADL20
Determinar Tp %UP e Ts com base na localização de pólos
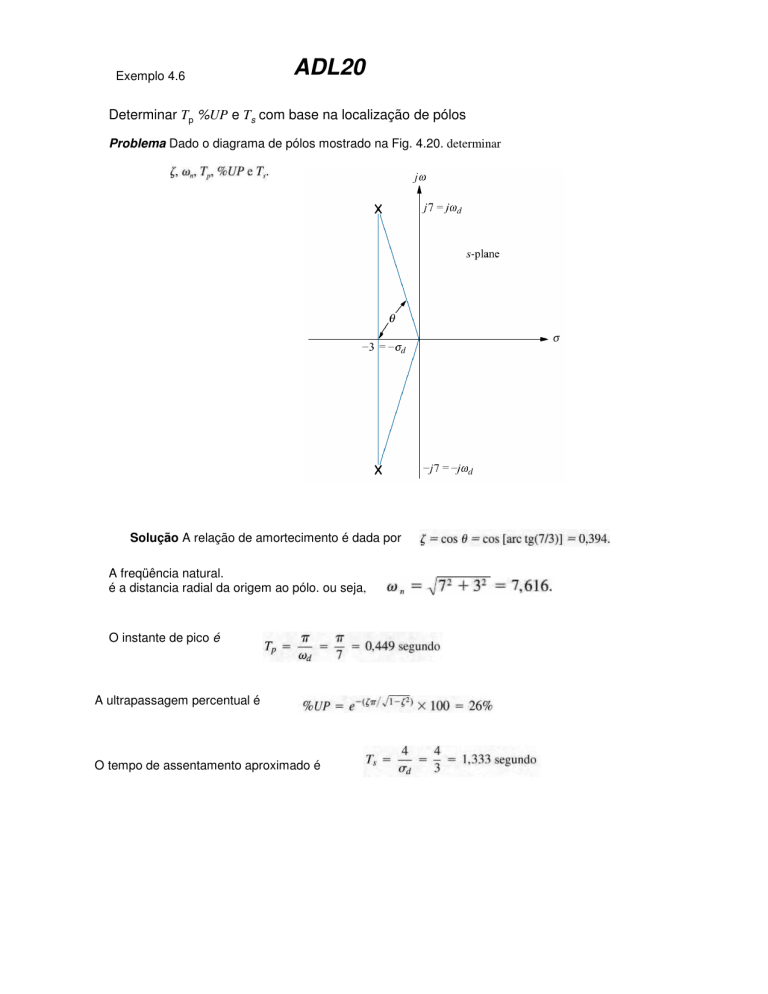
Problema Dado o diagrama de pólos mostrado na Fig. 4.20. determinar
Solução A relação de amortecimento é dada por
A freqüência natural.
é a distancia radial da origem ao pólo. ou seja,
O instante de pico é
A ultrapassagem percentual é
O tempo de assentamento aproximado é
5.3 Análise e Projeto de Sistemas com Retroação
Considere o sistema mostrado na Figura, representando um sistema de segunda ordem. A função de transferência
a malha fechada T(s) para este sistema é:
(5.10)
onde K modela o ganho do amplificador, isto é. a relação entre a tensão de saída e a tensão de entrada. À
medida que K varia, os pólos se deslocam ao longo das três faixas de operação de um sistema de segunda
ordem: superamortecido, criticamente amortecido e subamortecido. Por exemplo, para K entre 0 e a2/4, os
pólos do sistema são reais e estão situados em:
(5.11)
À medida que K aumenta, os pólos se deslocam sobre o eixo real e o sistema permanece
superamortecido até K = a2/4. Para este valor de ganho, ou esta amplificação, ambos os pólos são iguais
e o sistema é criticamente amortecido.
Para valores de ganho superiores a a2/4, o sistema é subamortecido, com pólos complexos situados
em
(5.12)
Daí em diante, à medida que K aumenta, a parte real permanece constante e a parte imaginária cresce.
Portanto, o instante de pico diminui e a ultrapassagem percentual aumenta, enquanto o tempo de
assentamento permanece constante.
Exemplo 5.3
Determinando a resposta transitória
Problema Para o sistema mostrado abaixo, obter o instante de pico, a ultrapassagem percentual e o
tempo de assentamento.
Solução A função de transferência a malha fechada obtida da Eq. (5.9) é
(5.13)
(5.14)
(5.17)
Portanto,
(5.18)
(5.19)
Usando os valores de
respectivamente,
e
n
juntamente com as Eqs. (4.34). (4.38) e (4.42), encontramos,
Exemplo 5.4
Projeto de ganho para resposta transitória
Problema Projetar o valor de ganho, K, para o sistema de controle com retroação da Fig. 5.16, de
modoque o sistema responda com uma ultrapassagem percentual de 10%.
Solução A função de transferência a malha fechada do sistema é
Da Eq, (5.20), e
Portanto,
Como a ultrapassagem percentual é função unicamente de
ultrapassagem de 10% acarreta = 0,591. Portanto, K=17,9
, e este uma função de K, uma