1 Sinais Elementares em Tempo Contínuo

ET75H - SINAIS E SISTEMAS 1 - 2sem13
Prof.: Rafael Souto - Aula 02
1 Sinais Elementares em Tempo Contínuo
1.1 Degrau Unitário
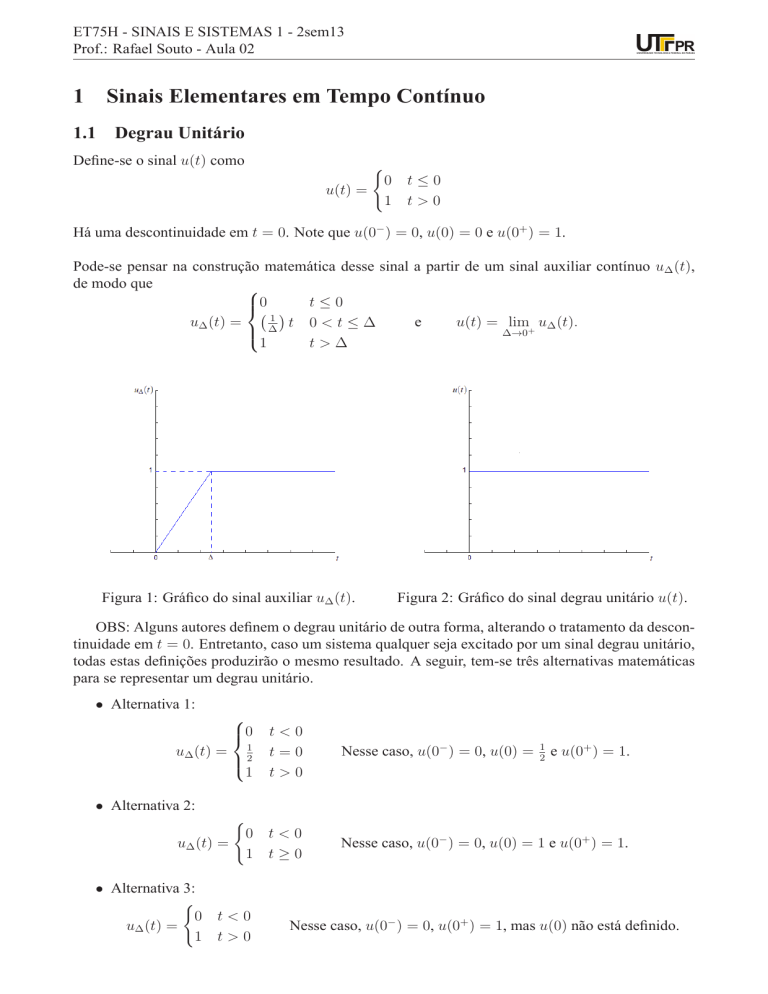
Define-se o sinal u(t) como
u(t) =
(
0
1
t≤0
t>0
Há uma descontinuidade em t = 0. Note que u(0− ) = 0, u(0) = 0 e u(0+ ) = 1.
Pode-se pensar na construção matemática desse sinal a partir de um sinal auxiliar contínuo u∆ (t),
de modo que


t≤0
0 1
e
u(t) = lim+ u∆ (t).
u∆ (t) =
t 0<t≤∆
∆

∆→0

1
t>∆
Figura 1: Gráfico do sinal auxiliar u∆ (t).
Figura 2: Gráfico do sinal degrau unitário u(t).
OBS: Alguns autores definem o degrau unitário de outra forma, alterando o tratamento da descontinuidade em t = 0. Entretanto, caso um sistema qualquer seja excitado por um sinal degrau unitário,
todas estas definições produzirão o mesmo resultado. A seguir, tem-se três alternativas matemáticas
para se representar um degrau unitário.
• Alternativa 1:
u∆ (t) =
t<0
t=0
t>0
Nesse caso, u(0− ) = 0, u(0) =
(
t<0
t≥0
Nesse caso, u(0− ) = 0, u(0) = 1 e u(0+ ) = 1.
1
2

• Alternativa 2:
u∆ (t) =
• Alternativa 3:
(
0
u∆ (t) =
1


0
1
0
1
t<0
t>0
1
2
e u(0+ ) = 1.
Nesse caso, u(0− ) = 0, u(0+ ) = 1, mas u(0) não está definido.
ET75H - SINAIS E SISTEMAS 1 - 2sem13
Prof.: Rafael Souto - Aula 02
1.2 Impulso Unitário
Define-se o sinal δ(t) a partir da seguinte caracterização
δ(t) = 0 para t 6= 0
e
Z
+∞
δ(t)dt = 1.
−∞
O sinal δ(t) não está definido em t = 0. Diz-se, então, que o impulso ocorre em t = 0 e possui área
unitária. Note que u(0− ) = 0 e u(0+ ) = 0.
Pode-se pensar na construção matemática desse sinal a partir de um sinal auxiliar δ∆ (t), obtido pela
derivada do sinal u∆ (t), de modo que


0 t ≤ 0
d
δ∆ (t) = u∆ (t) = ∆1 0 < t ≤ ∆
e
δ(t) = lim+ δ∆ (t).

∆→0
dt

0 t>∆
Figura 3: Gráfico do sinal auxiliar δ∆ (t).
Figura 4: Gráfico do sinal impulso unitário δ(t).
Nesse caso, u(0) = 0 e o impulso ocorre em t = 0+ , ficando em disacordo com a nossa caracterização
inicial para o sinal δ(t). Seria então mais consistente obter δ(t) a partir do limite de outros sinais, tais
como os mostrados nos gráficos abaixo.
Figura 5: Gráfico de um sinal auxiliar.
Figura 6: Gráfico de um sinal auxiliar.
ET75H - SINAIS E SISTEMAS 1 - 2sem13
Prof.: Rafael Souto - Aula 02
Algumas propriedades do δ(t):
Rt
• δ(t) = dtd u(t) e u(t) = −∞ δ(τ )dτ .
R +∞
• f (t)δ(t) = f (0)δ(t) e −∞ f (t)δ(t)dt = f (0), ∀f (t) contínua em t = 0.
R +∞
• f (t)δ(t − t0 ) = f (t0 )δ(t − t0 ) e −∞ f (t)δ(t − t0 )dt = f (t0 ), ∀f (t) contínua em t = t0 .
R +∞
1
1
• δ(a(t − t0 )) = |a|
δ(t − t0 ) e −∞ f (t)δ(at)dt = |a|
f (0), a ∈ R, a 6= 0.
• δ(t) pode ser considerado um sinal par.
1.3 Trem de Impulsos
Define-se o sinal δT (t) como
δT (t) =
∞
X
δ(t − nT0 )
n=−∞
Trata-se de um sinal periódico de período T = T0 , impossível de se criar fisicamente, porém utilizado
para representar matematicamente a amostragem de sinais contínuos.
Figura 7: Gráfico do sinal trem de impulsos.
1.4 Rampa Unitária
Define-se o sinal rampa(t) como
0
t
t≤0
t>0


−1
sgn(t) = 0


1
t<0
t=0
t>0
rampa(t) =
Note que rampa(t) =
Rt
−∞
(
u(τ )dτ = tu(t).
1.5 Sinal Unitário
Define-se o sinal sgn(t) como
Note que sgn(t) = 2u(t) − 1.
ET75H - SINAIS E SISTEMAS 1 - 2sem13
Prof.: Rafael Souto - Aula 02
1.6 Pulso Retangular Unitário
Define-se o sinal rect(t) como
rect(t) =
Note que rect(t) = u(t + 21 ) − u(t − 12 ).


1
|t| <
|t| =
|t| >
1
2


0
1
2
1
2
1
2
1.7 Pulso Triangular Unitário
Define-se o sinal ∆(t) como
∆(t) =
(
1 − |t|
0
|t| < 1
|t| ≥ 1
1.8 Sinc Unitário
Define-se o sinal sinc(t) como
sinc(t) =
sen(t)
t
Trata-se de um sinal utilizado para representar matematicamente a reconstrução de sinais contínuos
a partir de sinais discretos. Note que esse sinal não possui uma descontinuidade em t = 0, pois
limt→0 sen(t)
= 1.
t
2 Relações entre Sinais
2.1 Operações envolvendo sinais
• As operações básicas (adição, subtração, multiplicação e divisão) são realizadas ponto a ponto.
• Multiplicação por escalar (amplificação, atenuação, reflexão): y(t) = ax(t),
a = fator de ganho.
• Diferenciação: y(t) = dtd x(t).
Rt
• Integração: y(t) = −∞ x(τ )dτ .
2.2 Principais transformações da variável independente
• Deslocamento para a direita: y(t) = x(t − t0 ).
• Deslocamento para a esquerda: y(t) = x(t + t0 ).
• Reversão no tempo: y(t) = x(−t).
• Contração no tempo: y(t) = x(at),
|a| > 1.
• Expansão no tempo: y(t) = x(at),
|a| < 1.
OBS: A ordem em que as transformações são aplicadas importa para a composição do sinal resultante.
Note que
v(t) = x(t + b) e y(t) = v(at)
mas v(t) = x(at) e y(t) = v(t + b)
⇒
⇒
y(t) = x(at + b),
y(t) = x(at + ab).