Antiga Física Quântica

Antiga Física Quântica 2010
Antiga Física Quântica
Notas de aulas (rascunho)
Introdução
Capítulo 1. Radiação térmica e o Corpo Negro
Secção 1.1 - O corpo Negro
Secção 1.2 – Teoria clássica da Radiação de Cavidade de Rayleigh – Jeans
Secção 1.3 – Teoria de Planck da Radiação de Cavidade
Introdução
O início do século XX foi marcado pelas grandes descobertas da física
contemporânea. A física clássica tornou-se limitada do ponto de vista de suas
aplicações.
Na primeira década do século XX surgiu a teoria da relatividade especial
e o início da teoria quântica. O problema envolve velocidades muito grandes
no primeiro caso, e corpos de dimensões extremamente pequenas no
segundo.
O objetivo aqui é a apresentação de tratamentos elementares das
propriedades de quase todos os sistemas quânticos. Para isso, inicialmente
abordaremos uma introdução dos vários fenômenos do inicio da física
quântica e desenvolveremos as idéias essências da dita antiga teoria quântica.
Em seguida, veremos os fundamentos da Mecânica Quântica e as aplicações a
átomos monoeletrônicos e polieletrônicos.
O nível desta abordagem de física quântica é intermediário entre os de
física básica e um rigoroso de Mecânica Quântica. Vários detalhes matemáticos
serão omitidos para que os conceitos físicos sejam enfatizados.
Capítulo 1 – Radiação Térmica e Corpo negro
Um trabalho apresentado por Max Planck (1858-1947) em 14 de
dezembro de 1900 de título “Sobre a Teoria da lei de Distribuição de Energia
do Espectro Normal”, onde as concepções clássicas não estavam sendo
verificadas, marcou um início de uma revolução na física. Esta data é
considerada como sendo a do nascimento da física quântica. A física quântica
não substitui a clássica, mas representa uma generalização, que inclui as leis
clássicas como casos especiais.
1
Antiga Física Quântica 2010
A radiação emitida por corpos aquecidos é denominada radiação
térmica. A matéria em estado condensado (isto é, sólido ou líquido) emite um
espectro contínuo de radiação. À temperatura normal, um corpo pode ser visto
não por emissão, mas por reflexão de luz. No entanto à temperaturas altas os
corpos podem emitir luz própria, embora mais de 90% esteja na região do
infravermelho do espectro eletromagnético. Exemplos de corpos que radiam
no visível são carvão em brasa, filamento de lâmpadas e estrelas. A relação
entre a temperatura de um corpo e a freqüência, ou cor, que emitem pode ser
utilizada como um espectrômetro, conhecido como pirômetro óptico. Com um
instrumento como este é possível estimar a temperatura de um corpo
aquecido, como por exemplo, uma estrela distante, observando simplesmente
a cor, ou distribuição de freqüência, da radiação térmica por ela emitida.
Secção 1.1 – O Corpo Negro
Em geral, o espectro da radiação térmica emitido por um corpo
aquecido depende da sua composição. Entretanto, a experiência mostra que é
possível idealizar um corpo aquecido que emite espectro térmico de caráter
universal. Trata-se do chamado “corpo negro” que são corpos cuja superfície
absorve toda a radiação térmica incidente sobre ela. Todos os corpos negros, à
mesma temperatura, emitem radiação térmica de mesmo espectro.
Um corpo negro pode ser representado convenientemente por uma
cavidade, dotada de um pequeno orifício, como mostra a fig. (1.1).
Praticamente, toda a radiação vinda do exterior que passa pelo orifício, entra
na cavidade, dificilmente consegue sair dela, e termina por ser absorvida.
Assim esse orifício se comporta como um corpo negro.
Fig. (1.1) – Cavidade com um pequeno orifício que se comporta como
um corpo negro.
O parâmetro utilizado para descrever a distribuição espectral da
radiância de um corpo negro, a uma temperatura absoluta T é a radiância RT,
2
Antiga Física Quântica 2010
que se refere a energia total radiada pelo objeto por unidade de área e tempo,
definida por,
∞
RT = ∫0
RT (𝜈) 𝑑𝜈 (1.1)
onde, RT (𝜈) é a radiância por unidade de intervalo de freqüência 𝑑𝜈,
denominada de radiância espectral, e dá a distribuição de radiância de um
corpo negro, definida de forma que, RT (𝜈) 𝑑𝜈 seja a energia emitida por
unidade de área e tempo com freqüências no intervalo entre 𝜈 e 𝜈 + 𝑑𝜈.
Em 1879, Josef Stefan (1835-1893) usando argumentos empíricos,
demonstrados teoricamente mais tarde por Ludwig Boltzmann (1844-1906),
propõe que a radiação seja proporcional a quarta potência de temperatura, isto
é,
RT = 𝜎 T4 (1.2)
onde, 𝜎 = 5,67 x 10-8 w/ m² . k4 é chamada de constante de StefanBoltzmann, e a equação (1.2) é conhecida como lei de Stefan- Boltzmann.
A fig. (1.2) mostra a radiância espectral RT (𝜈) de um corpo negro para
diferentes temperaturas, obtida experimentalmente por O. R. Lummer (18601925) e, E. Prungshein (1859-1917) em 1899.
Fig. (1.2) – Radiância espectral de um corpo negro em função da
freqüência e temperatura.
A fig.(1.2) mostra que o espectro se desloca para as freqüências
máximas 𝜈máx à medida que a temperatura aumenta. Este comportamento é
linear, isto é,
3
Antiga Física Quântica 2010
𝜈máx ∝ T (1.3)
e já tinha sido demonstrado por Wilhelm Wien (1864-1928) em 1893, usando
argumentos de termodinâmica, e por isso ficou conhecido como lei do
deslocamento de Wien.
A distribuição espectral da radiação de um corpo negro pode ser
eventualmente descrita em termos de comprimentos de onda 𝜆.
A radiância RT na equação (1.1) pode ser escrita nas duas formas
seguintes:
∞
RT = ∫0
∞
RT (𝜈) 𝑑𝜈 =
∫0
RT (𝜆) 𝑑𝜆 (1.4)
A segunda integral RT (𝜆) descreve a radiação espectral distribuída em
comprimentos de onda. Podemos transformar uma integração sobre 𝜈 em uma
integração sobre 𝜆, utilizando-se a seguinte regra:
∞
RT = ∫0
0
𝑑𝜈
𝑑𝜆
RT (𝜈) 𝑑(𝜈) = ∫∞ RT (𝜈)
∞
𝑑𝜆= - ∫0
RT (𝜈)
𝑑𝜈
𝑑
𝑑𝜆
(𝜆) (1.5)
Note que os limites de integração é invertido para acomodar a relação
inversa entre 𝜈 e 𝜆, dada por,
𝜈=
𝑐
𝜆
(1.6)
Comparando-se as últimas integrais das equações (1.4) e (1.5), e
𝑑𝜈
−𝑐
notando que da equação (1.6), 𝑑𝜆 = 𝜆² , obtemos:
RT (𝜆) = - RT (𝜈)
𝑑𝜈
𝑑𝜆
=
𝑐
𝜆²
RT (𝜈) (1.7)
Note que a dependência de RT (𝜆) com 𝜆, não é o mesmo que a
dependência de RT (𝜈) com 𝜈. Em particular a lei do deslocamento de Wien,
pode ser reescrita, utilizando-se 𝜈máx = c/𝜆máx, como:
𝜆máx ∝
1
𝑇
(1.8)
ou seja, agora os valores de 𝜆 para máximos de radiância, diminuem com o
aumento da temperatura. A constante de proporcionalidade na equação (1.8),
conhecida como constante de Wien, foi determinada empiricamente e vale,
4
Antiga Física Quântica 2010
λmáx T = 2, 898 x 10-3 m . k (1.9)
Exemplo 1.1
Supondo-se que as superfícies das estrelas se comportem como corpos
negros, pode-se obter uma boa estimativa de suas temperaturas medindo-se
𝜆máx. Para o Sol, 𝜆máx = 5100 Å, enquanto que para a estrela do norte (Estrela
Polar) 𝜆máx = 3500 Å.
(a) Achar a temperatura da superfície dessas estrelas e, (b) determinar a
radiância dessas estrelas.
Solução
(a) De acordo com a lei de deslocamento de Wien,
λmáx T = 2, 898 x 10-3 m . k
Para o Sol, λmáx = 5100 Å = 5,1 x 10-7 m , logo,
5,1 x 10-7. T = 2, 898 x 10-3 ⇒ T = 5700 k
Para a estrela polar, λmáx = 3500 Å = 3,5 x 10-7 m, logo,
3,5 x 10-7 . T = 2,898 x 10-3
⇒ T = 8300 k
Observe que, pelo fato da Estrela Polar emitir mais no ultravioleta, ela é
mais quente do que o Sol. O Sol emite mais intensamente na região visível do
espectro, sugerindo que, durante a evolução humana, nossos olhos tornaramse mais sensíveis aos comprimentos de onda desta região do espectro.
(b) Pela lei de Stefan–Boltzman, RT = 𝜎 T4, assim,
Para o Sol,
RT = 5,67 x 10 x 10-8 x (5700)4
⇒ RT = 5,9 x 107 w/m2
ou,
RT ≅ 6000 w/cm2
Para a Estrela do Norte,
RT = 5, 67 x 10-8 x (8300)4
ou,
5
⇒ RT = 2,71 x 108 w/m2
Antiga Física Quântica 2010
RT ≅ 27000 w/cm2
Secção 1.2 – Teoria clássica da Radiação de Cavidade de Rayleigh – Jeans
No início do século XX, John Rayleigh (1842-1919) e James Jeans (18771946), utilizaram a teoria clássica para estudar a densidade de energia da
radiação de cavidade, ou de corpo negro, que resultou em sérias divergências
com resultados experimentais. Estas divergências revelam-se como uns dos
fatos históricos mais importantes para o nascimento da teoria quântica. Nesta
secção, vamos apresentar os cálculos feitos por Rayleigh e Jeans e discutir as
divergências observadas. Na secção seguinte, discutiremos a teoria de Planck
para a radiação de cavidade, que introduziu a quantização da energia.
Se
as
paredes
internas
da
cavidade
da
fig.(1.1),
estiverem
uniformemente aquecidas a uma temperatura T, o orifício atua como um
emissor de radiação, como mostra a fig. (1.3).
Fig. 1.3 – cavidade uniformemente aquecida emissora de radiação
Como o orifício tem propriedade de uma superfície de corpo negro, a
radiação emitida por ele deve também ter um espectro de Corpo Negro. O
espectro emitido pelo orifício na cavidade será especificado também por uma
radiância espectral RT (𝜈). No entanto, é mais útil, especificar o espectro da
radiação dentro da cavidade, conhecida como radiação de cavidade, em termos
de uma densidade de energia ϱT (𝜈). Evidentemente, essas quantidades são
proporcionais entre si.
A relação entre a radiância RT e a densidade de energia 𝜚T, pode ser
encontrada com a ajuda de uma esfera imaginária com o orifício da cavidade
em sua superfície, como mostra a fig.(1.4).
6
Antiga Física Quântica 2010
Fig.(1.4) – Esfera imaginária com orifício da cavidade.
Devemos notar que, como somente um dos hemisférios 𝑑𝐴 contém o
orifício, então num intervalo de tempo ∆t, a energia radiada ∆ER será metade da
energia ∆EC da cavidade. Além disso, somente radiação com cavidade <cZ>
atravessam o furo. Evidentemente, a média <cZ> pode ser ponderada em
𝜋 𝜋
qualquer intervalo do hemisfério [ - , ]. Em particular, pode-se ponderá-la
2
𝜋
2
no octante [0, 2 ]. Com essas considerações, obtém-se:
RT =
∆𝐸𝑐
∆𝑡
.
1
∆𝑡
.
<∆𝑧>
<∆𝑧>
=
1
2
<cZ>
∆𝐸𝑐
∆𝑉
=
1
2
<cZ> 𝜚T
com, <cZ> ponderada na área da semi- esfera:
<cZ> =
𝜋/2
∫0
(𝑥 𝑐𝑜𝑠𝜃)2𝜋𝑟² 𝑠𝑒𝑛𝜃 𝑑𝜃
𝜋/2
∫0
2𝜋𝑟² 𝑠𝑒𝑛 𝜃 𝑑𝜃
=
0
2𝜋𝑟² 𝑐 ∫1 𝑥 𝑑 𝑥
2𝜋𝑟²
0
∫1 𝑑𝑥
=
𝑐
2
onde, adotou-se a mudança de variável 𝑥 = 𝑐𝑜𝑠 𝜃. Assim, a radiância e a
densidade de energia na cavidade se relacionam por,
RT =
𝑐
4
𝜚T
ou, num intervalo de freqüências entre 𝜈 e 𝜈 + 𝑑𝜈,
RT (𝜈)𝑑𝜈 =
𝑐
4
𝜚T (𝜈) 𝑑𝜈 (1.10)
ou ainda, em termos de comprimento de onda,
RT (𝜆) 𝑑𝜆 =
7
𝑐
4
𝜚T (𝜆) 𝑑𝜆 (1.11)
Antiga Física Quântica 2010
pois, como c = 𝜆𝜈 ,
𝑑𝜈
𝑑𝜆
=
−𝑐
𝜆²
, e portanto 𝑑𝜈 é proporcional a – 𝑑𝜆 . Pode-se
considerar as paredes internas da cavidade perfeitamente condutra, tal que, os
campos sejam confinados, e que a energia seja armazenada na forma de ondas
eletromagnéticas estacionárias de modos discretos para qualquer freqüência 𝜈.
Podemos então, determinar a densidade de energia espectral 𝜚T (𝜈) 𝑑(𝜈) num
intervalo de freqüência entre 𝜈 e 𝜈 + 𝑑 (𝜈), simplesmente contando o número
de modos 𝑁 (𝜈) 𝑑𝜈 no mesmo intervalo de freqüências e multiplicando pela
energia total média < ℇ > de cada modo:
ϱT (𝜈) 𝑑(𝜈) =
𝑁(𝜈)𝑑(𝜈)
𝑉
< ℇ > (1.12)
onde, V é o volume da cavidade. O problema se reduz então na determinação
dos fatores 𝑁 (𝜈) 𝑑(𝜈) e < ℇ >.
Para
simplificação
matemática
na
determinação
de
𝑁(𝜈) 𝑑(𝜈),
assumiremos que a forma da cavidade seja cúbica de dimensões L, como
mostra a fig.(1.5). Nesse caso, as componentes dos campos elétricos 𝐸⃗ e
⃗ , podem ser tratadas separadamente, por causa do paralelismo
magnético 𝐵
das paredes.
Fig.(1.5) – Cavidade cúbica perfeitamente condutora.
A radiação eletromagnética é uma vibração transversal, com vetores 𝐸⃗ e
⃗ perpendiculares à direção de propagação como também mostrado na
𝐵
fig.(1.5).
⃗ é obtido
O comportamento espacial e temporal dos campos ⃗⃗⃗
𝐸 e 𝐵
através das equações de J. C. Maxwell (1871-1879). Entretanto, por causa da
natureza vetorial desses campos, o tratamento matemático envolvido na
solução geral do problema é bastante tedioso. Ao invés de fazê-lo, vamos
optar inicialmente, por resolver uma situação hipotética simplificada, onde a
cavidade seja unidimensional de comprimento L, de modo que a natureza
vetorial dos campos possam ser ignoradas. Uma vez resolvido este problema
8
Antiga Física Quântica 2010
simples, vamos generalizá-lo ao caso tridimensional utilizando argumentos
geométricos simples.
Ao longo do eixo-x, os campos E (x, t) e B (x, t), satisfazem a equação
de onda semelhantes ao caso de cordas vibrantes presas pelas extremidades,
isto é,
𝜕² 𝐸(𝑥,𝑡)
𝜕𝑥²
=
1 𝜕² 𝐸(𝑥,𝑡)
𝑐²
𝜕𝑡²
(1.13)
e uma equação similar para B (x,t); que não será explicitada aqui. Nesta
equação 𝑐 = 𝜆𝜈, é a velocidade da luz (c = 3,00 x 108 m/s). A solução da
equação (1.14) para uma onda estacionária (resultante da soma de onda para
direita e esquerda), será:
E (x,t) = E0 [sen (kx + wt) + sen (kx - wt)] = E0 sen kx sen wt (1.14)
onde,
2𝜋
𝜆
k=
e, w = 2𝜋𝜈 (1.15)
são, respectivamente, o numero de ondas e a freqüência angular. A identidade
na equação (1.14) pode ser verificada usando-se a relação, sen 𝛼 + sen 𝛽 = 2
1
1
sen 2 (𝛼 + 𝛽) cos 2 (𝛼 − 𝛽).
A equação (1.14), descreve o comportamento de uma onda cuja
amplitude varia senoidalmente, no espaço e no tempo, ao longo do eixo-x e
com freqüência 𝜈. Esse comportamento deve ser espacialmente localizado,
como ondas estacionárias, exibindo nódos em 𝑥 = 0 e 𝑥 = L. Para que o
campo E (x, t) seja nulo nesses pontos, de acordo com a equação (1.14), sen
(2𝜋𝐿/𝜆) = 0, ou 2𝜋𝐿/𝜆 = 𝑛𝜋 onde, n = 0, 1, 2,..., ou seja, o comprimento de
onda λ deve assumir valores dados por,
λ=
2𝐿
𝑛
; n = 0, 1, 2, ... (1.16)
ou ainda, em termos de freqüência,
𝜈=
9
𝑐
𝜆
=
𝑐
2𝐿
n; n = 0, 1, 2,... (1.17)
Antiga Física Quântica 2010
Esta condição determina um conjunto de valores possíveis de comprimentos
de onda, ou freqüências, que devem se propagar na cavidade unidimensional.
A figura (1.16) mostra ondas estacionárias para n = 1, 2, 3.
Fig.(1.6) – Ondas estacionárias para n = 1, 2 e 3.
Um comportamento similar se obtêm quando se considera as dimensões y e z
individualmente, isto é, as radiações se propagam de modo que suas três
componentes espaciais são ondas estacionárias.
Para generalizar o problema ao caso tridimensional, consideremos uma
radiação de comprimento de onda λ, propagando-se numa direção definida
pelos três ângulos diretores 𝛼, 𝛽 𝑒 𝛾, como mostra a figura (1.7). Obviamente,
as radiações devem ser ondas estacionárias já que suas componentes espaciais
o são e, neste caso, os nódos são planos distanciados de 𝜆/ 2.
Fig.(1.7) – Planos nodais que se propagam numa certa direção na cavidade
cúbica.
Como na equação (1.16) os comprimentos de onda associados a cada
coordenada espacial, serão,
10
Antiga Física Quântica 2010
λx = 2L/ nx; λy = 2L/ ny ; λz = 2L/ nz (1.18)
onde, nx , ny , nz = 0, 1, 2, ... . Estas componentes podem ser escritas em
termos do comprimento de onda λ, como sugere a figura (1.7),
cos 𝛼 = λ/ λx ; cos 𝛽 = λ/ λy ; cos 𝛾 = λ/ λz (1.19)
que relacionadas com as equações (1.18), fornecem,
2𝐿
𝜆
cos 𝛼 = nx ;
2𝐿
𝜆
cos 𝛽 = ny ;
2𝐿
𝜆
cos 𝛾 = nz
Elevando-se ambos os membros destas equações ao quadrado e, em seguida
somando-os, obtemos
2𝐿
𝜆
( )² (cos² 𝛼 + cos² 𝛽 + cos² 𝛾 ) = nx² + ny² + nz²
O segundo termo entre parênteses, define a soma dos co-senos diretores dada
por,
cos² 𝛼 + cos² 𝛽 + cos² 𝛾 = 1 (1.20)
e, então,
2𝐿
𝜆
= (nx² + ny² + nz²)1/2; nx, ny, nz = 0, 1, 2, ... (1.21)
Em termos de freqüência, a equação (1.21) pode ser escrita como,
ν =
𝑐
𝜆
=
𝑐
2𝐿
(nx² + ny²+ nz²) ; nz , ny , nz = 0, 1, 2, ... (1.22)
Essas equações descrevem novamente um conjunto de valores possíveis de
comprimento de onda e freqüência, agora para o caso geral da cavidade cúbica
condutora.
Vamos agora contar o número de modos 𝑁 (𝜈) 𝑑𝜈, no intervalo de
freqüência entre 𝜈 e 𝜈 + 𝑑𝜈, construindo uma esfera de raio
r = (nx² + ny² + nz²)1/2 (1.23)
11
Antiga Física Quântica 2010
em coordenadas retangulares, tal que o conjunto de inteiros nx , ny
e nz
definem pontos no interior de um octante do sistema de coordenadas, fig.
(1.8).
Fig.(1.8) – Espaço (nx, ny , nz ) definindo um octante esférico de raio r =
(nx² + ny² + nz²)1/2.
O volume total do octante esférico pode ser dividido em volumes unitários,
contendo cada um, apenas um ponto (nx, ny , nz). Esta construção permite
definir a densidade de pontos como,
ϱ = 1 ponto/ unidade de volume (1.24)
Cada ponto (nx, ny, nz ) corresponde a uma freqüência possível 𝜈, que se
relaciona ao raio r, de acordo com as equações (1.22) e (1.23), como
r=
2𝐿
𝑐
𝜈 (1.25)
Assim, calcular o número de modos N (𝜈)𝑑𝜈 entre 𝜈 e 𝜈 + 𝑑 𝜈, é equivalente a
calcular o número de pontos N (𝑟) 𝑑𝑟, contidos entre as cascas esféricas entre 𝑟
e 𝑟 + 𝑑𝑟. O valor de N (𝑟) 𝑑𝑟 pode ser calculado simplesmente, multiplicando o
volume da camada entre 𝑟 e 𝑟 + 𝑑𝑟 pela densidade de pontos, isto é,
1
1
𝑁 (𝜈) 𝑑𝜈 = 𝑁 (𝑟) 𝑑𝑟 = (8 4πr²) 𝑑𝑟 𝜚 = 2 πr² 𝑑𝑟
pois,
𝜚 = 1. Utilizando a equação (1.25) e sua derivada, 𝑑𝑟 = (2𝐿/𝑐) 𝑑𝜈, na
equação anterior obtém-se:
𝑁 (𝜈) 𝑑𝜈 = ½ π (
2𝐿
𝑐
𝜈)² (
2𝐿
)
𝑐
𝑑𝜈 =
4𝜋𝜈²
𝑐³
onde, usamos o volume da cavidade como, V = L³.
12
V 𝑑𝜈 (1.26)
Antiga Física Quântica 2010
Finalmente, devemos multiplicar o resultado da equação (1.26) por um fator 2,
pois, para cada freqüência possível 𝜈, há, na verdade, duas ondas
independentes correspondentes aos dois possíveis estados de polarização da
radiação eletromagnética, que podem estar ou não em fase, isto é,
𝑁 (𝜈) 𝑑𝜈 =
8𝜋𝑉
𝑐³
𝜈² 𝑑𝜈 (1.27)
Apesar de nossos cálculos terem sido feitos para uma cavidade, pode-se
mostrar que N (𝜈) depende apenas do volume da cavidade e não de sua forma.
Relacionando-se a equação (1.27) com a equação (1.12), obtém-se:
ϱT (𝜈) 𝑑𝜈 =
8𝜋𝜈²
𝑐³
< ℇ > 𝑑𝜈 (1.28)
Classicamente, as ondas estacionárias de freqüência 𝜈 são geradas por
oscilações de partículas carregadas das paredes da cavidade, como se fossem
pequenos corpos presos a molas, mantidos em equilíbrio térmico a uma
temperatura T.
Baseando-se no modelo clássico da teoria cinética dos gases, na qual
um sistema de moléculas em equilíbrio térmico a uma temperatura T, o
princípio da eqüipartição da energia, afirma que a energia cinética média de
uma molécula por grau de liberdade é,
1
2
𝐾𝑇
onde, 𝐾 = 1,38 𝑥10 − 23 𝐽/ 𝑘, é a constante de Boltzmann.
Podemos aplicar este princípio à partículas oscilantes das paredes da cavidade
desde que consideremos também a energia potencial dessas partículas. No
equilíbrio térmico, em média, as contribuições da energia cinética e potencial
1
para a energia total, são iguais a 𝐾𝑇. Logo, nessas condições, a energia total
2
média será 𝐾𝑇. No nosso caso, as ondas estacionárias tem somente um grau
de liberdade dada pela direção da oscilação das partículas, associadas ás
vibrações transversais do campo 𝐸⃗ da onda estacionária. Conclui-se, portanto,
que cada onda estacionária tem energia total média,
< ℇ > = 𝐾𝑇 (1.29)
13
Antiga Física Quântica 2010
é importante notar que a energia total média tem o mesmo valor para todas as
ondas estacionárias na cavidade, independentemente de suas freqüências.
Substituindo-se a equação (1.29) na equação (1.28), obtém-se a
densidade de energia no intervalo de freqüência entre 𝜈 e 𝜈 + 𝑑𝜈, de acordo
com previsões clássicas:
Esta relação é conhecida como a fórmula de Rayleigh-Jeans para radiação de
corpo negro.
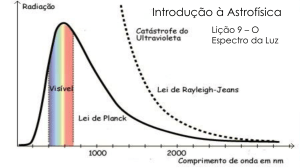
A fig.(1.9) mostra o comportamento da equação (1.30), e o resultado
experimental. A discordância é evidente. O espectro clássico se aproxima dos
resultados experimentais, somente no limite de baixas freqüências. A medida
que a freqüência cresce, o resultado teórico tende ao infinito.
Fig.(1.9) – Resultado de Rayleigh - Jeans para a radiação de um corpo negro
comparado com os resultados experimentais.
A tendência ao infinito para altas freqüências na teoria de Rayleigh - Jeans, é
conhecido como catástrofe do ultravioleta. A experiência mostra que, na
realidade, a densidade de energia vai a zero para altas freqüências.
O problema da radiação de cavidade foi resolvido por Planck, assumindo
uma hipótese sobre a eqüipartição da energia até então desconhecida. Na
secção seguinte vamos discutir essas idéias e mostrar sua importância para o
surgimento da física quântica.
1.3 – Teoria de Planck da Radiação de Cavidade
Na tentativa de solucionar a discordância entre a teoria clássica e a
experiência, para a radiação de cavidade, Planck considerou uma hipótese que
14
Antiga Física Quântica 2010
violava o princípio da eqüipartição da energia. Planck observou que o resultado
experimental seria reproduzido quando,
𝑙𝑖𝑚 < ℇ > = 𝐾𝑇 e, 𝑙𝑖𝑚 < ℇ > = 0 (1.31)
𝜈→0
𝜈→∞
isto é, a energia total média tende a KT, como na teoria clássica, quando a
freqüência tende a zero, mas tende a zero quando a freqüência tende a
infinito. Assim, Planck supõe que a energia média das ondas estacionárias seja
uma função da freqüência < ℇ > = < ℇ (𝜈) >, contradizendo o princípio da
equipartição da energia.
O princípio da equipartição da energia, tem a sua origem na distribuição
de Boltzmann, para a teoria cinética clássica. A distribuição de Boltzmann dá a
probabilidade de encontrar um sistema físico, em equilíbrio térmico a uma
temperatura T, com energia entre ℇ e ℇ + 𝑑ℇ, escrita aqui sem demonstração,
como,
P (ℇ) 𝑑ℇ =
𝑒 −ℇ/𝐾𝑇
𝐾𝑇
𝑑ℇ (1.32)
A energia média < ℇ > pode ser calculada da distribuição de Boltzmann
por,
< ℇ >=
∞
∫0 ℇ 𝑃(ℇ)𝑑ℇ
∞
∫0 𝑃(ℇ)𝑑ℇ
∞
= ∫0 ℇ 𝑃(ℇ)𝑑ℇ = ÁREA (1.33)
O denominador é a probabilidade de encontrar a entidade com qualquer
energia, sendo portanto igual a unidade. A integral na equação (1.33) pode ser
calculada utilizando a equação (1.32), e o resultado reproduz o princípio da
equipartiação da energia, isto é,
< ℇ > = 𝐾𝑇 (1.34)
A equação (1.33) mostra que < ℇ > = 𝐾𝑇 é representado pela área abaixo do
gráfico de ℇ 𝑃(ℇ) em função de ℇ, como mostra a fig. (1.10). A função ℇ P(ℇ) foi
obtida diretamente da equação (1.32). O ponto de máximo desta função
corresponde a ℇ = 𝐾𝑇 = < ℇ >.
15
Antiga Física Quântica 2010
Fig. (1.10) – Gráfico de ℇ 𝑃(ℇ) em função de ℇ.
A grande contribuição de Planck se deu quando ele descobriu que a
condição 𝑙𝑖𝑚 < ℇ > = 0, poderia ser alcançada, se fosse modificado o cálculo
de < ℇ > a partir de 𝑃(ℇ) 𝑑ℇ. Planck supôs que a energia ℇ poderia ter apenas
valores discretos, em vez de qualquer valor como utilizado na teoria clássica, e
que, os valores discretos fossem uniformemente distribuídos, isto é,
ℇ = 0, ∆ℇ, 2∆ℇ, 3∆ℇ, . .. (1.35)
Nesse caso, ∆ℇ seria o intervalo constante entre os valores discretos da
energia. Com a hipótese discreta da energia, as integrais na equação (1.33),
usadas para calcular < ℇ >, devem ser substituídas por somatórios, isto é,
<ℇ> =
∑∞
0 ℇ𝑛 𝑃(ℇ𝑛)
∑∞
0 𝑃(ℇ𝑛)
(1.36)
A fig.(1.11) mostra cálculos gráficos de < ℇ > a partir de ℇ 𝑃(ℇ) para os casos,
(a) ∆ℇ <<< 𝐾𝑇; (b) ∆ℇ ≈ 𝐾𝑇 e (c) ∆ℇ >> 𝐾𝑇.
Fig.(1.11) – Comportamento gráfico de <ℇ> de acordo com a equação (1.36).
O valor de 𝐾𝑇 será a área abaixo da curva suave. Observe que quando ∆ℇ <<<
𝐾𝑇, o valor de < ℇ > ≈ 𝐾𝑇, ou seja, praticamente igual ao resultado clássico.
Entretanto, quando < ℇ > ≈ 𝐾𝑇 ou, ∆ℇ >> 𝐾𝑇, o valor < ℇ > será menor que
𝐾𝑇, pois a redução da área definida pelos elementos discretos começa a
16
Antiga Física Quântica 2010
tornar-se evidente, quando comparamos com área definida pelos contínuos.
Conclui-se então que:
<ℇ> ≅ 𝐾𝑇 se, ∆ℇ for pequeno
e,
<ℇ> ≅ 0 se, ∆ℇ for grande
Como Pkanck precisava obter o primeiro resultado para baixas freqüência 𝜈, e
o segundo para altos valores de 𝜈, então o valor ∆ℇ deveria ser proporcional a
𝜈, isto é,
∆ℇ = ℎ𝜈 (1.37)
onde, ℎ é a constante de proporcionalidade. Cálculos posteriores permitiram a
Planck determinar o valor de ℎ, ajustando resultados teóricos com dados
experimentais, obtendo,
ℎ = 6,63 𝑥 10 − 34 𝐽. 𝑠 (1.38)
Esta constante ficou conhecida como a constante de Planck.
Vamos agora calcular a energia média utilizando a equação (1.36) e
equação (1.32), considerando nessas fórmulas a energia
ℇ = 𝑛ℎ𝜈, n = 0, 1, 2, 3, ... (1.39)
isto é,
𝑛ℎ𝜈
<ℇ>=
−
∑𝑛ℎ𝜈
𝐾𝑇 𝑒 𝐾𝑇
𝑛ℎ𝜈
1 −
∑∞
0 𝐾 𝑒 𝐾𝑇
= KT
onde,
𝛼=
podemos notar que,
−𝛼
𝑑
−𝑛𝛼
ln ∑∞
0 𝑒
𝑑𝛼
17
=
ℎ𝜈
𝐾𝑇
(1.40)
−𝑛𝛼
∑∞
0 𝑛𝛼 𝑒
−𝑛𝛼
∑∞
𝑒
0
Antiga Física Quântica 2010
de forma que,
onde usamos o valor de dado por (1.40). Mas,
onde, , de forma que,
18
Antiga Física Quântica 2010
19