Tipo A

ENG 1007 – INTRODUÇÃO À MECÂNICA DOS SÓLIDOS
Primeira prova – turma A
09/09/2014
a
1 Questão (2,5 pontos)
Calcular as reações horizontal, vertical e de
momento de engastamento da extremidade
esquerda da viga abaixo, que equilibram os
carregamentos indicados.
M =?
10 2 kN
H =?
450
4 cm
3 cm
25 kN
arctan 43
40kNm
10 cm
V =?
Resposta:
∑ FH = 0 : H = 10 + 25 × 3 5 = 25kN (para a esquerda)
∑ F = 0 : V = 10 + 25 × 4 5 = 30kN (para baixo)
∑ M = 0 : M = −40 + 10 × 0, 03 + 25 × 4 5 × 0,1 = −37, 7kNm (sentido anti-horário)
Verificação: ∑ M
= 0 : − 37, 7 − 30 × 0,1 + 10 × 0, 07 + 40 = 0
V
apoio
x =10 cm
2a Questão (2,5 pontos)
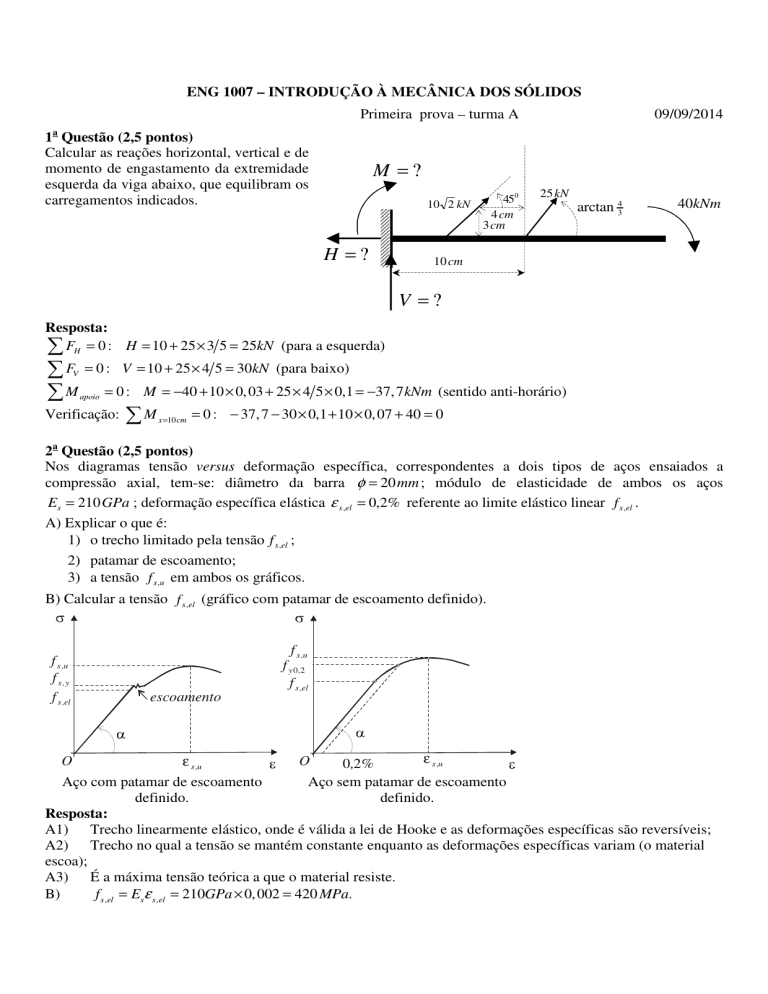
Nos diagramas tensão versus deformação específica, correspondentes a dois tipos de aços ensaiados a
compressão axial, tem-se: diâmetro da barra φ = 20 mm ; módulo de elasticidade de ambos os aços
Es = 210 GPa ; deformação específica elástica ε s ,el = 0,2% referente ao limite elástico linear f s ,el .
A) Explicar o que é:
1) o trecho limitado pela tensão f s ,el ;
2) patamar de escoamento;
3) a tensão f s ,u em ambos os gráficos.
B) Calcular a tensão f s ,el (gráfico com patamar de escoamento definido).
f s ,u
f s ,y
f s ,el
escoamento
f s ,u
f y 0,2
f s ,el
ε s ,u
O
ε s ,u
0,2%
Aço com patamar de escoamento
Aço sem patamar de escoamento
definido.
definido.
Resposta:
A1) Trecho linearmente elástico, onde é válida a lei de Hooke e as deformações específicas são reversíveis;
A2) Trecho no qual a tensão se mantém constante enquanto as deformações específicas variam (o material
escoa);
A3) É a máxima tensão teórica a que o material resiste.
B)
f s ,el = Esε s ,el = 210GPa × 0, 002 = 420 MPa.
O
3a Questão (2,5 pontos)
A barra ABCDE mostrada na Figura 4 tem dois segmentos (AB e BCDE), com diâmetros φAB = 10 cm e φBCDE
= 30 cm.
(a) Esboçar o gráfico de esforço normal, colocando apropriadamente o sinal positivo ou negativo para,
respectivamente, tração e compressão. Em seguida,
(b) determinar a tensão atuante em cada trecho da barra ABCDE.
(c) Para um módulo de elasticidade E = 210 GPa, qual será a variação de comprimento do segmento AB da
barra?
Figura 4
Resposta:
(a) Gráfico mostrado à direita
15kN
7 kN
(b) σ AB =
= 1,9099 MPa σ BC =
= 99, 03kPa
2
2
π 0,1 4 m
π 0,32 4 m2
−9kN
−5kN
σ CD =
= −127,32kPa σ DE =
= −70, 74kPa
2
2
π 0,3 4 m
π 0,32 4 m2
15kN
2, 4m
(c) δ LAB =
= 21,83 ×10−6 m
2
2
π 0,1 4 m 210GPa
4a Questão (2,5 pontos)
P
Um cilindro de borracha, de diâmetro d, é comprimido em um cilindro de aço, por uma força P (ver a figura).
Determinar a pressão p entre a borracha e o aço, para P = 5 kN, d = 5 cm e o coeficiente de Poisson da
borracha igual a 0,45.
Resposta:
Sejam z a direção axial e x e y as direções radiais (o problema é axissimétrico).
Então, os dados do problema são σ z = −4 P π d 2 , ε x = ε y = 0 . Quer-se determinar
σx =σy = ?
Pela lei de Hooke generalizada, ε x = ε y = 0 =
σx
ν
ν
σz,
E
1 −ν
ν
−4ν
−4 × 0, 45
ou seja, σ x = σ y =
σz =
P=
5kN = −2, 083MPa
2
1 −ν
(1 −ν )π d
(1 − 0, 45)π 0, 052 m2
E
−
(σ z + σ x )
⇒ σx =
d