Ficha 5 (GABARITO) - Álgebra básica

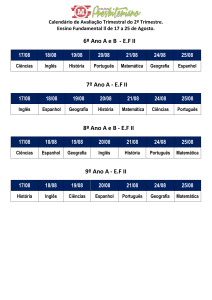
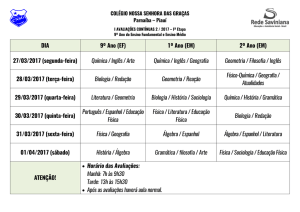
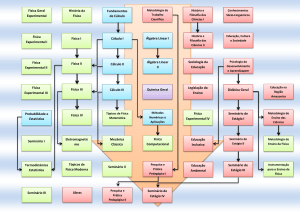
FICHA 5 – ÁLGEBRA BÁSICA
GABARITO
1)Escreva na forma de expressão algébrica cada uma das afirmações abaixo:
a) A terça parte de um número. 𝑅:
𝑥
3
b) Um número par. 𝑅: 2𝑥
c) Um número ímpar. 𝑅: 2𝑥 − 1
d) A soma de dois números consecutivos. 𝑅: 𝑥 + (𝑥 + 1)
e) A soma de um número e seu triplo. 𝑅: 𝑥 + 3𝑥
f) A soma de um número e quatro. 𝑅: 𝑥 + 4
g) O décuplo de um número. 𝑅: 10𝑥
h) O quadrado da diferença de dois números. 𝑅: (𝑥 − 𝑦)2
i) O quadrado da soma de dois números. 𝑅: (𝑥 + 𝑦)2
𝑥²
j) A sexta parte do quadrado de um número somado a dois. 𝑅: 6 + 2
k) O triplo de um número somado com o dobro de seu quadrado menos sua quinta
𝑥
parte. 𝑅: 3𝑥 + 2𝑥² − 5
l) A diferença entre um número e sete. 𝑅: 𝑥 − 7
m) O número sete diminuído de um número qualquer. 𝑅: 𝑥 − 7
n) O triplo da diferença do dobro de um número e três. 𝑅: 3(2𝑥 − 3)
o) O produto entre o quadrado de um número e o triplo de outro número. 𝑅: 𝑥². 3𝑦
2)Indique o coeficiente e a parte literal de cada um dos monômios abaixo:
a) √12. 𝑥 2 𝑦𝑧 4
Coeficiente: √12
Parte Literal: 𝑥². 𝑦. 𝑧 4
b)
5𝑥
2
5
Coeficiente: 2
Parte Literal: 𝑥
Ficha 5 – Álgebra básica
8º ano– 1º trimestre – 2016
Página 1 de 3
Disciplina: Matemática
Professora Marcia
c)− 𝑎𝑏
Coeficiente:−1
Parte Literal: 𝑎𝑏
−𝑦𝑎²𝑏
d)
5
1
Coeficiente:− 5
Parte Literal: 𝑦. 𝑎². 𝑏
3)Reduza os termos semelhantes:
a) 3a – 4b + c + 3 + 4a + 3b – 2c + 2 = 7𝑎 − 𝑏 − 𝑐 + 5
b) m²p³ – 5m³p + 4m²p³ + 3m³p – 5m²p³ = −2𝑚³𝑝
c) 3a² – 4ab + 13 + 5ab – 4a² – 5ab – 7 = −𝑎² − 4𝑎𝑏 + 6
d) d) xy² – x²y + √121 + 4xy² + 3x²y – 5 = 5𝑥𝑦² + 2𝑥²𝑦 + 6
e) e) 3a² – a² + 3a– 12a² –√𝑎² = −10𝑎² + 2𝑎
f)
𝑥²
2
−
𝑦³
3
+
𝑥²
4
−
2𝑦³
3
Ficha 5 – Álgebra básica
8º ano– 1º trimestre – 2016
3
= 𝑥² − 𝑦³
4
Página 2 de 3
Disciplina: Matemática
Professora Marcia
4) Determine o valor numérico das expressões algébricas abaixo.
a) 2a – 7b, para a = 2 e b = – 8. R: 60
b) 4y² – 6,2y + 3, para y = – 2. R: 31,4
c) 3x³y² – 5xy², para x = 2 e y = 3. R: 126
d) (a – 5).(2a – 3).(3a + 4), para a = – 2. R: - 98
e) (a² – 4ab + b²) (5a² – 3ab – 5b²), para a = – 2 e b = 3. R: - 259
3𝑥³𝑦²
f)
4
g)
𝑥³
𝑥𝑦
+
−
𝑦³
𝑥𝑧
5𝑥² 𝑦
7
+
𝑧³
𝑦𝑧
11
, para x = ½ e y = 1/3. R: − 224
, para x = – 1; y = – 2 e z = – 3. 𝑅:
1
𝑥
−
23
3
1+
5) O valor da expressão
(A) – 2/3
2−𝑥
para x = – ½ é:
(B) – 2/5
(C) 1/5
(D) 3/2
6)Sendo A = 2, B = 1 e C = 3, o valor numérico da expressão
(A) – 22/9
(B) 32/9
(C) – 2
𝐴2 − 2𝐵
3𝐶
(E) 5
𝐴
+ + 3𝐵é:
6
(D) 2
(E) 4
7)Dadas àsigualdades:
A =– a² – 2a + 5
Assinale a alternativa verdadeira:
(A)
Se a = 2 e b = – 2, então A = B
(B) Se a = – 2 e b = – 2, então A = B
(B)
e
B = b² + 2b + 5,
(D) Se a = 2 e b = 2, então A = B
(E) Se a = – 2 e b = 2, então A = B
Se a = – 2 e b = 2, então A = –B
Ficha 5 – Álgebra básica
8º ano– 1º trimestre – 2016
Página 3 de 3
Disciplina: Matemática
Professora Marcia