F128-Lista 8 1) A mola de um revólver de brinquedo tem constante

F128-Lista 8
1) A mola de um revólver de brinquedo tem constante elástica de 7,25N/cm. O revólver é inclinado de 36°
acima da horizontal e dispara uma bola de 78g à altura de 1,9m acima da boca do revólver. (a) Qual a
velocidade de saída da bola? (b) De quanto deve ter sido comprimida inicialmente a bola?
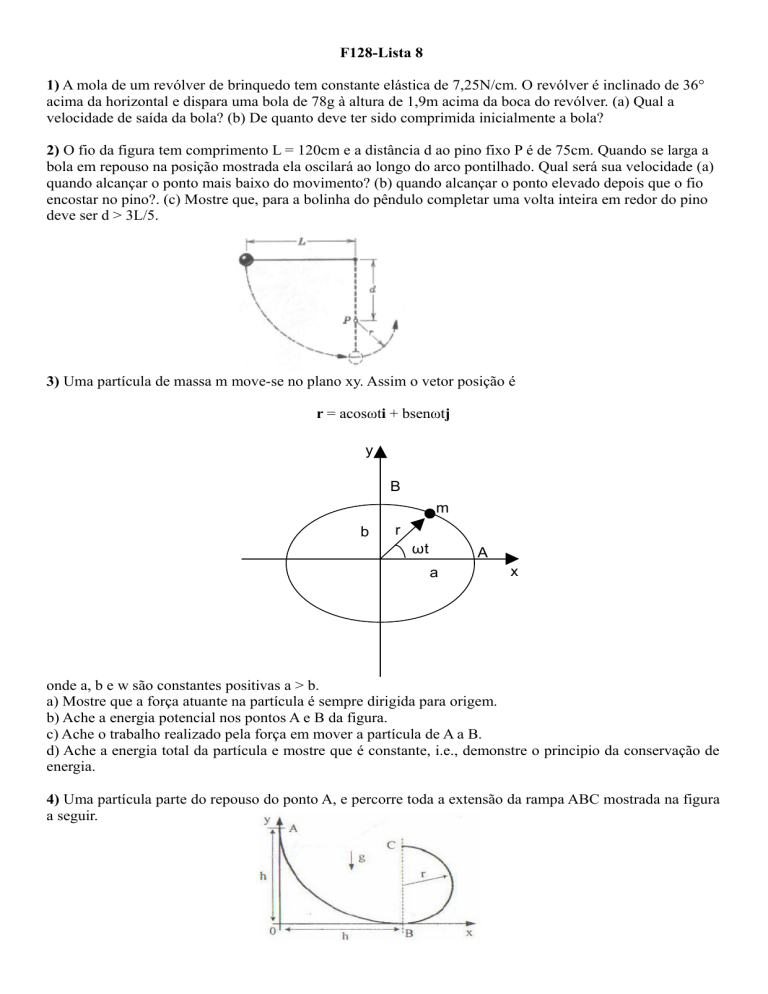
2) O fio da figura tem comprimento L = 120cm e a distância d ao pino fixo P é de 75cm. Quando se larga a
bola em repouso na posição mostrada ela oscilará ao longo do arco pontilhado. Qual será sua velocidade (a)
quando alcançar o ponto mais baixo do movimento? (b) quando alcançar o ponto elevado depois que o fio
encostar no pino?. (c) Mostre que, para a bolinha do pêndulo completar uma volta inteira em redor do pino
deve ser d > 3L/5.
3) Uma partícula de massa m move-se no plano xy. Assim o vetor posição é
r = acosωti + bsenωtj
y
B
m
b
r
ωt
A
a
x
onde a, b e w são constantes positivas a > b.
a) Mostre que a força atuante na partícula é sempre dirigida para origem.
b) Ache a energia potencial nos pontos A e B da figura.
c) Ache o trabalho realizado pela força em mover a partícula de A a B.
d) Ache a energia total da partícula e mostre que é constante, i.e., demonstre o principio da conservação de
energia.
4) Uma partícula parte do repouso do ponto A, e percorre toda a extensão da rampa ABC mostrada na figura
a seguir.
A equação que descreve a rampa entre os pontos A, de coordenadas (0,h) e B, de coordenadas (h,0), é dada
por:
x2
y=
− 2x + h
h
enquanto que entre os pontos B e C, de coordenadas (h,2r), a rampa é descrita por uma circunferência de
raio r com centro no ponto de coordenadas (h,r). Sabe-se que a altura h é a mínima necessária para que a
partícula abandone a rampa no ponto C e venha a colidir com a própria rampa em um ponto entre A e B.
Determine o ponto de colisão da partícula com a rampa no sistema de coordenadas da figura como função
apenas do comprimento r.
Dado: aceleração da gravidade = g.
OBS: despreze as forças de atrito e a resistência do ar.
5) Um pequeno corpo desliza do topo de uma montanha de altura H, cuja porção final é horizontal e que fica
a uma altura H do solo. Qual deve ser o valor de h para que a distância percorrida pelo corpo seja a maior
possível? Qual é o valor desta distância?
6) No ponto A da figura, um pequeno corpo de massa m = 0,01 kg, inicialmente em repouso, comprime uma
mola ideal de constante elástica k = 2 N/m. A compressão inicial da mola em relação à sua posição de
equilíbrio é denotada por x. Em um dado instante, a mola subitamente impulsiona o corpo, que passa a
mover-se sobre uma superfície sem atrito. Tal superfície é composta por seções retilíneas e horizontais AB e
BE, e por porções curvas BC e DB. As partes curvas da superfície são arcos de circunferência que compõem
um “loop” circular e vertical de raio R = 1 m, o qual teve a porção CD, de abertura angular 2θ = 120 0 ,
completamente retirada.
a) Calcule o valor mínimo da compressão inicial da mola para que o corpo, partindo em repouso do ponto
A, atinja o ponto E sem perder contato com a superfície ABCDE, a não ser no trecho entre C e D.
b) Nas circunstâncias do item a), calcule a força normal que o “loop” exerce sobre o corpo quando este
passa pelo ponto C. Indique claramente o módulo, a direção e o sentido do vetor.
7) Um corpo de massa m e dimensões desprezíveis é solto, a partir do repouso, do ponto A indicado na
figura a seguir. O corpo está amarrado a um fio ideal, inextensível e de massa desprezível, com
comprimento L, que encontra-se preso a um pino. Sabe-se que o fio suporta sem partir uma tensão máxima
igual a 2mg, onde g denota a aceleração da gravidade. Despreze os efeitos de atrito e resistência do ar.
a) Calcule o desnível h entre os pontos A e B, sabendo que o fio se parte no ponto B.
b) Determine as componentes horizontal e vertical da velocidade do corpo no instante em que ele atinge o
solo.
8) Uma corrente é mantida sobre uma mesa sem atrito com um quarto do seu comprimento pendurado para
fora da mesa, como na figura abaixo. S a corrente tiver um comprimento L e uma massa m, qual o trabalho
necessário para puxá-la totalmente para cima da mesa?