P1-Rosa

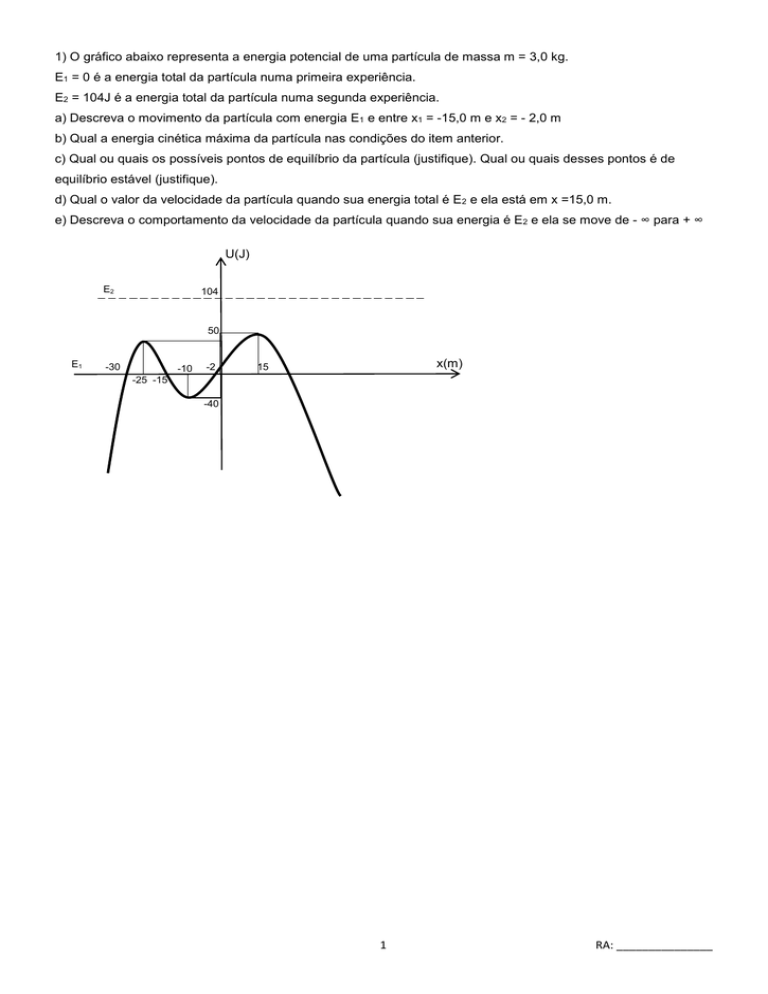
1) O gráfico abaixo representa a energia potencial de uma partícula de massa m = 3,0 kg.
E1 = 0 é a energia total da partícula numa primeira experiência.
E2 = 104J é a energia total da partícula numa segunda experiência.
a) Descreva o movimento da partícula com energia E1 e entre x1 = -15,0 m e x2 = - 2,0 m
b) Qual a energia cinética máxima da partícula nas condições do item anterior.
c) Qual ou quais os possíveis pontos de equilíbrio da partícula (justifique). Qual ou quais desses pontos é de
equilíbrio estável (justifique).
d) Qual o valor da velocidade da partícula quando sua energia total é E2 e ela está em x =15,0 m.
e) Descreva o comportamento da velocidade da partícula quando sua energia é E2 e ela se move de - ∞ para + ∞
U(J)
E2
104
50
E1
-30
-10
-2
x(m)
15
-25 -15
-40
1
RA: _______________
2) Uma partícula em movimento retilíneo no eixo x tem sua velocidade dada por:
v(x) = - Aexsenx , onde A é constante.
a) Calcule a força F(x) sobre a partícula.
b) Mostre que para x pequeno, a partícula oscila em torno de x =0 e calcule a frequência de oscilação 
2
RA: _______________
3) Uma partícula de massa m, presa uma mola de constante k, é posta a oscilar na direção x por uma força
periódica dada por:
F(t) = Fo sent
para -< t < 
com período  .
A única força de atrito sobre ela é dada por : fa= - bv, onde v é sua velocidade e b uma constante. Determine x(t)
no regime estacionário.
3
RA: _______________
4) Uma partícula de massa m ligada a um ponto fixo por uma mola é posta em movimento, a partir do repouso, por
uma força de módulo F(t) = Fo e-t na direção x e para t ≥ 0. A única força de atrito sobre ela é dada por : f a= - bv,
onde v é sua velocidade e b uma constante. Use o método de Green para determinar x(t) (para t ≥ 0).
4
RA: _______________
5
RA: _______________