Cap.VI - Unicamp

F-107
CAP.VI
Mauro M.G. de Carvalho
CAPÍTULO VI
ELETRICIDADE
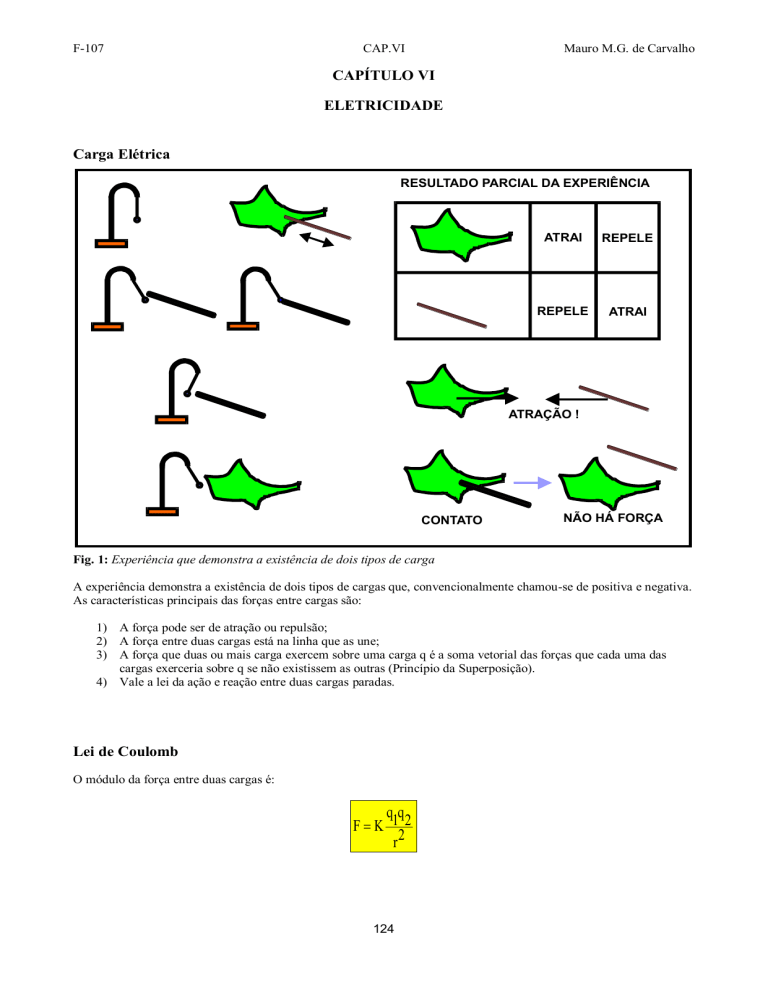
Carga Elétrica
RESULTADO PARCIAL DA EXPERIÊNCIA
ATRAI
REPELE
REPELE
ATRAI
ATRAÇÃO !
CONTATO
NÃO HÁ FORÇA
Fig. 1: Experiência que demonstra a existência de dois tipos de carga
A experiência demonstra a existência de dois tipos de cargas que, convencionalmente chamou-se de positiva e negativa.
As características principais das forças entre cargas são:
1) A força pode ser de atração ou repulsão;
2) A força entre duas cargas está na linha que as une;
3) A força que duas ou mais carga exercem sobre uma carga q é a soma vetorial das forças que cada uma das
cargas exerceria sobre q se não existissem as outras (Princípio da Superposição).
4) Vale a lei da ação e reação entre duas cargas paradas.
Lei de Coulomb
O módulo da força entre duas cargas é:
qq
FK 1 2
r2
124
F-107
CAP.VI
Mauro M.G. de Carvalho
Onde K = 9x109 u(SI), q1 e q2 são as cargas em Coulomb (C) e r a distância entre as cargas. O valor de K está ligado ao
meio e pode ser expresso como: K=1/(4o) , onde o é a permissividade elétrica do meio (8,85x10-12 u(SI) no vácuo).
-
+
+
+
+
C
+
(a)
(b)
Fig. 2: Atração e repulsão entre cargas e força (azul) na carga C (positiva) usando o princípio da superposição.
Aplic. 1: Calcule a força sobre a carga q1= 2,0C nas figuras abaixo:
a)
b)
3,0C
q1
3,0C
3,0m
1,5m
q1
d)
c)
q1
3,0C
3,0m
-2,0C
3,0C
1,0m
q1
3,0m
e)
3,0C
1,0m
f)
3,0C
3,0C
3m
q1
q1
3m
3m
3,0C
3m
3m
-3,0C
125
3m
F-107
CAP.VI
Mauro M.G. de Carvalho
Campo Elétrico: Dizemos que numa região do espaço existe um campo elétrico, quando sobre qualquer carga
elétrica nessa região atua uma força elétrica.
Intensidade de Campo elétrico: A intensidade de campo elétrico é definida como: E = F/q
A unidade de E é o N/C ou V/m.
Pela própria definição, a intensidade de campo elétrico, doravante chamada simplesmente do campo elétrico, é uma
grandeza vetorial.
Aplic. 3: Calcular o campo elétrico num ponto A distante r de uma carga q positiva. Faça uma figura para mostrar o
vetor Campo Elétrico. Repita o exercício para uma carga q negativa.
Aplic. 4: O campo elétrico numa certa região é dado por E = 100 i (V/m). Calcule o trabalho para deslocar uma carga
de 2 C (a) de (1,0) a (5,3); (b) de (3,1) a (0,0).
Aplic. 5: Na figura abaixo identificar os pontos onde o campo é mais intenso, onde ele é menos intenso e onde ele é
zero.
Diferença de Potencial (ddp): Def: VA-VB = VAB = WAB /q onde WAB é o trabalho realizado pela força elétrica
sobre a carga q para desloca-la de A até B.
Unidade de VAB é o Volt
Essa definição só é possível porque o campo elétrico é conservativo.
Aplic. 6: Mostre que o campo elétrico também pode ser medido em V/m.
Aplic.7: Na Aplicação 4, calcular a ddp A(1,0) e B(5,3) e entre C(3,1) e D(0,0).
Aplic. 8: Pode-se demonstrar que o campo entre duas placas é uniforme (exceto nas bordas) e dado, neste caso, por
/o, onde  é a densidade de carga das placas (carga por unidade de área) e o é a permissividade elétrica do meio (no
vácuo(e no ar o = 8,85x10-12 u(SI)). Duas placas metálicas iguais de 25cm2 são colocadas faca-a-face a uma distância
de 1cm. Uma ddp de 100 V é aplicada entre as placas. Qual o campo elétrico entre elas? Qual a carga em cada placa?
Aplic. 9: Um elétron é acelerado entre dois pontos entre os quais a ddp é 1000V. Considerando que inicialmente sua
velocidade era de 10m/s, calcule sua velocidade final. A massa do elétron é 9,1x10 -31 kg.
Propriedades específicas dos condutores
O campo eletrostático dentro de um condutor é zero.
O potencial elétrico dentro de um condutor é constante, logo a ddp entre dois pontos no seu interior é zero.
Capacitores: São armazenadores de energia.
Símbolo:
As cargas nas placas dos capacitores são sempre iguais e de sinais opostos. O campo elétrico no seu interior é : E = /
onde  é a permissividade do meio. A razão k = o é chamada constante dielétrica do meio.
Capacitância: A capacitância de um capacitor é definida por: C = Q/V
Onde Q é a carga na placa positiva do capacitor e V a diferença de potencial entre suas placas.
A unidade de C é o Farad (F).
126
F-107
CAP.VI
Mauro M.G. de Carvalho
Aplic. 10: Calcule a capacitância de uma capacitor de capacitor cujas placas têm área A , distam d entre si e tem um
dielétrico de constante k entre as palcas..
Aplic. 11: Aplica-se uma tensão de 100V num capacitor de 20F. Qual a carga no Capacitor.
Aplic. 12: Quando um capacitor está carregado, a energia nele armazenada é dada por U= CV 2/2. Calcule a energia
armazenada no capacitor do exercício acima.
Aplic. 13: Considere um capacitor carregado e duas lâmpadas, uma de 20W e outra de 100W. Ao se ligar a lâmpada de
100W no capacitor, ela acende e apaga logo depois. Explique o porquê desse comportamento. O que aconteceria se a
lâmpada ligada fosse a de 20W?
Corrente elétrica
i = dq/dt
ou, no caso em que i é constante , i = q/t
Unidade: A unidade de i é Coulomb/segundo que é chamada Ampère (A).
Para haver corrente é necessário haver:
1) Cargas livres (ou quase).
2) Um Campo elétrico (ou, o que vem a ser a mesma coisa, uma ddp).
Resistência eletrica : É a resistência que um condutor opõe à passagem de corrente elétrica. É dada pela razão entre a
ddp e a corrente no condutor.
R = V/i (volt/Ampère)
A unidade de R é o Ohm ()
Lei de Ohm: É constante a resistência de um condutor, ou seja, se aumentamos a ddp nos terminais de um condutor,
a corrente também aumenta de modo que V/i se mantem constante.
A resistência elétrica de um material é diretamente proporcional a seu comprimento (L) e às suas características
intrínsecas e inversamente proporcional à área de sua seção reta (A).
R  ρ
L
A
 é a resistividade do material e é medido em Ohm-m ou Ohm-cm. O inverso da resistividade é a condutividade que é
medida em Ohm-1-cm-1 .
Resistor : É um elemento passivo cuja função é dissipar energia elétrica. Símbolo:
Aplic. 14: Determine a ddp num resistor de 100k percorrido por uma corrente de 1mA
Aplic. 15: Calcule a ddp nos resistores da figura abaixo one VAB = 120V.
A
B
2
8
Gerador: É um elemento que transforma algum tipo de energia em energia elétrica. Símbolo
-
+
Força Eletromotriz (FEM): É a energia por unidade de carga que um gerador fornece às cargas. E = W/q
A unidade de FEM é o Volt.
Os geradores têm uma resistência interna que dissipa parte da energia que é obtida da sua fonte de energia. A potência
útil de um gerador é, portanto: Pu = Pf - Pp, onde Pu é a potência útil que um gerador pode fornecer, Pf é a potência
fornecida pelo sua fonte de energia (química, mecânica, solar etc) e Pp é a energia dissipada no gerador (internamente).
Energia e potência elétrica
Se V é a ddp entre dois pontos, então, pela própria definição de V , W = qV., mas sendo q = it, temos:
W = V.i t
127
F-107
Evidentemente, a potência será:
CAP.VI
Mauro M.G. de Carvalho
P = Vi
Aplic. 16: Num gerador a ddp entre seu terminal positivo e negativo é 10V quando a corrente é 10A. Qual sua potência
útil.
Aplic. 17: Mostre que a potência dissipada numa resistência pode ser dada por : P = Vi = Ri 2 = V2/R
Aplic. 18: Se a resistência interna da bateria da aplicação 16 é 0,20, qual sua FEM?
Aplic. 19: Qual a resistência de uma lâmpada de 60W-120V?
Aplic. 20: Qual a corrente num chuveiro elétrico de 2200W-220V?
Aplic. 21: Se você tem que escolher entre um chuveiro elétrico de 2200W-120V e outro de 2200W-220V, qual
escolheria (após o curso de F-107, claro!).
128
F-107
CAP.VI
Mauro M.G. de Carvalho
Magnetismo
Existem dois pólos - norte e sul - que não podem existir separadamente. A divisão de um imã gera outros imãs sempre
com os dois pólos
S
S
N
S N
D
S N
D
S N
DD
N
S
N
Figura 3 – Imãs divididos continuam imãs com dois pólos
S N
D
O magnetismo pode estar naturalmente presente em materiais tipo magnetita e ferro. Mas ele pode ser obtido através de
corrente elétrica o que gera um grande número de aplicações.
A passagem de uma corrente elétrica num fio faz aparecer um campo magnético perpendicular ao fio. Isso pode ser
constatado pelo movimento de uma agulha magnética colocada sobre o fio, conforme mostra afigura ao lado.
Sem corrente
Figura 4 - Desvio da agulha magnética devido à corrente no
fio.
i
O fio também sofre ação do campo
magnético como pode ser constatado
com a experiência mostrada na figura
Figura 5 – O condutor sobe quando é
colocado num campo magnético
demonstrando que aparece uma forçca
na corrente devido ao campo magnético
F
129
F-107
CAP.VI
S
Mauro M.G. de Carvalho
v
N
Figura 6 – O imã em movimento faz aparecer uma corrente na espira circular.
Força sobre carga em campo magnético
Características:
B
V

F
1. Força magnética só se manifesta em cargas em movimento;
2. A força magnética é perpendicular à velocidade da carga e ao campo magnético (ou
seja, ao plano formado por v e B). Portanto, a força magnética não muda o módulo da
velocidade ou, em outras palavras, não muda a energia cinética da carga.
3. O módulo da força magnética vale F= qvBsenPortanto, se a velocidade tem a
mesma direção do campo, a força magnética é nula.
Matematicamente podemos escrever: F = q(vxB). O sinal "x" aqui significa produto
vetorial.
Figura 7 – Os três vetores v,B e F.
Regra da mão direita:
Esta é uma regra útil para determinar a direção
de um dos três vetores (v, B ou F) conhecendo
os outros dois.
Figura 8 – A posição da mão direita representando v B e F
Num plano, se uma força é sempre normal à velocidade o movimento é circular uniforme. Portanto, se uma partícula
carregada entra numa região de campo magnético uniforme e perpendicular a sua velocidade, seu movimento será
circular e uniforme. Vejamos algumas propriedades desse movimento.
130
F-107
CAP.VI
Mauro M.G. de Carvalho
Partícula carregada em campo magnético uniforme
A força que faz a partícula girar é a força centrípeta que, no caso é a força magnética
Fc = FM
onde Fc = m v2/R e FM = qvB sen90o
, logo:
mv2/R = qvB
R = mv/qB
Observe que mv é o momento da partícula, ou seja, p = mv. Logo,
podemos escrever:
R = p/qB
R
Se expressarmos a energia cinética da partícula em função do
momento, o raio da trajetória poderá ser dado em função da energia
cinética e da massa da partícula. Isto é muito útil para os
espectrômetros de massa com campo magnético (ver exercício 6 da
lista 4).
F
v
Figura 9 – Trajetória de uma partícula carregada
(no caso, positiva) num campo magnético uniforme.
Uma importante característica do movimento da partícula é o seu período. Por definição, o período T é o tempo
necessário para a partícula completar uma volta:, portanto, como sua velocidade escalar é v, temos: vT = 2R , ou seja,
v = 2R/T. Substituindo esta expressão para v na primeira equação para R, temos :
T = 2m/qB
ou ainda, lembrando que  =2/T
 = qB/m
que é chamada frequência ciclotrônica.
Com tantas "fórmulas" para decorar, sua lista de impropérios para o velho mestre já deve ter se esgotado. Acalme-se!
Mais vale acender uma vela do que maldizer a escuridão! Na verdade, essas deduções são tão simples que podem irritar
qualquer ser ligeiramente pensante. Tente! Se você está na Unicamp você é mais que ligeiramente pensante!
Força sobre um fio que conduz uma corrente i.
A corrente num fio é o deslocamento de cargas. O sentido convencional da corrente é o de cargas positivas deslocandose. Logo é de se esperar que um fio sofra ação de campo magnético se estiver conduzindo corrente.
L
Vamos considerar que num intervalo de tempo t as
cargas dentro do fio se deslocam de uma distância L
muito pequena. Nesse caso:
v = L/t
i = q/t
ou
q = it
A força sobre a carga q é:
i

F =qBvsenit.B.(L/t).sen, onde B é o
campo magnético no fio e  o ângulo entre B e o fio.
Assim:
B
F
F = iBLsen 
(não precisa decorar!)
Figura 10 – Fio num campo magnético
131
F-107
CAP.VI
Mauro M.G. de Carvalho
Campo devido a uma fio.
O campo magnético em torno de um fio retilíneo, infinito (mas nem tanto!) e conduzindo uma corrente i é dado por:
B
r
i
(ar)
μ i
o , onde  é a permeabilidade magnética do vácuo
o
2ππ
e vale: o = 4 x 10-7 u(SI). (Não precisa decorar!)
A direção do campo é perpendicular ao fio e o sentido é o do
fechamento da mão direita que tem o polegar apontando no
mesmo sentido da corrente (isto precisa saber!), conforme
mostra a figura 12.
Figura 11 – Campo devido a um fio
Figura 12 - Regra da mão direita para campo de um fio
Aplic. 22: Dois fios paralelos e distantes d entre si, conduzem correntes iguais a i 1 e i2. Determine a força por unidade
de comprimento entre eles:
a) no caso das correntes terem o mesmo sentido.
b) no caso das correntes terem sentidos opostos i
132
F-107
CAP.VI
Mauro M.G. de Carvalho
Campos magnéticos importantes.(não precisa decorar as equações!)
B
i
B
i
Campo no centro de uma espira
B= oi/2R
i
Campo no interior de um solenóide. É aproximadamente
uniforme e vale: B = oni, onde n é o número de espiras por
unidade de comprimento.
Fluxo de campo uniforme através de uma superfície plana: É o produto da componente do campo na direção normal
à superfície pela área da superfície.
 =B.A.cos
B
Lei de Faraday
A força eletromotriz induzida num circuito fechado é numericamente igual ao valor absoluto da taxa de variação de
fluxo magnético no circuito.
E
dφ
dt
A corrente induzida é tal que cria um campo oposto à variação do fluxo.
Aplic. 23: Determine a força eletromotriz induzida numa espira quadrada de 2cm de lado quando o campo magnético
uniforme e perpendicular a seu plano varia de acordo com a equação:
a) B(t) = 2t
b) B(t) = 2t – t2
Aplic. 24: No exercício anterior, representar o sentido da corrente.
133
F-107
CAP.VI
Mauro M.G. de Carvalho
Aplic. 25: Considere uma espira quadrado de lado a girando num campo magnético uniforme B com velocidade angular
constante , conforme a figura.
a) Determine o fluxo através da espira.
b) Se a resistência da espira é R, determine a corrente que a percorre. Faça um gráfico da corrente em função do tempo.
eixo de
rotação
Exercícios
1) Qual a massa de um grupo de prótons cuja carga total é 1C? Qual a carga total de 1kg de prótons?
dado: mp = 1,67x10-27 kg
R: 1,04x10-8 kg; 0,96x108 C
2) A massa de um elétron é 9,1x10-31 kg e a do próton 1,67x10-27 kg. A constante de gravitação universal vale 6,67x1011
u(SI). calcule a razão entre as forças de atração gravitacional e elétrica entre um próton e um elétron.
-4 C
3) Calcule a força sobre uma carga de 10-10 C nos pontos A e B da figura ao lado.
R: 0,176 N e 1,8 N
1,0m
0,5m
B
1,0m
4C

2,5m
A
4) O campo elétrico num determinado ponto vale 300V/cm na direção e sentido do eixo X. Qual a força que atuaria
numa carga de –2mC colocada no ponto considerado.
R: 60 N na direção x e sentido –x
5) A Figura abaixo representa um campo elétrico, através de linhas de força, e quatro pontos .
a) Em qual dos pontos o campo elétrico é mais intenso?
b) Em qual dos pontos o campo é horizontal?
c) Em qual dos pontos o campo pode ser considerado uniforme?
B
d) Desenhe o vetor força para uma carga positiva colocada em D;
A
e) Idem para uma carga negativa colocada em B.
C
R: a) C; b) A e C; c) A
134
D
F-107
CAP.VI
Mauro M.G. de Carvalho
6) Considere os pontos A e B do campo elétrico uniforme de 1000V/m representado abaixo.
B'
A
B
0,50 m
a)
b)
c)
d)
e)
f)
g)
h)
Qual a força elétrica que atua numa carga de 20 C em A? E em B?
Qual o trabalho da força elétrica para deslocar a carga de A até B? E de B até A?
Onde a energia potencial da carga é maior, em A ou em B?
Onde o potencial é maior, em A ou em B?
Responda aos itens a e b considerando uma carga de –20C.
Determine a diferença de potencial entre A e B
Determine a diferença de potencial ente B e B’.
Desenhe uma equipotencial que passe por A e outra que passe por B.
R: a) 2,0x10-2N no sentido das linhas de força; b)1,0 x10-2J c) -1,0x10-2J; d) 2,0x10-2N no sentido oposto ao das linhas
de força; Os mesmos com os sinais invertidos; f) 500V; g) zero
7) Considere um sólido qualquer (uma batata, por exemplo) carregado com carga q positiva. Qual o campo para pontos
a uma distância r do sólido, r sendo muito maior que a maior dimensão do sólido.
R: É o mesmo que o de uma carga pontual q no lugar do sólido.
8) Num tubo de raios catódicos, um elétron é acelerado, a partir do repouso, por uma diferença de potencial de 16kV.
Qual a energia cinética final do elétron? Qual sua velocidade?
Dado: me = 9,1 x 10-31 kg
R: 16keV; 7,5x107m/s
9) Resolva o problema anterior para uma partícula . A partícula  é o núcleo de um átomo de He.
Dados: mp ≈ mn = 1,67 x 10-27 kg
R: 1,24x106 m/s
10) Duas placas metálicas de 10x10 cm2 são colocadas face-a-face e ligadas numa fonte de tensão fixa de 500V. Se à
distância entre as placas é 10cm, qual o campo elétrico entre elas? Qual a carga em cada placa?
R: 5000V/m – 4,4x10-4 C
11) Experiência de Millikan -A massa m de uma gotícula de óleo pode ser facilmente calculada conhecendo seu
diâmetro e a densidade do óleo . Suponha que uma gotícula. carregada com N elétrons (o que também não é difícil se
fazer em laboratório) entra, por cima, numa região entre
pulverizador
duas placas paralelas, horizontais e submetidas a uma ddp
...
V que pode ser variada. Um operador (em geral, aluno)
ionizador
observa, através de uma luneta, as gotículas passarem e
.
tenta, até conseguir, parar uma. Conhecendo a massa m da
Olho do aluno
.
gotícula, a distância d entre as placas, a ddp V aplicada e a
d
.
aceleração local da gravidade qual a carga da gotícula?
Como, com muitas repetições desta medida pode-se chegar
Fonte de tensão
ao valor da carga do elétron?
variável
lâmpada
R: q = mdg/V
135
F-107
CAP.VI
Mauro M.G. de Carvalho
12) Nos trechos de circuitos abaixo, calcular :
a) A corrente em cada resistor;
b) A ddp em cada resistor;
c) A ddp entre A e C
d) A potência dissipada em cada resistor
6
3
B
C
8
I=9A
R: a) 3A (6) , 6A(3) e 9A (8); b) 18V (6 e 3e 72V; c) 90V; d) 54W (6), 108W (3) e 648W (8)
F
13) Na figura, cada lado do hexágono é um fio de resistência 1,0 e C é um capacitor de
20 F.
a) Uma tensão de 15 V é aplicada entre A e D. Calcule a corrente em cada fio;
b) Nas mesmas condições, determine a carga no capacitor;
c) Nas mesmas condições, determine a ddp ente B e C;
R: a) 5,0A; b) 3,0x102C; c) 5,0 V
E
C
D
A
B
14) No circuito , r1 e r2 são as resistências internas do voltímetro e do
amperímetro respectivamente. Calcular a corrente e a tensão em R (R= 8)
considerando:
a) S1 aberta e S2 na posição 1;
R: 1 A
b) S1 fechada e S2 na posição1;
R: 10(8+r1)/(10r1+16)
c) S1 aberta e S2 na posição 2;
R: 10/(10+r2)
d) Em que condições r1 teria pouca influência no circuito?
R: r1>>8
e) Em que condições r 2 teria pouca influência no circuito?
R: r2<<8
C
V
E = 10V
r=2
r1
R
1
S1
S2
A
r2
2
15) Uma partícula  (2 prótons + 2 nêutrons) com energia de 1,0MeV penetra num campo magnético uniforme de
2000G. A velocidade da partícula é perpendicular ao campo.
(a) Determine o raio do círculo descrito pela partícula;
R: 0,72m
(b) Determine o tempo para a partícula descrever meia volta.
R: 6,5x10-7s
16) Um feixe de elétrons de 10keV penetra numa região de campo magnético uniforme perpendicular a esta folha. A
trajetória do feixe é mostrada abaixo. Determine:
(a) O(s) sentido(s) do(s) campo(s);
R: Entrando na folha no 1o arco e saindo no segundo
(b) O(s) módulo(s) do(s) campo(s);
R: 200G
3,4cm
3,4cm
17) Um anel no plano desta folha e 1,0cm2 de área tem uma resistência de 10. Um campo magnético, uniforme e
perpendicular à folha, é ligado e cresce, saindo da folha, até o valor de 4000G segundo a equação B(t) = 1000t (B em
Gauss e t em segundos).
(a) Indique o sentido da corrente no anel;
R: Horário
(b) Determine a corrente em função do tempo.
R: 1A
136
F-107
CAP.VI
Mauro M.G. de Carvalho
18) No problema anterior, o campo é desligado e diminui linearmente segundo a equação B(t) =
4000 – 100t (B em Gauss e t em segundos).
(a) Indique o sentido da corrente no anel;
(b) Determine a corrente em função do tempo enquanto o campo diminui.
(constante)
R: Anti-horário
R : i = 100mA
19) Na figura abaixo, calcule a força (módulo, direção e sentido) na espira de 40x60 cm2 percorrida por uma corrente
de 100mA. O módulo de B é 0,5T.
R: 2x10 –2 N
40 cm
60 cm
20) Acelerado por uma ddp V, um feixe de ions positivos de massa m penetra num campo magnético uniforme B
conforme mostra a figura abaixo. Os ions têm carga +e (ionização simples). (a) Determine D.
(b) Determine D para
ions de ionização dupla. Considere íons de H , C e N, todos com carga +e. Para um campo magnético de 0,5T, e ddp
V = 10kV, calcule D para os três casos.
2 V 12
2 2V 12
m
m
R: (a) D 
(b) D 
B e
B e
Canhão de íons
D
(c)DH= 5,0 cm; DC = 17,4 cm; DN = 18,7 cm
137