Electricidade e Magnetismo

CAMPOS ELÉCTRICOS
Formalismo do
Electromagnetismo
(equações de Maxwell)
Explicativo de todos os fenómenos que
envolvem propriedades eléctricas e
magnéticas
PROPRIEDADES DAS CARGAS ELÉCTRICAS
• Existem dois tipos de cargas: positivas e negativas.
• As cargas conservam-se.
• Existem forças de atracção e de repulsão entre as cargas, caso sejam de sinais
contrários ou do mesmo sinal, respectivamente.
• Estas forças são proporcionais ao inverso do quadrado da distância entre as cargas.
ISOLADORES E CONDUTORES
• Quanto à capacidade de transportar cargas eléctricas, os materiais dividem-se em:
(i)
Condutores – possuem cargas eléctricas livres.
(ii)
Isolantes – têm dificuldade em transportar carga eléctrica.
(iii)
Semi-condutores – possuem propriedades intermédias.
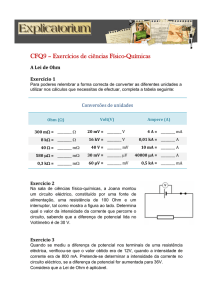
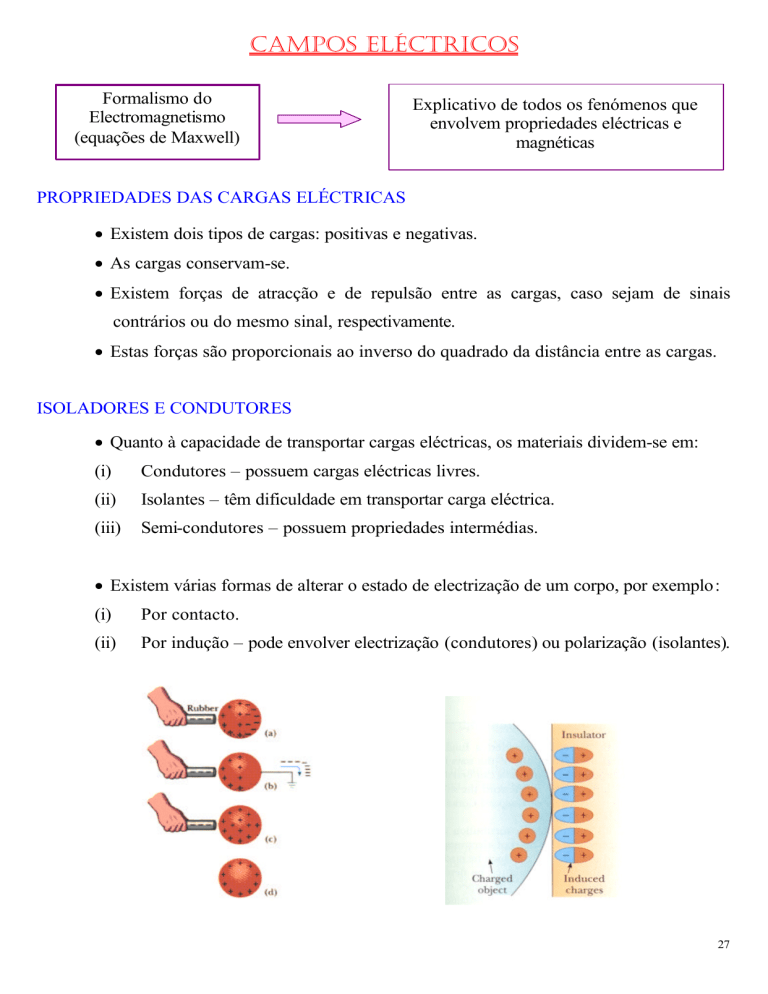
• Existem várias formas de alterar o estado de electrização de um corpo, por exemplo:
(i)
Por contacto.
(ii)
Por indução – pode envolver electrização (condutores) ou polarização (isolantes).
27
LEI DE COULOMB
•
A lei de Coulomb foi uma lei estabelecida com base nos
seguintes dados experimentais:
(i) A força eléctrica entre duas cargas tem a direcção da
linha que as une,
(ii) é inversamente proporcional ao quadrado da distância
entre elas,
(iii) é proporcional ao produto das cargas,
(iv) é atractiva quando as cargas têm sinais contrários e
repulsiva, quando têm sinais iguais.
•
Matematicamente, a lei é expressa através da relação:
r
1
qq r
= 8.9875×109 Nm 2 / C 2 ,
Feléc = k e 1 2 2 u r , com ke a constante de Coulomb: k e =
4πε 0
r
e ε 0 a permitividade do vazio: ε 0 = 8.8542×10 C / Nm
-12
2
2
• Como seria previsível pelo cálculo
vectorial, também as forças eléctricas
cumprem o princípio da sobreposição
das forças. De modo que a força que
actua sobre uma partícula é a soma de
todas as forças exercidas sobre ela.
• Como exemplo ilustrativo, considerar duas cargas positivas q1 e q2 e uma terceira
carga negativa, q3, num ponto da linha que une as duas primeiras. Pode
demonstrar-se que a coordenada em que a força aplicada à partícula q3 dada por:
x=
(
L q1 ± q1 q 2
(q1 − q2 )
)
CAMPO ELÉCTRICO
• O campo eléctrico é definido pela razão entre a força eléctrica que actua sobre uma
carga de prova positiva colocada num determinado ponto do espaço e o valor dessa
carga.
28
r
r
F
Qr
Eeléc =
= ke 2 u r
q0
r
•
Tendo em conta esta definição, facilmente se conclui que:
(i)
O campo tem sempre a direcção e sentido da força.
(ii) O campo é independente da partícula de prova, dependendo
apenas das cargas que lhe dão origem.
(iii) O campo existe mesmo na ausência da carga de prova.
(iv) A carga de prova deve ser tão
pequena quanto possível, para que
não interfira no campo que está estabelecido.
•
Como exemplo ilustrativo, pode considerar-se o campo eléctrico
criado por um dipolo:
Eeléc = k e
2qa
y3
CAMPO ELÉCTRICO DE UMA DISTRIBUIÇÃO CONTÍNUA
• Considera-se uma distribuição contínua quando a distância entre as cargas é muito
menor do que a distância ao ponto de medida.
• Para o cálculo do campo eléctrico produzido por uma
distribuição contínua de cargas, utiliza-se o estratagema de
dividir o volume total em volumes infinitesimais correspondentes
a cargas ∆q.
• Nesse caso o campo será dado por:
r
∆q r
∆q r
dq r
Eeléc = k e ∑ 2 i uri = k e lim ∑ 2 i uri = k e ∫ 2 ur
∆qi →0
ri
ri
r
i
i
• Na abordagem contínua, surgem conceitos importantes como as
densidades de carga volúmica, superficial e linear:
ρ≡
Q
V
s ≡
Q
A
λ≡
Q
, válidas para distribuições uniformes de carga, de um
l
modo mais geral, temos:
29
ρ≡
dQ
dV
s≡
dQ
dA
λ≡
dQ
dl
• Como exemplo ilustrativo, pode considerar-se o campo eléctrico criado por uma
barra carregada:
E = ke
Q
d (l + d )
LINHAS DE CAMPO ELÉCTRICO
• As linhas de campo eléctrico relacionam-se com este da seguinte forma:
(i)
O vector campo eléctrico é tangente às linhas de
campo.
(ii)
O nº de linhas de campo por unidade de área que
atravessam uma superfície perpendicular ao
campo é proporcional à amplitude do campo
nessa região.
• Propriedades das linhas de campo:
(i)
As linhas começam nas cargas positivas e terminam nas negativas (ou então
começam ou acabam no infinito se a carga total não for nula).
(ii)
O nº de linhas que chegam ou partem de uma carga é proporcional à sua
amplitude.
(iii)
As linhas não se cruzam.
• Verifique-se que esta forma de desenhar linhas de campo é compatível com a lei de
Coulomb. É fácil provar que:
Eα
N
, desde que se considere uma esfera centrada numa carga pontual
4πr 2
• Debilidades desta representação:
(i)
Dão a ilusão de que o campo eléctrico é descontínuo.
30
(ii)
Aparecem
como
uma
representação
bi-dimensional de uma realidade
tri-dimensional.
• Exemplos de distribuição de linhas de campo devido a várias conformações de carga:
a)
b)
c)
d)
e)
• Repare-se que num ponto afastado as linhas c), d) e e) são semelhantes às a) e b).
MOVIMENTO DE PARTÍCULAS CARREGADAS NUM CAMPO UNIFORME
• Repare-se que uma carga que seja colocada num campo eléctrico uniforme, fica
sujeita a uma força, pelo que terá um movimento uniformemente acelerado, com
aceleração:
r
r qE
a=
m
• Se a partícula for positiva a aceleração terá o sentido do campo, caso contrário terá o
sentido contrário.
• É com base neste resultado que se constroem os osciloscópios:
31
LEI DE GAUSS
Forma alternativa de calcular o campo eléctrico
criado por uma distribuição de cargas
Lei de Gauss
FLUXO ELÉCTRICO
• O fluxo eléctrico numa determinada superfície é definido como o nº de linhas de
campo que a atravessam.
• Então, o fluxo eléctrico através de uma superfície fechada vai ser proporcional à
carga no seu interior e não irá depender da forma dessa
superfície.
• Comece-se por calcular o fluxo eléctrico numa situação
simples – considere-se um campo eléctrico uniforme E
e uma superfície A que lhe é perpendicular. O fluxo
vem dado por:
N
φ = E.A porque: φ = N = A = EA (N m2 / C)
A
• Se a superfície não for perpendicular ao campo,
temos:
r r
φ = E.A cosϑ , sendo ϑ o ângulo entre E e A .
• No caso mais geral em que o campo eléctrico varia em redor da superfície tem-se:
r r
φ = lim ∑ Ei .∆Ai =
∆Ai →0
i
r r
∫ E.dA
sup
• E no caso de uma superfície fechada, obtém-se:
r r
φ = ∫ E.dA = ∫ En dA ,
sendo En a componente do campo normal à superfície.
32
LEI DE GAUSS
•
A Lei de Gauss fornece uma relação entre o fluxo calculado
através de uma superfície fechada e a carga existente no seu
interior.
•
O cálculo do fluxo através de uma esfera que envolve uma
carga Q positiva vem dado por:
φ=
•
Q
ε
Na verdade, mesmo que a superfície considerada não seja esférica, o fluxo será igual, uma
vez que é proporcional ao número de linhas de campo.
•
Quanto ao fluxo de um campo criado por cargas no exterior da
superfície considerada, facilmente se verifica que é nulo.
•
Combinando os dois resultados e admitindo, uma vez mais, a
sobreposição dos campos:
r r Qint
φ = ∫ E.dA =
ε
“O fluxo através de qualquer superfície fechada é igual à carga no seu interior dividida pela
constante ε”
•
Nos problemas em que a Lei de Gauss é utilizada, deve ter-se em atenção o seguinte:
(v) A superfície considerada não tem, necessariamente, realidade física.
(vi) Esta é uma abordagem muito útil para casos em que seja evidente um elevado nível de
simetria.
(vii) A escolha da superfície é crucial.
APLICAÇÕES DA LEI DE GAUSS A ISOLANTES CARREGADOS
•
Calcule-se o campo criado por uma esfera isolante com densidade de carga ρ e carga total
positiva Q. (considere-se pontos no interior e no exterior da esfera).
Q
E
=
k
e 2
no exterior:
r
33
Q
E
=
k
r
e
no interior:
3
a
•
Calcule-se o campo criado por um fio infinito com densidade de carga linear, λ, constante:
E = ke
•
2λ
r
Calcule-se o campo criado por um plano infinito com densidade de carga superficial, σ,
constante:
E=
σ
2ε
CONDUTORES EM EQUILÍBRIO ELECTROSTÁTICO
•
Um condutor diz-se em equilíbrio electrostático quando não existe movimento de cargas
no seu interior. Nestas condições mostra-se que:
(i)
O campo eléctrico no seu interior é nulo.
Caso contrário as cargas tenderiam a se mover.
(ii) As cargas existentes no interior do condutor encontram-se à superfície.
r
Se: Eint = 0
⇒
Q = 0 e, portanto, as cargas só poderão estar à superfície
do condutor.
(iii) O campo eléctrico fora do condutor, mas junto à fronteira, é perpendicular à superfície e
tem amplitude: σ / ε 0.
Se fosse tangencial as cargas encontrar-se-iam em movimento.
Pela Lei de Gauss, prova-se a sua amplitude.
34
POTENCIAL ELÉCTRICO
O potencial
eléctrico
Permite uma abordagem energética dos
problemas de electromagnetismo.
DIFERENÇA DE POTENCIAL E POTENCIAL ELÉCTRICO
• Comece-se por calcular o trabalho realizado por uma força eléctrica sobre uma carga
sujeita a um campo eléctrico:
B
r r
r r
WFe = ∫ Fe .ds = q 0 ∫ E.ds
B
A
A
• Se a este trabalho for associada uma variação de energia potencial ∆U , tem-se:
B r
r r
r
WFe = − ∆U ⇔ ∆U = −q0 ∫ E.ds ⇔ U f − U i = − q0 ∫ E.ds ⇔
B
A
⇔
U f −Ui
q0
A
B r
r r
r
= − ∫ E.ds ⇔ ∆V = − ∫ E.ds
B
A
A
• Onde a quantidade U/q0 é definida como a função potencial eléctrico.
• Repare-se que o potencial eléctrico é dependente do campo, mas independente da
carga, enquanto a energia eléctrica depende de ambos.
• O potencial eléctrico exige a definição de uma referência. Por convenção, o potencial
num ponto infinito é nulo. Então: “ O potencial eléctrico num qualquer ponto P é o
trabalho por unidade de carga realizado sobre uma partícula positiva para a fazer
mover do infinito até esse ponto.”
• A unidade de potencial eléctrico é o volt (V), que equivale a 1J/1C.
DIFERENÇAS DE POTENCIAL NUM CAMPO ELÉCTRICO UNIFORME
•
A diferença de potencial criada por um campo uniforme vem dada por:
∆V = − Ed
o que pode ser verificado pensando no que se passa com uma partícula que é trazida de um
ponto A para um ponto B, onde está estabelecido um campo eléctrico com a mesma linha de
acção.
35
•
Enquanto que a variação de energia potencial, vem dada por:
∆U = −q0 Ed
•
•
Se o deslocamento não acontecer segundo a direcção do campo:
rr
∆V = − E.s = −Ed
Donde resulta que qualquer plano perpendicular a um campo eléctrico uniforme se
encontra ao mesmo potencial.
•
Define-se superfície equipotencial como o lugar geométrico que se encontra ao mesmo
potencial eléctrico.
POTENCIAL ELÉCTRICO E ENERGIA POTENCIAL DEVIDOS A UMA DISTRIBUIÇÃO
DE CARGAS
•
A diferença de potencial criado por uma carga pontual vem
dada por:
1 1
∆V = k e q − 
 rB rA 
36
•
Pensando que no infinito (r = ∞), V = 0, então:
V = ke
•
q
r
Donde resulta:
V = ke ∑
i
q1q2
qi
U
=
k
e
r1,2 para a
ri , para um conjunto de partículas carregadas, e
energia potencial referente à interacção de duas partículas carregadas.
•
E no caso de uma distribuição de cargas contínua:
V = ke ∫
dq
r
CÁLCULO DO CAMPO ELÉCTRICO A PARTIR DO POTENCIAL
•
r
r r
r
r
dV r
u
Conforme já vimos: dV = − E.ds . Se E tiver a direcção x, vem: E = E x u x = −
dx x
•
Ou, numa situação mais geral:
r
r
∂V
∂V
∂V
Ex = −
, Ey = −
, Ez = −
⇒ E = −∇V = −grad V
∂x
∂y
∂z
•
Ou seja, as superfícies equipotenciais são sempre perpendiculares ao campo, tendo este a
direcção dos potenciais mais baixos.
37
POTENCIAL DE UM CONDUTOR CARREGADO
•
Repare-se que num condutor carregado se verifica:
i)
dois pontos na superfície têm o mesmo potencial.
ii)
qualquer ponto no seu interior têm o mesmo potencial.
iii)
o campo eléctrico numa cavidade no seu interior é nulo (possibilidade de
blindar um circuito…)
APLICAÇÕES
ke Q
•
Anel: V =
•
k e Q  l + l 2 + d 2
Barra: V = l ln
d

x2 + a 2




38
CAMPOS MAGNÉTICOS
Existência de
pólos magnéticos
Descoberta do magnetismo
Relação entre a electricidade e o magnetismo
– surgimento do electromagnetismo
O CAMPO MAGNÉTICO
• Os campos magnéticos são gerados na presença de ímanes ou de cargas eléctricas em
movimento.
• Analogamente ao campo eléctrico, a existência de um campo magnético é
comprovada através da presença de um objecto de prova. Neste caso é uma partícula
carregada animada de velocidade.
• Nestas condições, verificou-se que:
iv)
A amplitude da força magnética a que a partícula fica sujeita é proporcional
à sua carga e à sua velocidade.
v)
A amplitude da força magnética é proporcional à amplitude do campo
magnético.
vi)
Se a velocidade da partícula for paralela à direcção do campo, a força será
nula.
vii)
A força é perpendicular ao plano formado pela velocidade da partícula e
pelo campo magnético.
viii) O sentido da força sobre uma carga positiva é o oposto ao que fica sujeita
uma carga negativa.
ix)
A amplitude da força é proporcional ao seno do ângulo formado pela
velocidade e pelo campo magnético.
• Estas observações conduzem à expressão:
r
r
r r
Fmag = qv × B , sendo Fmag a força magnética a que fica sujeita uma partícula
r
r
v
de carga q, animada de uma velocidade , sob a acção de um campo magnético B .
39
• Repare-se que:
i)
Enquanto a força eléctrica é paralela ao campo eléctrico a força magnética é
perpendicular ao campo magnético.
ii)
A força eléctrica actua sobre cargas em repouso a força magnética actua sobre
cargas em movimento.
iii)
A força eléctrica realiza trabalho ao deslocar uma partícula, a força magnética
não (desde que o campo seja estacionário).
• A unidade de campo magnético no SI é o Tesla (T).
FORÇA MAGNÉTICA NUM CONDUTOR ATRAVESSADO POR UMA CORRENTE
•
Seja uma corrente eléctrica definida pela relação:
I=
•
dq
dt
Pode pensar-se o que acontece quando uma corrente eléctrica fica sujeita a um campo
magnético - repare-se que uma corrente eléctrica é um fluxo de cargas em movimento.
•
Considere-se, então, um fio de área A, comprimento l, mergulhado num campo magnético
r
B , uniforme e no interior do qual se movem n cargas q por unidade de volume, com
velocidade v. A força exercida sobre o fio será:
(
)
r
r r
Fmag = qv × B nAl
40
•
Mas, pensando que a corrente eléctrica vem dada por:
I=
•
∆Q nqA∆x
=
= nqAv , então:
∆t
∆t
r
r r
Fmag = I L × B
Para um fio de forma arbitrária, teremos a generalização:
r
r
r r
r r
dFmag = I ds × B ou: Fmag = ∫ I ds × B
CASO I: Campo magnético uniforme e corrente eléctrica constante:
r
r
r r
b r


Fmag = I  ∫ ds  × B = IL × B , porque
 a 
r
d
s
∫a é a soma vectorial de todos os vectores
b
infinitesimais que compõem o percurso.
CASO II: Percurso fechado num campo magnético uniforme e percorrido por uma corrente
constante:
r
r r
b r


Fmag = I  ∫ ds  × B = 0 , porque
 a 
∫
b
a
r r
ds = 0
MOVIMENTO DE UMA PARTÍCULA CARREGADA NUM CAMPO MAGNÉTICO
•
Aplique-se a lei de Newton a uma partícula carregada, animada de uma velocidade, sob a
acção de um campo magnético perpendicular à sua velocidade.
•
Nestas condições a força é central, pelo que a trajectória da partícula será circular e de
raio:
Fmag = qvB = ma ⇔ ... ⇔ r =
•
mv
qB
Se a velocidade da carga tiver uma componente paralela ao campo, então a sua trajectória
será em hélice.
41
LEI DE BIOT-SAVART
r
• Experimentalmente observou-se que o campo magnético dB criado num ponto P
r
devido à passagem de uma corrente I no elemento ds de um fio condutor, cumpre:
r
r
r
r
d
B
x)
é perpendicular a ds e a r , sendo r o vector posição do ponto P.
r
dB é inversamente proporcional a r 2 .
xi)
r
d
B
xii)
é proporcional à corrente I e ao elemento de comprimento ds ..
xiii)
r
dB é proporcional ao sen θ, sendo θ o ângulo formado por dsr e rr .
• Matematicamente pode-se expressar estes resultados, através da expressão:
r r
r
I ds × u r
µ0
dB = k m
k
=
= 10− 7 Tm/A , uma vez que:
m
, sendo
2
r
4π
µ0 - permeabilidade do vácuo tem o valor: 4π ×10 -7 Tm/A .
Que é conhecida como a Lei de Biot-Savart.
• A generalização desta lei para calcular o campo magnético criado por uma
distribuição de correntes, será:
r r
r
I ds × ur
B = km ∫
que é uma expressão com algumas semelhanças
r2
r
dq r
E
=
k
com a encontrada para o campo eléctrico:
∫ r2 u
• Uma aplicação importante desta expressão é o cálculo do campo criado por um
condutor linear rectilíneo:
r µI
B = 0 (cos ϑ1 − cosϑ2 )
4πR
• Ou, se o condutor for considerado infinito:
r µI
B= 0
2πR
42
FORÇA MAGNÉTICA ENTRE DOIS CONDUTORES PARALELOS
•
Calcule-se a força existente entre dois condutores paralelos entre si e que são percorridos
por correntes I1 e I2:
r r
r
r
F1 = I1l × B2 , onde F1 é a força exercida pelo condutor 2
sobre o elemento de comprimento l do condutor 1.
r
Ou seja, B2 é o campo magnético criado pelo condutor 2 no elemento l do condutor 1.
•
Então:
F1 = I1lB2 = I1l
µ0 I 2
II
= µ0 1 2 l , ou, quando
2πa
2πa
se calcula a força por unidade de comprimento:
F1
II
F
= µ0 1 2 = 2
l
2πa
l
•
Quanto ao sentido das forças, facilmente se
verifica que elas serão de atracção quando as
correntes circulam em sentido contrário e de
repulsão, caso contrário.
LEI DE AMPÈRE
•
Tendo em conta o cálculo do campo criado por um fio rectilíneo infinito, determine-se a
•
Na verdade, esta expressão é mais geral, cumprindo-se para qualquer trajectória fechada e
r r
B
quantidade ∫ .ds , nestas circunstâncias:
r r
B
∫ .ds = µ0 I
geometria de correntes estacionárias que se considerem. É conhecida pela Lei de Ampère
e é a lei do magnetismo equivalente à Lei de Gauss.
r r
• Pode enunciar-se da seguinte forma: “O integral da quantidade B.ds através de uma linha
fechada iguala o produto µ0 I , onde I é a corrente estacionária total que atravessa
qualquer superfície delimitada pela linha fechada considerada”.
43
•
Uma aplicação interessante da Lei de Ampère é o cálculo do campo magnético criado por
um solenóide:
i)
Num ponto exterior pode considerar-se o campo magnético nulo.
ii)
Num ponto interior, aplicando a Lei de Ampère à linha fechada apresentada na
figura:
B = µ0 I
N
l
LEI DE FARADAY E LEI DE LENZ
•
A Lei de Faraday indica-nos de que
forma é que campos magnéticos
permitem gerar correntes eléctricas.
•
Se um condutor, no interior do qual
não circulam cargas se deslocar
relativamente a um campo magnético,
as suas cargas vão sofrer uma força
que as impelirá a mover-se.
•
A este fenómeno dá-se o nome de Indução Magnética.
44
•
Similarmente ao que foi feito para o campo eléctrico é possível definir fluxo de campo
magnético através de uma superfície A, através da expressão:
Φ mag
•
r r
= ∫ B.dA
A unidade de fluxo magnético no SI é o Weber (Wb), pelo que é também possível
considerar a unidade de campo como Wb/m2.
•
A forma matemática de formalizar a indução magnética é através da lei de Faraday:
fem = −
dΦ mag
dt
que pode ser enunciada da seguinte forma: “A força electromotriz (diferença de potencial)
gerada por indução iguala, em valor absoluto, a taxa de variação do fluxo de campo magnético
através da superfície delimitada pelo circuito”.
•
O sinal ‘-‘ na expressão indica que “a fem se opõe à causa que lhe deu origem”. Que é a
conhecida Lei de Lenz.
45