Lista1: Cinemática Unidimensional

Lista 8: Dinâmica II: Movimento no Plano
Lista 8: Dinâmica II: Movimento no Plano
NOME:______________________________________________________________________
Matrícula:
Turma:
Prof. :
Importante:
i. As cinco páginas seguintes contém problemas para serem resolvidos e entregues.
ii. Leia os enunciados com atenção.
iii.Responder a questão de forma organizada, mostrando o seu raciocínio de forma coerente.
iv. Analisar a resposta respondendo: ela faz sentido? Isso lhe ajudará a encontrar erros!
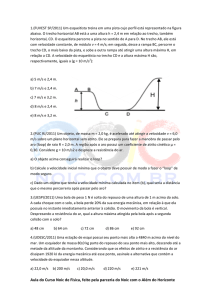
1. Três carros trafegam a 25 m/s na rodovia
mostrada na figura ao lado. O carro B
encontra-se no fundo de um vale, entre as
colinas, e os carros A e C, no topo das
colinas. Tanto o vale quanto a colina em
que se encontra o carro A possuem um raio de curvatura igual a 200m. O topo da colina onde se
encontra o carro C é plano. Suponha que, subitamente, cada carro seja freado fortemente e comece a
derrapar. Quanto vale a aceleração tangencial de cada carro ? Considere μc = 1,0.
1
Lista 8: Dinâmica II: Movimento no Plano
2. Um bloco de 4,00 kg está preso a um poste vertical por dois fios
leves. Quando o sistema gira em torno do poste vertical, os fios
ficam estirados e a tensão no fio de cima é de 80,0 N. (a) Qual é a
tensão no fio na parte inferior? (b) Quantas revoluções por minuto
o sistema realiza? (c) Encontre o número de revoluções por minuto
quando a tensão no fio na parte inferior for igual a zero.
2
Lista 8: Dinâmica II: Movimento no Plano
3. Uma conta pequena pode deslizar sem atrito sobre um aro circular que
está na vertical e tem um raio de r = 0,100 m. O aro gira a uma taxa
constante de 4,00 rev/s em torno de um diâmetro vertical (veja a figura
ao lado). (a) Encontre o ângulo θ no qual a conta está em equilíbrio na
vertical. (b) É possível a conta alcançar a mesma altura que o centro do
aro? O que acontecerá com a conta se o aro girar a 1 rev/s?
3
Lista 8: Dinâmica II: Movimento no Plano
4.
Uma pequena bola de massa m está
sobre o tampo de uma mesa sem atrito.
Um fio leve está amarrado à bola e um
bloco de massa M está pendurado na
outra extremidade do fio. Veja a figura
ao lado. A pequena bola é colocada em
movimento circular de raio r e
velocidade v. Qual deve ser o valor de
v para que o bloco de massa M
permaneça parado quando liberado?
4
Lista 8: Dinâmica II: Movimento no Plano
5.
Uma partícula move-se numa superfície horizontal sem
atrito ao longo de um caminho mostrado, visto de
cima, na figura ao lado. A partícula está inicialmente
em repouso em A e então começa a se mover em
direção ao ponto B, ganhando velocidade a uma taxa
constante. De B para C a partícula move-se ao longo
de um caminho circular com velocidade constante. A
velocidade permanece constante ao longo da linha reta
que liga C a D. De D a E a partícula move-se ao longo
de um caminho circular, mas agora sua velocidade está
decrescendo a uma taxa constante. A velocidade
continua a decrescer com uma taxa constante quando a
partícula desloca-se de E para F. A partícula para em F. Em cada ponto marcado com uma
bolinha preta, desenhe setas representando a velocidade, a aceleração e a força resultante
atuando sobre a partícula. Desenhe setas mais curtas ou mais longas para representar vetores de
maior ou menor módulo. (Os intervalos de tempo entre os pontos marcados não são iguais).
5
Lista 8: Dinâmica II: Movimento no Plano
Questões Conceituais:
(A) Em um mundo sem atrito, quais das seguintes atividades você poderia (ou não poderia) fazer? Explique
seu raciocínio. (a) Dirigir numa estrada curva na qual as curvas não possuem inclinação. (b) Pular no
ar. (c) Começar a andar numa calçada horizontal. (d) Subir uma escada vertical. (e) Mudar de faixa
numa autoestrada.
(B) Um avião a jato voa com velocidade constante mantendo um curso nivelado com o solo. Os motores
funcionam a pleno vapor.
a. Qual é a força resultante sobre o avião? Explique.
b. Desenhe um diagrama de corpo livre do avião visto de lado com o avião voando para a direita.
Denomine (não apenas indique) todas as forças mostradas no seu diagrama.
c. Aviões se inclinam lateralmente quando eles fazem a curva. Desenhe um diagrama de corpo livre do
avião visto por trás, quando ele faz a curva para a direita.
d. Por que aviões se inclinam lateralmente quando eles fazem uma curva? Explique.
(C) A figura ao lado mostra duas bolas de mesma massa movendo-se em
círculos verticais. A tensão na corda A é maior, menor ou igual à tensão na
corda B se as bolas passam pelo topo dos círculos (a) com velocidades
iguais (b) com velocidades angulares iguais?
(D) Um pequeno projétil é lançado paralelo ao solo de uma altura h = 1 m com
velocidade suficiente para orbitar um planeta completamente liso e sem
atmosfera. Um inseto está dentro de um pequeno buraco no projétil. O inseto encontra-se em
imponderabilidade? Explique.
(E) Satélites são mantidos em órbita pela força gravitacional atrativa que a Terra exerce sobre eles. Um
satélite numa órbita de raio r em torno da Terra move-se com uma velocidade maior que a velocidade
de um satélite numa órbita de raio maior que r.. Baseado nesta informação, o que você pode concluir
sobre a força atrativa da Terra sobre o satélite? (i) Ela cresce quando a distância do satélite à Terra
cresce. (ii) A força tem a mesma intensidade para todas as distâncias do satélite à Terra. (iii) Ela
decresce quando a distância do satélite à Terra cresce. (iv) A informação dada não é suficiente para
responder a questão.
6
Lista 8: Dinâmica II: Movimento no Plano
Exercícios e Problemas:
1. Um motociclista audacioso planeja decolar de uma rampa com 2,0 m de altura, inclinada em 200 ,
projetar-se por sobre uma piscina de 10 m cheia de crocodilos famintos e aterrissar no solo plano do
outro lado. Ele treinou isso várias vezes e estava bastante confiante. Infelizmente, o motor da moto
para de funcionar no momento em que ele começa a subir a rampa. Neste instante ele está a 11 m/s e
o atrito de rolamento dos seus pneus de borracha não é desprezível. Ele sobreviverá ou se tornará
comida de crocodilo?
2. Um disco de hóquei no gelo é impulsionado por um foguete que gera um empuxo de 2,0 N. A massa
total do conjunto é de 1.0 kg e ele é liberado a partir do repouso sobre uma mesa livre de atrito, com
uma altura igual a 2,0 m, de um ponto situado a 4,0 m da borda. O nariz do foguete aponta
perpendicularmente à borda. A que distância horizontal da borda da mesa o disco aterrissará?
3. Uma bola de 100 g, presa a um barbante de 60 cm de comprimento, gira em um círculo vertical em
torno de um ponto a 200 cm do piso. Subitamente, o barbante se rompe quando está paralelo ao
solo, com a bola se movendo para cima. A bola atinge uma altura de 600 cm acima do piso. Quanto
vale a tensão imediatamente antes do barbante se romper?
4. Considere uma estrada que possui uma curva
inclinada de ângulo θ = 250 e raio de curvatura r =
50 m. A estrada está molhada. O coeficiente de
atrito estático entre os pneus e a estrada é μe = 0,30
e o coeficiente de atrito cinético μc = 0,25. (a) Qual
é a maior velocidade que um automóvel pode ter
antes que deslize inclinação acima? (b) Qual é a
menor velocidade que o automóvel pode ter antes
de deslizar inclinação abaixo?
5. Propõe-se que, no futuro, as estações espaciais
gerem gravidade artificial por meio de rotação. Suponha que uma estação seja construída na forma
de um gigantesco cilindro com 1.000 m de diâmetro que gira em torno de seu eixo. A superfície
interior constitui o convés da estação espacial. Que período de rotação estabelecerá a gravidade
"normal"?
Exercício corrigido em aula de monitoria.
6. Num parque de diversões, passageiros ficam de pé junto às
paredes de um anel giratório de 16 m de diâmetro. Depois que o
anel adquiriu velocidade suficiente, ele passa para uma posição
vertical, como mostrado na figura ao lado.
(a) Suponha que o anel complete cada volta em 4,5 s. Se a massa
de uma passageira é 55 kg, com que intensidade de força o anel
a empurrará no topo de uma volta? E no fundo?
(b) Qual é o máximo período de rotação do anel que impedirá os
passageiros de caírem quando passarem pelo topo?
7
Lista 8: Dinâmica II: Movimento no Plano
7. Satélites de comunicação são colocados em órbitas circulares onde eles permanecem diretamente
acima de um ponto fixo no equador enquanto a Terra gira. Estas órbitas são chamadas órbitas
geossíncronas. A altitude de uma órbita geossíncrona é de 3,58 x 107 m.
(a) Qual é o período de um satélite numa órbita geossíncrona?
(b) Encontre o valor de g nesta altitude.
(c) Qual é o peso de um satélite de 2 000 kg numa órbita geossíncrona?
8. Um pêndulo cônico é formado prendendo-se uma bola de 500 g à
extremidade de um fio de 1,00 m de comprimento. A outra
extremidade é presa ao teto e a massa é colocada movendo-se num
círculo horizontal de raio igual a 20,0 cm. A figura ao lado mostra que
o fio descreve a superfície de um cone. Daí o nome.
(a) Qual é a tensão no fio?
(b) Qual é a velocidade angular da bola em rpm?
9. Você está voando para Nova York e acaba de ler uma revista de bordo que traz um artigo sobre a
física do voo. Você aprendeu que o fluxo de ar sobre as asas cria uma força de sustentação que é
sempre perpendicular às asas. Em voo nivelado, a sustentação orientada para cima, contrabalança
exatamente a força gravitacional dirigida para baixo. O piloto diz pelos fones que, devido ao tráfego
aéreo intenso, o avião vai permanecer circulando ao redor do aeroporto por algum tempo. Ele diz
que manterá o avião a uma velocidade de 400 mph e a uma altitude de 20.000 pés. Então, você
começa a se indagar sobre o diâmetro do círculo horizontal descrito pelo avião ao redor do
aeroporto. Você percebe que o piloto inclinou lateralmente o avião, de modo que as asas formem 100
com a horizontal. O cartão de instruções sobre segurança, na bolsa da parte de trás do banco da
frente, informa que o comprimento da asa do avião é de 250 pés. O que você pode descobrir a
respeito do diâmetro?
Exercício corrigido em aula de monitoria.
10. Um pequeno bloco de massa m é colocado dentro de um cone invertido
que está girando em torno de um eixo vertical de modo que o tempo de uma
volta do cone é T. As paredes do cone fazem um ângulo β com a vertical. O
coeficiente de atrito estático entre o bloco e o cone é μ. Se o bloco deve
permanecer a uma altura h acima do vértice do cone, quais são os valores
máximo e mínimo de T?
8
Lista 8: Dinâmica II: Movimento no Plano
RESPOSTAS:
1) Comida de crocodilo.
2) 3,0 m
3) 13,1 N
4) (a) 21 m/s; (b) 8,5 m/s
5) 45,0 s
6) (a) 3,2 x 102 N, 1,4 kN; (b) 5,7 s
7) (a) 24,0 h; (b) 0,223 m/s2; (c) 0 N
8) (a) 5,00 N; (b) 30 rpm
9) 37 km
Tmin  2
h tan   sen   cos  


g  cos   sen 
Tmax  2
h tan 
g
10)
 sen   cos  


 cos   sen 
9