lentes esfericos (teo-exp)

30/05/2014
1
DEFIJI
Semestre 2014 - 1
Ótica – Lentes
Esféricos
Prof. Robinson
10:07:19
1
INTRODUÇÃO
O ÍNDICE DE REFRAÇÃO
Quando a luz passa de um meio para outro, sua velocidade
aumenta ou diminui devido as diferenças das estruturas atômicas
das duas substâncias, ou de suas densidades ópticas ou índices de
refração.
O índice de refração absoluto de um meio pode ser obtido
experimentalmente e é dado pela relação:
=
Onde, c = velocidade da luz na vácuo e
v= velocidade da luz para um comprimento de onda específico
num certo meio.
1
30/05/2014
INTRODUÇÃO
ÍNDICES DE REFRAÇÃO DE ALGUMAS SUBSTÂNCIAS
O índice de refração da luz no vácuo é considerado
arbitrariamente como sendo igual a 1, que é praticamente aquele
obtido para o ar: 1,00029 (temperatura de 15oC e 1 atm de
pressão).
Substância
água
álcool etílico (anidro)
acetona
querosene
Nujol (óleo laxante)
Bálsamo do Canadá
Índice de refração (n)
1,333
1,362
1,357
1,448
1,477
1,537
REFLEXÃO E REFRACÃO RAIOS
Os raios incidente e refletido e a normal a superfície no ponto de
incidência pertencem ao mesmo plano e tem-se:
1 = 3
Reflexão
Refração
Os raios incidente e refratado e a normal a superfície no ponto
de incidência pertencem ao mesmo plano e tem-se:
1 1 = 2 2
2
30/05/2014
INTRODUÇÃO
O estudo das lentes esféricas, talvez seja dentre todas as
aplicações da óptica geométrica, a que mais se destaca pelo seu
uso no cotidiano como por exemplo em lentes de óculos ou
lupas em equipamentos de pesquisa astronômica, em câmeras
digitais e em microscópios.
Definimos lente esférica como o sistema óptico constituído de
três meios homogêneos e transparentes, separados dois a dois
por duas superfícies esféricas ou uma superfície esférica e uma
superfície plana, as quais chamamos faces da lente.
Para um estudo simples consideraremos que o segundo meio é
a lente propriamente dita, e que o primeiro e terceiro meios
são iguais.
TEORIA
3
30/05/2014
ELEMENTOS GEOMETRICOS DE UMA LENTE
C1 e C2: Centro de curvatura das faces da lente;
R1 e R2: Raios de curvatura das faces da lente;
Eixo principal: reta comum aos centros de curvatura
Vértices V1 e V2 das faces: interseção do eixo principal com as faces;
Espessura (e) da lente: distância entre os vértices.
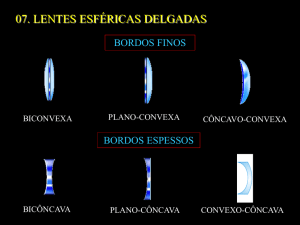
FORMA DAS LENTES
As lentes esféricas podem ser classificadas em:
Plano-convexa
Plano-côncava
biconvexa
Côncavo-convexa
Lentes de bordas
finas
bicôncava
Convexo-côncava
Lentes de
bordas grossas
4
30/05/2014
COMPORTAMENTO DAS LENTES
Lentes Esféricas
Convergentes
Lentes Esféricas
Divergentes
Convergência ou divergência de superfícies refratoras esféricas
1 1 = 2 2
Se o meio de incidência tem índice de difração inferior ao do meio para
onde se da a refração, então uma superfície convexa é convergente e
uma côncava é divergente (diagramas da linha de cima).
Se a relação de ordem entre os índices for a inversa, então as superfícies
convexas são divergentes e as côncavas são convergentes (diagramas da
linha de baixo).
5
30/05/2014
COMPORTAMENTO DAS LENTES
n da lente > n do meio
n da lente < n do meio
FOCOS PRINCIPAIS DE UMA LENTE DELGADA
Considere vários feixes de luz monocromática paralelo ao eixo
principal da lente. Ao ser refratado:
Se a lente for convergente, a luz
emergente converge para um
ponto,.
Se a lente for divergente, a luz
diverge em um ponto.
Este ponto do eixo principal, em relação ao qual a luz converge
ou diverge, é chamado foco principal imagem (Fi).
6
30/05/2014
FOCOS PRINCIPAIS DE UMA LENTE DELGADA
Agora, considere vários feixes de luz monocromática incidentes
de modo que os feixes emergentes sejam paralelos ao eixo
principal.
O ponto define o foco objeto da
lente convergente.
O ponto define o foco objeto
da lente divergente.
RESUMO DOS FOCOS PRINCIPAIS DE UMA LENTE
Resumindo, uma lente esférica apresenta dois focos principais:
o foco principal objeto (Fo) e o foco principal imagem (Fi).
7
30/05/2014
CENTRO ÓPTICO
O centro óptico é encontrado pela
intersecção da lente com o eixo óptico.
O raio de luz que passa pelo centro
óptico, ao ser refratado, não sofre
desvio angular nem lateral. Uma reta
que passe pelo centro óptico O é
chamada de eixo secundário.
DISTÂNCIA FOCAL
A distância entre o centro
óptico e um foco principal
de uma lente é chamada de
distância focal (f).
PONTOS ANTIPRINCIPAIS
A uma distância igual ao dobro da distância focal do eixo óptico
da lente, sobre o eixo principal, encontram-se dois pontos
notáveis de uma lente esférica: são os pontos antiprincipais. Um
raio de luz incidente numa lente esférica que passe (ou o seu
prolongamento) sobre o ponto antiprincipal objeto é refratado
passando (ou seu prolongamento) pelo ponto antiprincipal
imagem.
O
Ai
Fi
Fo
Ao
8
30/05/2014
RAIOS DE LUZ NOTAVEIS
Todo raio de luz que incide paralelamente ao eixo, é refratado na direção
do foco imagem.
O
Ai
Fi
Fo
Ao
Todo raio de luz que incide na direção do foco objeto, é refratado
paralelamente ao eixo
RAIOS DE LUZ NOTAVEIS
Todo raio de luz que incide na direção do centro óptico, é refratado sem
sofrer desvio na sua direção de propagação.
O
O
Ao
Fo
Fi
Ai
Ai
Fi
Fo
Ao
Todo raio de luz que incide na direção do ponto antiprincipal objeto, é
refratado na direção do ponto antiprincipal imagem
O
O
Ao
Fo
Fi
Ai
Ai
Fi
Fo
Ao
9
30/05/2014
CONSTRUÇÃO DA IMAGENS DAS LENTES
Considere um objeto extenso, luminoso
ou iluminado que é colocado
perpendicularmente ao eixo principal de
uma lente esférica. Para determinar a
imagem
desse
corpo,
devemos
encontrar a imagem do ponto A e a do
ponto B. Para determinarmos a imagem
do ponto A, utilizamos duas das
propriedades apresentadas no item
anterior. Já a imagem do ponto B, que
está situada no eixo principal, pode ser
determinada por uma perpendicular ao
eixo principal que passa pela imagem do
ponto A, uma vez que o objeto foi
colocado perpendicularmente sobre o
eixo principal. Assim, considerando
apenas objetos reais:
CONSTRUÇÃO DA IMAGENS DAS LENTES
Objeto real colocado no ponto antiprincipal
objeto.
Objeto real colocado entre o antiprincipal objeto
(Ao) e o foco objeto (Fo).
10
30/05/2014
CONSTRUÇÃO DA IMAGENS DAS LENTES
Objeto real colocado sobre o foco
principal objeto (Fo).
Objeto real colocado entre o foco principal
objeto (Fo) e o centro óptico (O).
CONSTRUÇÃO DA IMAGENS DAS LENTES
Objeto real colocado antes do
centro óptico (O) da lente
Observação:
Valido para lentes convergentes: A
imagem real de um objeto real é
invertida,
Valido para lentes divergentes: e a
imagem virtual de um objeto real é
direita.
11
30/05/2014
CONVENÇÃO DE SINAIS
Fo > 0 → lente convergente;
Fo < 0 → lente divergente;
Distância Objeto > 0 → objeto real;
Distância Objeto < 0 → objeto virtual;
Distância Imagem > 0 → imagem real;
Distância Imagem < 0 → imagem virtual;
Altura da Imagem > 0 → imagem direita;
Altura da Imagem < 0 → imagem inverFda
EQUAÇÃO PARA LENTES DELGADAS
1 1 1
= +
APLICAÇÕES
12
30/05/2014
MAQUINA FOTOGRÁFICA OU OLHO HUMANO
Objeto além do
ponto antiprincipal
objeto.
OBSERVAÇÃO: Imagem real, invertida e menor, situada entre o foco e o
ponto antiprincipal .
OLHO HUMANO
Formação da imagem em um olho
13
30/05/2014
A LUPA
É uma simples lente convergente que de um objeto real forma uma
imagem virtual, direita e maior.
Observe: Para visualizar a imagem
maior, o objeto deve estar entre a lente
e o ponto focal da lente.
LUNETAS
14
30/05/2014
COPIADORAS
EXERCÍCIOS
15
30/05/2014
ATIVIDADE EXPERIMENTAL
EXPERIMENTO 1 – DETERMINAÇÃO DA DISTÂNCIA FOCAL DE DUAS LUPAS
Determinação de f – usando o método dos pontos conjugados
1 1 1
= +
Determinação de f – usando o método de Bessel
Pode-se comprovar que para uma
distancia fixa A entre o objeto e o
anteparo, existem duas posições 1 e 2
da lente que produzem uma imagem
nítida do objeto sobre o anteparo.
Denominando-se D a distancia entre as
duas posições da lente, pode-se
comprovar que:
2 − 2
=
4
16
30/05/2014
EXPERIMENTO 2 – EXPERIMENTO COM OS OLHOS
PROCEDIMENTO
O tamanho da imagem na retina do observador é proporcional ao
ângulo θolho.
Para pequenos ângulos, θolho = ho/do
Faça com que o objeto pequeno se aproxime lentamente a seu olho (com
o outro fechado). Desta forma está mudando a distância do. Encontre do
de modo que a imagem comece a ficar desfocada. Então, estaremos
encontrando a distancia do, distancia próximo ao alho, onde para
menores valores de do, o olho não pode focalizar uma imagem.
EXPERIMENTO 2 – EXPERIMENTO COM A LUPA
PROCEDIMENTO
• Sem usar alguma fonte, monte uma lupa como mostrado na figura.
Faça esta atividade com os dois tipos de lentes de distancia focal 125
mm e 250 mm. Para cada lente, ajuste a distancia entre o objeto e
(acessório anteparo) e a lente para que a ampliação máxima a
imagem esteja claramente focalizada na retina.
17
30/05/2014
QUESTÕES
1) A equação fundamental dos lentes impõe limites na ampliação
que uma lente pode produzir?
2) Das duas lentes, para qual lente parece haver maior ampliação?
3) Calcule a ampliação angular para as lentes de distancia focal 125
mm e 250 mm? Seus cálculos são consistentes com a sua resposta
da questão 1?
4) Uma lente convergente com distancia focal de 50 mm seria útil
como uma lupa? Explique.
EXPERIMENTO 3 – MONTAGEM DE UM TELESCOPIO
PROCEDIMENTO
1. Utilizando a figura calcule tanθ1 e tanθ2 como uma função do tamanho da
imagem h1 e da distancia focal das duas lentes (f1 e f2). Sugestão:
considere θ1 e θ2 muitos pequenos, de modo que podem ser igualados a
tangente do ângulo.
2. Considerando que a ampliação angular do telescópio é definido como θ2 /
θ1 mostre que, em função das distancias focais, ela pode ser escrita
como.
1
= − = −
2
Observe que θ’1 é aprox. igual a
θ1 mostre
18
30/05/2014
2. Monte um telescópio usando as lentes de distancias focais 125 mm e
250 mm. A distancia entre as lentes será de aproximadamente 375
mm. Usando como a lente de 125 mm como ocular, observe alguns
objetos distantes. Ajuste a distancia entre as lentes se for necessário
para trazer o objeto para uma focalização melhor.
3. Para medir a ampliação, olhe por um olho através do telescópio e
com outro olhe diretamente para o objeto. Compare o tamanho das
imagens. Se a régua graduada for usada como objeto, poderão ser
feitas medidas bastante precisas da ampliação.
4. Qual a ampliação do telescópio quando é usada uma lente de 125
mm como ocular e de 250 mm como objetiva.
5. Qual é a ampliação do telescópio se as lentes forem trocadas de
posição?
6. Suas respostas para as questões 3 e 4 estão de acordo com os valores
da questão 2?
7. Explique porque a distancia entre as lentes deve ser
aproximadamente igual à soma das suas distancias focais?
+ 250 mm
+ 125mm
+ 375 mm
Figura. Disposição das componentes para a montagem de um
telescópio
19
30/05/2014
EXPERIMENTO 4 – MONTAGEM DE UM MICROSCÓPIO
O microscópio utiliza duas lentes para obter maior ampliação dos
objetos próximos e é maior que aquela imagem obtida com uma
lupa. Mostra-se o diagrama ótico na seguinte figura.
Figura. Formação de uma imagem num microscópio. A lente objetiva L1
funciona como um projetor. O objeto é colocado alem do ponto focal L1, assim
como uma imagem real invertida e aumentada é formada. A ocular L2 funciona
como uma lupa. Ela forma uma imagem virtual e aumentada da imagem real
formada por L1.
PASSOS
1. Monte o microscópio como mostrado na figura. Use a lente de
distancia 125 mm como lente objetiva e a de distancia focal
250 mm como lente ocular. Posicione o objeto a uma distancia
qualquer na região f1<do<2f1 em relação a lente objetiva.
2. Coloque o anteparo entre as lentes, procurando uma posição
onde a formação de imagem intermediaria.
3. Meça a distancia entre o anteparo e a lente objetiva. Retire o
anteparo e ajuste a posição da ocular até que você veja uma
imagem clara do objeto.
4. Meça a distancia entre os lentes.
+ 125mm
+ 250 mm
20
30/05/2014
5. A imagem é ampliada? Pode comparar esta ampliação com a da lupa
de 125mm?
6. Porque a ampliação aumenta se a lente objetiva estiver mais próxima
do objeto?
7. Quais problemas de focalização ocorrem com o aumento da
ampliação?
8. Qual o efeito da abertura na focalização?
9. Qual o efeito da abertura sobre o brilho da imagem?
10. Que vantagem haveria em se usar uma lente de distancia focal 125
mm como ocular mantendo a de 250 mm como objetiva?
21