PARTE A: - Uniposrio

EXAME UNIFICADO DAS PÓS-GRADUAÇÕES EM FÍSICA DO RIO DE JANEIRO
Primeiro Semestre de 2013 - 09 de novembro de 2012
AS 4 QUESTÕES DA PARTE A SÃO OBRIGATÓRIAS.
ESCOLHA 2, E APENAS 2, QUESTÕES DA PARTE B.
A PROVA TEM DURAÇÃO MÁXIMA DE 4 HORAS. BOA PROVA.
PARTE A:
Problema 1:
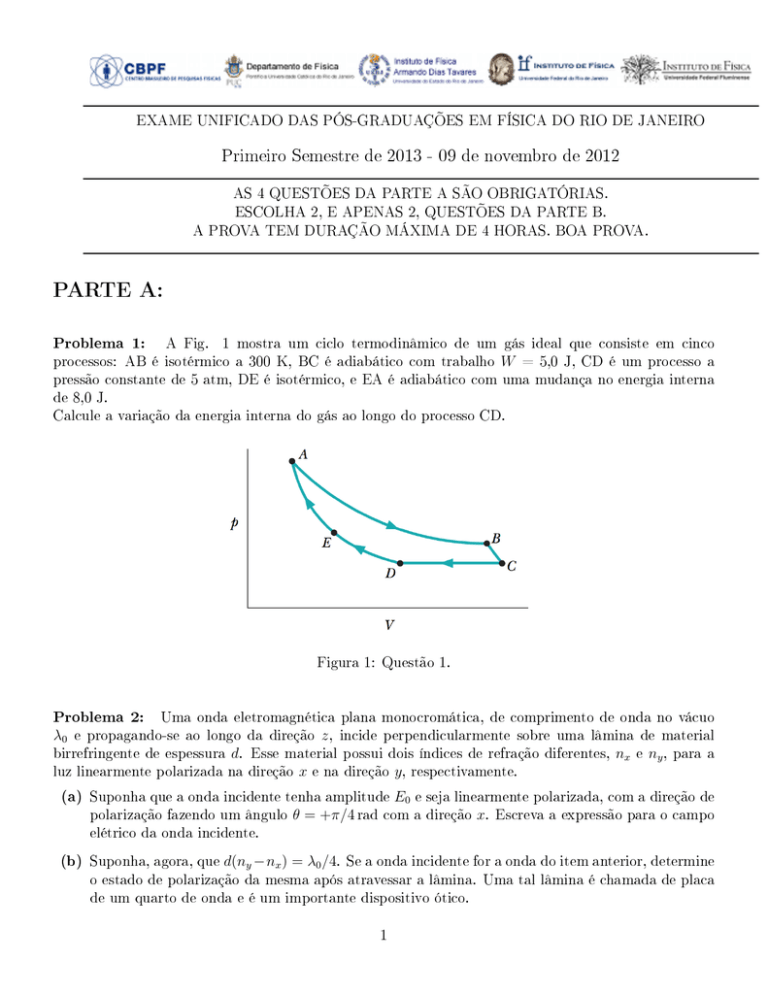
A Fig.
1 mostra um ciclo termodinâmico de um gás ideal que consiste em cinco
processos: AB é isotérmico a 300 K, BC é adiabático com trabalho
W
= 5,0 J, CD é um processo a
pressão constante de 5 atm, DE é isotérmico, e EA é adiabático com uma mudança no energia interna
de 8,0 J.
Calcule a variação da energia interna do gás ao longo do processo CD.
Figura 1: Questão 1.
Problema 2:
λ0
Uma onda eletromagnética plana monocromática, de comprimento de onda no vácuo
e propagando-se ao longo da direção
birrefringente de espessura
d.
incide perpendicularmente sobre uma lâmina de material
Esse material possui dois índices de refração diferentes,
luz linearmente polarizada na direção
(a)
z,
x
e na direção
Suponha que a onda incidente tenha amplitude
polarização fazendo um ângulo
θ = +π/4 rad
y,
E0
nx
e
ny ,
para a
respectivamente.
e seja linearmente polarizada, com a direção de
com a direção
x.
Escreva a expressão para o campo
elétrico da onda incidente.
(b)
Suponha, agora, que
d(ny −nx ) = λ0 /4.
Se a onda incidente for a onda do item anterior, determine
o estado de polarização da mesma após atravessar a lâmina. Uma tal lâmina é chamada de placa
de um quarto de onda e é um importante dispositivo ótico.
1
Problema 3:
q está uniformemente distribuída sobre um anel circular de raio r e espessura
o eixo de simetria do anel coincida com o eixo z .
Uma carga
desprezível. Suponha que
(a)
Determine o campo elétrico gerado pelo anel a uma distância
(b)
Mostre que quando
z >> r
(c)
k̂
do centro.
o campo pode ser aproximado por:
~
E(z)
≈
onde
z
é um vetor unitário na direção
q 1
4πε0 z 2
3 r2
1−
2 z2
k̂ ;
z.
Interprete o primeiro termo da série (a saber,
q/4πε0 z 2 ).
Problema 4:
na
altura
de
raio
Um disco uniforme de massa M e raio r rola sem deslizar, começando do repouso
H + r como na gura 2 pelo plano inclinado, e após atingir a horizontal, realiza um loop
R = 2r, se possível. Dado: Icm = 21 M r2
Loop
R
H+ r
Figura 2: Questão 4.
(a)
Calcule a energia cinética total
do centro de massa
(b)
no trecho horizontal e
KL
no loop, como função da velocidade
Calcule a velocidade do centro de massa do disco no ponto mais alto do loop, em função de
R
(c)
KH
vCM .
e
H,
g.
Calcule a velocidade mínima que o disco precisa ter no ponto mais alto do loop para que não
descole do mesmo.
(d)
Conclua o problema calculando a altura mínima
2
Hmin para que o disco faça o loop
com segurança.
PARTE B: Lembre-se de escolher 2, e apenas 2, problemas desta
parte.
Problema 5:
da camada
No seu estado fundamental, o tamanho do átomo de hidrogênio pode ser dado pelo raio
2
2
isto é, a0 = 4π~ ε0 /(µe ) ' 0.5Å (µ é a massa reduzida do átomo de hidrogênio e e é
n = 1,
a carga do elétron). Mostre que essa dimensão atômica básica pode ser obtida diretamente do príncipio
de incerteza.
Problema 6:
Considere o operador
d
, no qual φ é a coordenada polar usual em duas dimensões.
Q̂ ≡ i dφ
(a)
Mostre que
(b)
Encontre suas autofunções e seus autovalores.
Q̂
é hermitiano.
[Suponha que a autofunção
Problema 7:
f
obedece a propriedade
f (φ + 2π) = f (φ)]
Uma partícula é representada pela função de onda normalizada abaixo:
( q
Ψ(x) =
15
(a2
16a5
− x2 )
0
se
se
−a < x < a;
x ≥ a ou x ≤ −a.
(1)
(a)
Determine a incerteza na posição desta partícula.
(b)
Determine a incerteza no momento desta partícula.
(c)
Os resultados obtidos nos itens (a) e (b) são compatíveis com o princípio da incerteza? Justique.
Problema 8:
Um elétron está no seguinte estado de spin:
χ = A
1 − 2i
2
,
onde o estado acima foi escrito na base dos auto-estados de
(a)
(b)
Determine a constante de normalização
Se
Sz
Se
Sx
A.
for medido neste elétron quais valores poderão ser obtidos com quais probabilidades? Qual
é o valor esperado de
(c)
Sz .
Sz ?
for medido neste elétron quais valores poderão ser obtidos com quais probabilidades?
σx =
0 1
1 0
,
σy =
0 −i
i 0
3
,
σz =
1 0
0 −1
EXAME UNIFICADO DAS PÓS-GRADUAÇÕES EM FÍSICA DO RIO DE JANEIRO
th
First Semester de 2013 - November 9
, 2012
YOU MUST SOLVE ALL 4 PROBLEMS FROM PART A.
CHOOSE 2, AND ONLY 2, PROBLEMS FROM PART B.
YOU CAN USE UP TO 4 HOURS TO SOLVE THE EXAM. HAVE A GOOD EXAM.
PART A:
Problem 1:
Fig. 1 shows an ideal gas cycle consisting of ve paths: AB is isothermal at 300 K, BC
is adiabatic with work
W
= 5.0 J, CD is performed at a constant pressure of 5 atm, DE is isothermal,
and EA is adiabatic with a change in internal energy of 8.0 J. What is the change in internal energy of
this ideal gas along path CD?
Figure 1: Problem 1.
Problem 2:
along the
z
A plane monochromatic electromagnetic wave of wavelength
material possesses two dierent indices of refraction,
y
λ0
in vacuum, propagating
d. The
the x and
direction, impinges perpendicularly on a plate of birefringent material of thickness
nx
and
ny ,
for linearly polarized light in
directions, respectively.
(a)
Suppose that the incident wave has amplitude
θ = +π/4 rad
(b)
with the
Suppose now that
x
E0
and is linearly polarized at an angle of
direction. Write the expression for its electric-eld vector.
d(ny − nx ) = λ0 /4.
If the incident wave is the wave of the previous item,
determine its polarization state when emerging from the plate. Such a plate is called a quarterwave plate and is an important optical element.
1
Problem 3:
q is uniformly distributed over a circular ring of radius r and negligible thickness.
axis coincides with the z axis.
A charge
Assume its symmetry
(a)
Determine the electric eld generated by this ring at a distance
(b)
Show that when
z >> r
(c)
k̂
is a unit vector in the
z
q 1
4πε0 z 2
3 r2
1−
2 z2
k̂ ;
direction.
Interpret the rst term of the series (to wit,
Problem 4:
from the center.
the eld can be approximated by:
~
E(z)
≈
where
z
An uniform disc of mass
M
q/4πε0 z 2 ).
and radius
r
rolls without sliding, starting at rest from
as shown in the gure 2, and goes around the loop, of radius
1
2
is Icm = M r .
2
R = 2r,
H +r
if possible. Its moment of inertia
Loop
R
H+ r
Figure 2: Problem 4.
(a)
Calculate the total kinetic energy
the velocity of the center of mass
(b)
KH at
vcm .
the horizontal plane and
KL
at the loop as a function of
Calculate the velocity of the center of mass of the disc at the highest point of the loop as a function
of
H, R
and
g.
(c)
Calculate the minimum velocity of the disc necessary to go around the loop without losing contact.
(d)
Conclude the problem by obtaining the minimum initial height
do the loop.
2
Hmin
so that the disc can safely
PART B: Remember to choose 2, and only 2 problems from this
part.
Problem 5:
shell, i.e.
In its ground state the size of the hydrogen atom can be given by the radius of the n = 1
a0 = 4π~2 ε0 /(µe2 ) ' 0.5Å (µ is the reduced mass of the hydrogen atom and e the charge of the
electron). Show that this basic atomic scale can be obtained directly from the uncertainty principle.
Problem 6:
Consider the operator
d
,
Q̂ ≡ i dφ
(a)
Show that
(b)
Find its eigenfunctions and eigenvalues.
Q̂
φ
is the usual polar coordinate in two dimensions.
is hermitian.
[Assume that the eigenfunction
Problem 7:
where
f
obey the property
f (φ + 2π) = f (φ)]
A particle is represented by the following normalized wave function
( q
Ψ(x) =
15
(a2
16a5
− x2 )
0
se
se
−a < x < a;
x ≥ a ou x ≤ −a.
(a)
Determine the uncertainty in the position of this particle.
(b)
Determine the uncertainty in the momentum of this particle.
(c)
Are the results obtained in items (a) and (b) compatible with the uncertainty principle? Justify.
Problem 8:
One electron is at the following spin state:
χ = A
1 − 2i
2
,
where the state above was written in a basis of the eigenvalues of
(a)
Determine the normalization constant
(b)
If
Sz
If
Sx
A.
is measured for this electron, which values can be obtained and with which probabilities?
What is the expected value of
(c)
Sz .
Sz ?
is measured for this electron, which values can be obtained and with which probabilities?
σx =
0 1
1 0
,
σy =
0 −i
i 0
3
,
σz =
1 0
0 −1