Plano de Ensino

Ministério da Educação
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Campus Pato Branco
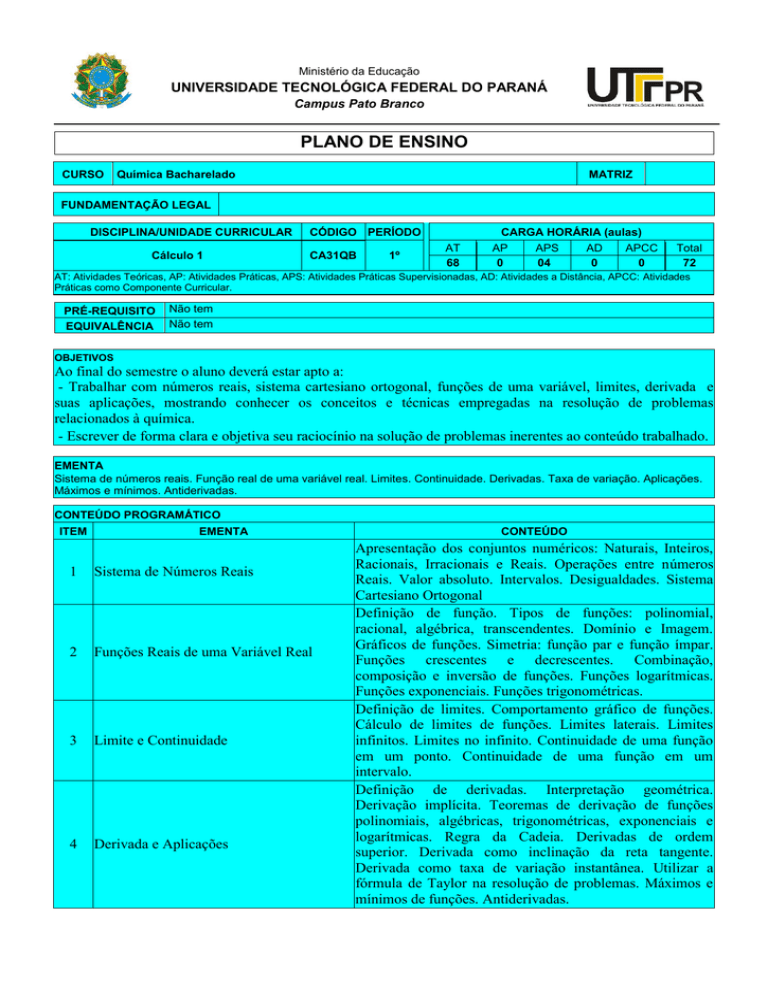
PLANO DE ENSINO
CURSO
Química Bacharelado
MATRIZ
FUNDAMENTAÇÃO LEGAL
DISCIPLINA/UNIDADE CURRICULAR
Cálculo 1
CÓDIGO PERÍODO
CA31QB
1º
AT
68
CARGA HORÁRIA (aulas)
AP
APS
AD
APCC
0
04
0
0
Total
72
AT: Atividades Teóricas, AP: Atividades Práticas, APS: Atividades Práticas Supervisionadas, AD: Atividades a Distância, APCC: Atividades
Práticas como Componente Curricular.
PRÉ-REQUISITO
EQUIVALÊNCIA
Não tem
Não tem
OBJETIVOS
Ao final do semestre o aluno deverá estar apto a:
- Trabalhar com números reais, sistema cartesiano ortogonal, funções de uma variável, limites, derivada e
suas aplicações, mostrando conhecer os conceitos e técnicas empregadas na resolução de problemas
relacionados à química.
- Escrever de forma clara e objetiva seu raciocínio na solução de problemas inerentes ao conteúdo trabalhado.
EMENTA
Sistema de números reais. Função real de uma variável real. Limites. Continuidade. Derivadas. Taxa de variação. Aplicações.
Máximos e mínimos. Antiderivadas.
CONTEÚDO PROGRAMÁTICO
ITEM
EMENTA
1
Sistema de Números Reais
2
Funções Reais de uma Variável Real
3
Limite e Continuidade
4
Derivada e Aplicações
CONTEÚDO
Apresentação dos conjuntos numéricos: Naturais, Inteiros,
Racionais, Irracionais e Reais. Operações entre números
Reais. Valor absoluto. Intervalos. Desigualdades. Sistema
Cartesiano Ortogonal
Definição de função. Tipos de funções: polinomial,
racional, algébrica, transcendentes. Domínio e Imagem.
Gráficos de funções. Simetria: função par e função ímpar.
Funções crescentes e decrescentes. Combinação,
composição e inversão de funções. Funções logarítmicas.
Funções exponenciais. Funções trigonométricas.
Definição de limites. Comportamento gráfico de funções.
Cálculo de limites de funções. Limites laterais. Limites
infinitos. Limites no infinito. Continuidade de uma função
em um ponto. Continuidade de uma função em um
intervalo.
Definição de derivadas. Interpretação geométrica.
Derivação implícita. Teoremas de derivação de funções
polinomiais, algébricas, trigonométricas, exponenciais e
logarítmicas. Regra da Cadeia. Derivadas de ordem
superior. Derivada como inclinação da reta tangente.
Derivada como taxa de variação instantânea. Utilizar a
fórmula de Taylor na resolução de problemas. Máximos e
mínimos de funções. Antiderivadas.
PROFESSOR
TURMA
Renan Henrique Martins
1QB
ANO/SEMESTRE
2014/02
AT
68
CARGA HORÁRIA (aulas)
APS
AD
4
0
AP
0
APCC
0
Total
72
AT: Atividades Teóricas, AP: Atividades Práticas, APS: Atividades Práticas Supervisionadas, AD: Atividades a Distância, APCC: Atividades
Práticas como Componente Curricular.
DIAS DAS AULAS PRESENCIAIS
Dia da semana
Segunda
Número de aulas no semestre
Terça
38
Quarta
-
Quinta
-
Sexta
30
Sábado
-
PROGRAMAÇÃO E CONTEÚDOS DAS AULAS (PREvisão)
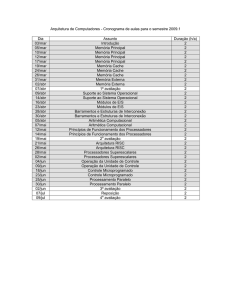
Dia/
01/mar
04/mar
08/mar
11/mar
15/mar
18/mar
22/mar
29/mar
01/abr
05/abr
08/abr
12/abr
15/abr
19/abr
26/abr
29/abr
03/mai
06/mai
10/mai
13/mai
17/mai
19/mai
24/mai
31/mai
03/jun
07/jun
10/jun
14/jun
17/jun
21/jun
24/jun
28/jun
01/jul
05/jul
Conteúdo das Aulas
Apresentação do plano de ensino. Números reais.
Operações com números reais. Operações inversas.
Desigualdades. Valor absoluto.
Funções: conceito e exemplos.
Gráficos de funções.
Propriedades de funções.
Função do 1° grau, modular, constante, identidade.
Função quadrática. Funções polinomiais.
Função exponencial e logarítmica.
Funções trigonométricas.
Função composta. Funções Inversas.
Avaliação
Limites: noção intuitiva. Limites laterais.
Limites: propriedades e estratégias de resolução (fatoração, divisão de Briott Rufini,
multiplicação pelo conjugado...)
Limites: propriedades e estratégias de resolução (fatoração, divisão de Briott Rufini,
multiplicação pelo conjugado...)
Continuidade de funções
Limites tendendo ao infinito -assíntotas horizontais.
Limites especiais (trigonométricas e exponenciais)
Teorema do confronto.
Avaliação
Derivadas: definição algébrica e geométrica.
Propriedades de derivadas.
Derivadas de funções polinomiais.
Derivadas de exponenciais e logarítmicas.
Derivadas de trigonométricas.
Regra da cadeia.
Derivada de inversas.
Aplicações.
Aplicações.
Aplicações.
Avaliação
Vista da Avaliação e Revisão
Exame
Vsita do Exame
Número
de Aulas
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
68
PROCEDIMENTOS DE ENSINO
AULAS TEÓRICAS
Aula expositiva dialogada e com a utilização de recursos didáticos como multimídia, etc.
ATIVIDADES PRÁTICAS SUPERVISIONADAS
As Atividades Práticas Supervisionadas (APS) serão compostas de três listas de exercícios referentes a cada avaliação.
PROCEDIMENTOS DE AVALIAÇÃO
Prova escrita
As avaliações serão compostas por três provas individuais e sem consulta, no valor de 100% da nota e distribuídas ao longo do
semestre, conforme explicitado na tabela de conteúdos acima. Cada uma das avaliações será composta de uma prova escrita com
peso 10,0. A média parcial de semestre (MP) será a média aritmética dessas provas. O aluno com freqüência inferior a 75% será
considerado reprovado na disciplina, já o aluno com média inferior a 6,0 terá direito a prestar exame final (EF) que substituirá a
menor nota no semestre. Aluno com média superior ou igual a 6,0 será considerado aprovado. Ao final do semestre o aluno terá a
oportunidade de realizar uma avaliação substitutiva referente à uma das avaliações realizadas durante o semestre. Nos casos em
que o discente não comparecer a alguma das provas, a avaliação de segunda chamada será ofertada somente no final do semestre,
no dia da avaliação substitutiva, mediante requerimento deferido pela secretaria.
O exame final será uma prova escrita envolvendo o conteúdo de todo o programa da disciplina. O aluno com exame será
considerado aprovado se tiver média final (MF) superior ou igual a 6,0. Definida por MF=(M1+M2+M3)/3.
REFERÊNCIAS
Referências Básicas:



STEWART, J. Cálculo. Vol. 1. Cengage Learning. 6.a ed. 2009.
ANTON, H.; BIVENS, I.; DAVIS, S. Cálculo. Trad. Ivo Doering. 8. ed. v. 1. Porto Alegre: Bookman, 2007.
THOMAS, G. B. Cálculo. Vol. 1. Pearson. 10.a ed. 2002.
Referências Complementares:





LEITHOLD, L. Cálculo com geometria analítica. Vol. I, São Paulo: Harbra, 1994.
GUIDORIZZI, H. L. Um curso de cálculo, 5. ed. Vol. I, São Paulo: LTC - Livros Técnicos e Científicos Editora S. A., 2001.
ÁVILA, Geraldo. Cálculo. 6. ed. Rio de Janeiro: LTC, 1994. 3 v. (v.1)
HOFFMANN, Laurence D.. Cálculo: um curso moderno e suas aplicações. 2.ed. Rio de Janeiro: LTC, 1990. 2 v.
SWOKOWSKI, E. W. Cálculo com geometria analítica. 2. ed. Vol. I, São Paulo: Makrow Books, 1994.
ORIENTAÇÕES GERAIS
Carga horária da disciplina integralizada através da utilização de Atividades Práticas Supervisionadas.
Assinatura do Professor
Assinatura do Coordenador do Curso