Universidade Nova de Lisboa
Faculdade de Ciências e Tecnologia
Secção de Electrotecnia e Máquinas Eléctricas
Máquina Síncrona em Regime Transitório
após Brusco Curto-Circuito no Estator
por
João Leal Fernandes
Dissertação apresentada na Faculdade de Ciências e Tecnologia da Universidade Nova
de Lisboa para obtenção do grau de Mestre em Engenharia Electrotécnica e de
Computadores.
Orientador científico:
Prof. Doutor Amadeu Leão Rodrigues
Lisboa, 2006
i
Agradecimentos
Quero antes de mais expressar a minha gratidão ao Prof. Doutor Amadeu Leão
Rodrigues pela disponibilidade demonstrada no decorrer do trabalho e todo apoio prestado.
Agradecimento à minha empresa Delphi Automotive Systems – Portugal S.A., por me ter
possibilitado a inscrição no Mestrado de Engenharia Electrotécnica e de Computadores ao
abrigo do protocolo existente entre as duas instituições. De destacar ainda, o facto de a Delphi
ter facilitado a utilização de instrumentação de medida, através da qual foi possível extrair os
elementos fundamentais para a realização deste trabalho.
Agradeço ao Departamento de Engenharia Electrotécnica da Faculdade de Ciências e
Tecnologia da Universidade Nova de Lisboa o facto de ter tido à disposição as excelentes
condições do Laboratório de Máquinas Eléctricas que foram determinantes para a realização
deste trabalho.
Aos professores que me sensibilizaram para área de Máquinas Eléctricas, no decorrer dos
meus estudos no Instituto Politécnico de Setúbal, Doutor Manuel Gaspar e Doutor Jorge
Esteves.
Finalmente quero agradecer à minha mulher que me soube transmitir uma palavra de
força e coragem para ultrapassar algumas dificuldades encontradas durante o tempo de
elaboração deste trabalho.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
ii
Sumário
Sumário em Português.
A partir das equações de Park pretende-se modelar a máquina de rotor de pólos
salientes com enrolamentos amortecedores e prever o seu funcionamento em regime
transitório.
A dissertação tem como objectivo estabelecer a teoria generalizada da máquina
síncrona em regime transitório e proceder a ensaios laboratoriais a fim de obter as correntes
de curto-circuito trifásico simétrico, difásico e fase-neutro. A partir destes ensaios é possível
obter as constantes de tempo e reactâncias transitórias e subtransitórias do alternador, cujo
conhecimento é importante para o dimensionamento dos disjuntores de protecção do
alternador e toda a carga a jusante.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
iii
Abstract
From Park equations is intended to create the machine model of salient pole rotor with
damping windings and to foresee its running in transitory regime.
The objective of the dissertation is to establish the generalized theory of the synchronous
machine in transitory regime and to perform the laboratorial experiments in order to get the
short circuit symmetrical currents, phase to phase and phase to neutral. From these study it is
possible to get the transitory time constants and transitory reactances of the machine.
The knowledge of these constants is very important for the design of the protections of
the alternator.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
iv
Dedicatória
Esta dissertação é dedicada à minha mulher e aos meus filhos, que ficaram privados
da minha presença ao longo de muitas horas para que este trabalho pudesse ser uma
realidade.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
v
Simbologia e Notações
Lista contendo símbolos e notações usados ao longo da dissertação.
f - frequência da rede.
ra - Resistência de dispersão do estator (armadura).
rf - Resistência de dispersão do enrolamento do campo (rotor).
uf - Tensão de alimentação do enrolamento de campo.
rkd - Resistência do enrolamento amortecedor eixo directo.
rkq - Resistência do enrolamento amortecedor eixo quadratura.
[Hz]
[Ω]
[Ω]
[V]
[Ω]
[Ω]
- Reactância do enrolamento de campo
- Reactância Síncrona
- Reactância Síncrona do enrolamento do eixo directo.
- Reactância Síncrona do enrolamento do eixo directo.
[Ω]
[Ω]
[Ω]
[Ω]
X q - Reactância Síncrona do enrolamento do eixo quadratura.
[Ω]
Xf
X+
Xd
Xd
X 'd
- Reactância Transitória do enrolamento do eixo directo.
[Ω]
X 'q
- Reactância Transitória do enrolamento do eixo quadratura.
[Ω]
X ''d
- Reactância Subtransitória do enrolamento do eixo directo.
[Ω]
X ''q
- Reactância Subtransitória do enrolamento do eixo quadratura.
[Ω]
X kd
- Reactância do enrolamento amortecedor eixo directo.
[Ω]
X kq
- Reactância do enrolamento amortecedor eixo quadratura.
[Ω]
X md = ωLmd
- Resistência de magnetização do eixo directo.
X mq = ωX mq - Resistência de magnetização do eixo quadratura.
X f = ωlf
X kd = ωlkd
X kq = ωlkq
- Reactância de dispersão do campo (rotor).
- Reactância de dispersão do enrolamento amortecedor directo.
- Reactância de dispersão do enrolamento amortecedor quadratura.
X2 - Reactância de sequência negativa
X0 - Reactância de sequência zero
Ta - Constante de tempo na armadura
Td' - Constante de tempo transitória do enrolamento do eixo directo em
curto circuito.
'
- Constante de tempo transitória do enrolamento do eixo directo
Td0
em circuito aberto.
' - Constante de tempo transitória do enrolamento do eixo quadratura
Tq
em curto circuito.
'
Tq0 - Constante de tempo transitória do enrolamento do eixo quadratura
em circuito aberto.
'' - Constante de tempo subtransitória do enrolamento do eixo directo
Td
em curto circuito.
J.L.F. – Máquina Síncrona em Regime Transitório
[Ω]
[Ω]
[Ω]
[Ω]
[Ω]
[Ω]
[Ω]
[s]
[s]
[s]
[s]
[s]
[s]
2006
vi
''
- Constante de tempo subtransitória do enrolamento do eixo directo
Td0
em circuito aberto.
Tq'' - Constante de tempo subtransitória do enrolamento do eixo
quadratura em curto circuito.
Tq''0 - Constante de tempo subtransitória do enrolamento do eixo
quadratura em circuito aberto.
Tkd - Constante de tempo do enrolamento do eixo amortecedor eixo
directo.
Tkq - Constante de tempo do enrolamento do eixo amortecedor eixo
quadratura.
'' - Corrente Subtransitória do eixo directo
I
[s]
[s]
[s]
[s]
[s]
[A]
d
I d'
- Corrente Transitória do eixo directo
[A]
Id
- Corrente Síncrona do eixo directo
[A]
I q''
- Corrente Subtransitória do eixo quadratura
[A]
I q'
- Corrente Transitória do eixo quadratura
[A]
I q - Corrente Síncrona do eixo quadratura
Un
In
P
U exc
Iexc
cosϕ
N
f.m.m.
f.e.m.
P
ϕ
δ
Lq
[A]
- Tensão nominal de uma máquina.
- Corrente nominal de uma máquina.
[V]
[A]
- Potência Activa de uma máquina.
- Tensão de excitação de uma máquina.
- Corrente de excitação de uma máquina.
[W]
[V]
[A]
- Coeficiente de factor de potência.
- Velocidade de uma máquina em rotações por minuto.
- Força magneto-motriz
- Força electro-motriz
- Permeância magnética
[rpm]
[V]
[V]
- Ângulo de desfasamento entre tensão e corrente
- Ângulo de carga de uma máquina
- Indutância do enrolamento do eixo quadratura
Lmd - Indutância de magnetização do eixo directo
Lmq - Indutância de magnetização do eixo quadratura
[ Ω -1 ]
[º]
[º]
[H]
[H]
[H]
la
Lf
Lkd
- Indutância da armadura do estator
- Indutância do enrolamento de campo
- Indutância do enrolamento amortecedor do eixo directo
[H]
[H]
[H]
Lkq
- Indutância do enrolamento amortecedor do eixo quadratura
[H]
φR
- Fluxo magnético do rotor
[Wb]
J.L.F. – Máquina Síncrona em Regime Transitório
2006
vii
Índice
Pag.
Capítulo 1 – Breve Descrição Máquina Síncrona Trifásica ......................... 1
1.1 - Constituição da Máquina Síncrona Trifásica..................................................
1
1.1.1 - Máquina Síncrona com Rotor Cilíndrico.................................................
2
1.1.2 - Máquina Síncrona de Pólos Salientes......................................................
2
1.2 - Princípio de Funcionamento da Máquina Síncrona........................................
8
1.2.1 - Equação Vectorial da Máquina Síncrona de Rotor Cilíndrico.................
8
1.2.2 - Equação vectorial da Máquina Síncrona de Rotor de Pólos Salientes..... 13
1.2.3 - Variação da Reactância em Função da Posição do Rotor........................ 14
1.2.4 - Ensaio de Escorregamento para Determinação de Xd e Xq...................... 16
Capítulo 2 – Transformação de Park..................................................................
19
2.1 - Transformação do Sistema Trifásico em Sistema Bifásico.............................
19
Capítulo 3 – Equações Gerais da Máquina Síncrona.....................................
23
3.1 – Modelo da Máquina Síncrona de Pólos Salientes..........................................
23
Capítulo 4 – Constantes da Máquina Síncrona................................................
30
4.1 – Significado Físico dos Parâmetros da Máquina Síncrona..............................
4.1.1 - Período Sub-Transitório...........................................................................
4.1.2 - Período Transitório...................................................................................
4.1.3 - Regime Permanente.................................................................................
4.1.4 – Funcionamento do Enrolamento Amortecedor.......................................
4.2 – Análise do Modelo da Máquina.....................................................................
4.2.1 - Esquema Eléctrico da Máquina em Regime Subtransitório.....................
4.2.2 - Esquema Eléctrico da Máquina em Regime Transitório..........................
4.2.3 - Esquema Eléctrico da Máquina em Regime Permanente........................
30
30
32
32
33
34
34
37
39
Capítulo 5 – Equações da Máquina do Curto-Circuito..................................
40
5.1 - Equações das Reactâncias...............................................................................
5.1.1 – Reactância Síncrona................................................................................
5.1.2 – Reactância Transitória.............................................................................
5.1.3 – Reactância Subtransitória........................................................................
5.2 – Equações de Curto-Circuito Simétrico Trifásico em Vazio........................
5.2.1 - Equações das Correntes nas Fases a, b e d..............................................
5.2.2 - Equação da Corrente de Campo...............................................................
5.2.3 - Equação do Binário Resistente................................................................
5.3 - Curto-Circuito Trifásico Assimétrico Fase-Fase em Vazio............................
40
40
42
43
44
45
52
54
57
J.L.F. – Máquina Síncrona em Regime Transitório
2006
viii
5.3.1 - Equações das Correntes nas Fases...........................................................
5.3.2 – Equação das Corrente de Campo.............................................................
5.4 - Curto-Circuito Trifásico Assimétrico Fase-Neutro em Vazio........................
5.4.1 - Equações das Correntes na Fase e no Neutro..........................................
5.4.2 - Equação da Corrente de Campo...............................................................
5.5 - Curto-Circuito Trifásico Assimétrico Fase-Fase-Neutro em Vazio...............
5.5.1 – Equações das Correntes nas Fases...........................................................
5.5.2 - Equação da Corrente de Campo...............................................................
57
59
60
60
61
62
62
64
Capítulo 6 – Ensaios Laboratoriais.....................................................................
65
6.1 - Equipamento para o Ensaio no Laboratório...................................................
6.1.1 - Bancada de Ensaios.................................................................................
6.1.2 - Equipamento de Medida........................................................................
6.2 - Ensaio Experimental para Obtenção das Características em Vazio e CurtoCircuito....................................................................................................................
6.3 - Ensaio em Curto-Circuito Simétrico entre as Três Fases...............................
6.3.1 –Simulação de Cálculo das Correntes de Curto-Circuito...........................
6.4 - Ensaio em Curto-Circuito Assimétrico entre Duas Fases...............................
6.4.1 –Simulação de Cálculo das Correntes de Curto-Circuito...........................
6.5 - Ensaio em Curto-Circuito Assimétrico entre Fase e Neutro .........................
6.5.1 – Simulação de Cálculo das Correntes de Curto-Circuito..........................
65
65
66
67
70
72
84
89
93
97
Capítulo 7 – Comportamento Dinâmico do Alternador................................. 109
7.1 - Comportamento do Binário durante o Curto-Circuito.....................................
7.1.1 – Determinação dos Parâmetros Mecânicos...............................................
7.1.2 – Cálculo do Momento de Inércia do rotor.................................................
7.1.3 – Métodos para Determinar o Momento de Inércia....................................
109
110
110
112
Capítulo 8 – Conclusões Finais............................................................................ 114
Capítulo 9 – Trabalho Futuro...............................................................................
115
Capítulo 10 – Bibliografia....................................................................................... 116
Anexos .................................................................................................................
Anexo I – Tabelas de Resultados................................................................
Anexo II – Instrumentação de Medida......................................................
Anexo III – Fotografias da Bancada de Ensaios.....................................
Anexo IV – Curto-Circuito Simétrico........................................................
Anexo V – Curto-Circuito Assimétrico Fase-Fase.................................
J.L.F. – Máquina Síncrona em Regime Transitório
117
118
122
124
127
128
2006
ix
Anexo VI – Curto-Circuito Assimétrico Fase-Neutro........................... 129
Anexo VII – Curto-Circuito Assimétrico Fase-Fase-Neutro............... 130
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
Capítulo 1
1
Breve Descrição da Máquina
Síncrona Trifásica
1.1 - Constituição da máquina síncrona trifásica.
A máquina síncrona trifásica é constituída por três enrolamentos, cujos eixos magnéticos
estão desfasados de 120º eléctricos, que constituem o estator. No seu interior existe o rotor
que produz um fluxo magnético estático criado por um corrente continua (excitação).
Esta máquina como todas as máquinas eléctricas é reversível, isto é fornecendo energia
mecânica ao veio do rotor, colocando-o a rodar com uma velocidade angular ω esta máquina
converte a energia mecânica em energia eléctrica no estator (gerador ou alternador);
alternativamente, alimentando o estator com um sistema trifásico de tensões, fornecendolhe energia eléctrica a máquina converte-a em energia mecânica (motor) que surge no seu
veio.
a) Rotor cilíndrico
b) Rotor de pólos salientes
Fig. 1.1 - Máquina de rotor cilíndrico e máquina de rotor de pólos salientes
A máquina síncrona pode ser monofásica ou polifásica, bipolar ou tetrapolar (rotor
cilíndrico) ou multipolar (rotor de pólos salientes). Este trabalho visa o estudo da máquina
síncrona trifásica de pólos salientes e o seu comportamento em regime transitório.
O rotor, ou indutor, é constituído por um enrolamento alimentado por uma fonte de
tensão contínua exterior, equivalendo a um electromagneto. O rotor pode apresentar ainda
duas formas físicas distintas – rotor cilíndrico e rotor de pólos salientes. Como exemplo a
figura 1.1 a) mostra um rotor cilíndrico bipolar onde, o entreferro ao longo da periferia do
estator é constante. A figura 1.1 b) mostra um rotor com quatro pólos salientes, onde o
entreferro da máquina é variável ao longo da periferia do estator.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
2
1.1.1 - Máquina Síncrona com Rotor Cilíndrico
A forma física do rotor irá influenciar bastante as características da máquina.
O rotor cilíndrico é constituído por um núcleo de forma cilíndrica, em regra geral é
forjado ou maciço, onde se abriram propositadamente cavas, axialmente, para encaixar o
enrolamento indutor, tendo normalmente um grande comprimento e um pequeno diâmetro,
menor que um metro nas máquinas de grande potência. As cavas podem ser fechadas por talas
metálicas, em geral de bronze ou outro material não magnético. Assim o enrolamento indutor
resistirá muito bem à força centrífuga. Por conseguinte, a máquina de rotor cilíndrico pode
rodar a altas velocidades porque o seu rotor resiste bem aos esforços centrífugos a que fica
sujeito. Logo é susceptível de ser accionada por uma turbina a vapor que é uma máquina
motriz que trabalha a altas velocidades. Por este motivo a máquina de rotor cilíndrico é
também conhecida por turboalternador.
Fig. 1.2 – Vista em corte de um turbo alternador de 700MVA 50 Hz 3000r.p.m 20KV
Como se pode observar na figura 1.2 este tipo de rotor é feito de uma só peça cilíndrica
ao longo da qual são abertas cavas a receber os enrolamentos do campo indutor.
1.1.2 - Máquina Síncrona de Pólos Salientes
A máquina de pólos salientes deverá rodar a baixas velocidades, é em regra geral
accionada por turbinas hidráulicas que apresentam baixa velocidade, porque caso contrário
devido à configuração dos pólos a força centrifuga atingiria valores que poderiam
comprometer a resistência mecânica da fixação dos terminais polares.
Logo, o rotor de pólos salientes deverá ter um grande número de pólos para gerar f.e.m. à
frequência normalizada de 50 Hz. Tendo um grande número de pólos, tem em geral um
grande diâmetro e pequeno comprimento axial.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
3
A figura 1.3, permite ter uma ideia dos dois tipos de máquina, com a de pólos salientes
em cima e a de rotor cilíndrico em baixo. Os aspectos construtivos mais marcantes podem ser
aqui observados para máquinas com a mesma potência.
Núcleo do
estator
Terminais de
saída
Permutadores
de calor
Base
Enrolamentos
do estator
Veio
Excitador
Brushless
Pólos do
rotor
Ventoinha
Rolamento
de apoio
Excitador
Brushless
Enrolamentos
do estator
Núcleo do
estator
Fig. 1.3 - Comparação entre máquina de rotor de pólos salientes
e máquina de rotor cilíndrico.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
4
Nas figuras 1.4 e 1.5, podem ser comparados os dois tipos de rotores de máquinas
síncronas, em que na primeira está representado o rotor cilíndrico e na segunda o de pólos
salientes. Tendo o mesmo volume prismático D12 l1 = D22 l 2 , então as duas máquinas têm
potências equivalentes.
D1
l1
Fig. 1.4 - Gerador síncrono bipolar de rotor cilíndrico (turboalternador)
D1 < l1
l2
D2
Fig. 1.5 - Gerador síncrono hexapolar de rotor de pólos salientes (hidroalternador) D2 > l2
A frequência f da f.e.m. gerada no estator está relacionada com a velocidade do rotor
pela seguinte expressão,
f =
Np
60
(1.1)
onde N é o número de rotações por minuto e p o número de pares de pólos.
Os rotores cilíndricos como estão dimensionados para altas velocidades deverão ter um
pequeno número de pares de pólos, como foi salientado anteriormente. Por outro lado pode
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
5
ser observada na figura 1.6, a máquina síncrona de pólos salientes, também conhecida por
hidroalternador, onde a quantidade de pólos é sempre superior podendo ser cinco vezes mais.
Fig. 1.6 - Hidroalterador visto em corte
1 – Cobertura
2 - Anel colector
3 – Cruzeta superior
4 – Rotor de pólos Salientes
5 – Estator
6 – Pás de refrigeração
7 – Rolamento
8 – Cruzeta Inferior
9 – Eixo
10 – Aro de regulação
11 – Cobertura da turbina
12 – Pá directriz da turbina
13 - Travessa
14 – Conduta em expiral
15 – Turbina
16 – Conduta de Saída
17 – Tubo de sucção
Por ser normalmente accionada por uma turbina hidráulica a máquina com pólos salientes
é também conhecida por hidroalternador. Este tipo de hidroalternador é normalmente
instalado em grandes barragens como Castelo de Bode, Alqueva, etc. A figura 1.7 mostra
uma máquina deste tipo vista em corte. Este tipo de máquina possui também uma excitatriz
que é uma máquina de corrente continua que serve para excitar o circuito indutor do rotor
através de dois anéis exterior montados no veio do rotor e obviamente isolados. A corrente de
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
6
excitação é injectada através de duas escovas que assentam nos anéis do rotor. A excitatriz
está também directamente acoplada ao mesmo veio do gerador e da turbina. Posto isto, podese passar para a representação esquemática da máquina síncrona representada na figura 1.7.
A
Circuito de Carga
Estator
N
C
B
Excitatriz
Aneis
Pmec
Rotor
+
G
If
Escova
-
Fig. 1.7 - Esquema clássico de excitação da máquina síncrona de pólos salientes
A figura 1.7 representa o tipo clássico de excitação dos alternadores de forma
simplificada, os sistemas de excitação que são aplicados industrialmente, são evidentemente
mais complexos e sofisticados, pertencendo ao universo dos Sistemas de Controlo de um
centro produtor de energia. O controlo preciso sobre a corrente de excitação I f permite criar
um fluxo induzido no rotor, adaptativo às condições de carga, estes sistemas fazem parte de
controlo P.I.D.
Rotor
Estator
Fig. 1.8 – Pormenor de construção do estator e do rotor
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
7
O estator da máquina síncrona de pólos salientes consiste num núcleo laminado de
chapas de ferro macio empilhadas, com cavas internas, um grupo de enrolamentos trifásicos
distribuídos no estator e alojados nas cavas e uma protecção exterior que o envolve, onde
estão os rolamentos para o eixo do rotor.
O número de voltas dos enrolamentos do estator é igualmente distribuída sobre os pares
de pólos e os eixos das fases, desfasados 2π/3 radianos.
A sua construção está mais vocacionada para aplicações de baixa velocidade onde o rácio
do diâmetro com comprimento do rotor pode ser feito de forma a acomodar o maior número
de pólos. As máquinas síncronas de pólos salientes são frequentemente usadas nos
hidrogeradores para adaptarem a baixa velocidade de funcionamento dos hidrogeradores tal
como se pode observar na figura 1.6.
Na figura 1.9 pode-se observar um exemplo de uma secção em corte do rotor de pólos
salientes com enrolamento amortecedor. Os enrolamentos amortecedores são constituídos por
barras de cobre embutidas em cavas abertas nas peças polares e ligadas todas entre si por
meio de um anel. Resulta assim um enrolamento em gaiola ou em curto-circuito.
Enrolamento amortecedor
Enrolamento
de excitação
Enrolamento
amortecedor
Núcleo
Fig. 1.9 - Rotor de pólos salientes com enrolamento amortecedor
Na figura 1.10 pode observar-se um rotor de pólos salientes com as respectivas barras do
enrolamento amortecedor.
Fig. 1.10 - Perspectiva do rotor com 24 pólos salientes e dos enrolamentos amortecedores
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
8
1.2 - Princípio de Funcionamento da Máquina Síncrona
Por simplicidade vai ser considerada a máquina síncrona de rotor cilíndrico por ter um
entreferro constante, a distribuição da densidade de fluxo magnético ao longo da periferia do
rotor, ou do entreferro é sinusoidal. Este campo com o rotor parado é estacionário, semelhante
a um magneto permanente com um pólo norte e um pólo sul.
Quando o rotor for animado com movimento de rotação, o que se observa num
determinado ponto da periferia do estator, ou do entreferro, é um campo magnético de
intensidade variável entre dois máximos de sentidos opostos. Assim estão reunidas as
condições para a formação do campo girante. Este campo girante, vai induzir f.e.m.s nos
enrolamentos do estator. Em vazio as tensões aos terminais têm a forma indicada na figura
1.11.
Quando o rotor estiver parado em relação ao estator, não há variação de fluxo e portanto
não existe f.e.m. induzida, mesmo que o rotor esteja excitado.
Tensão
ua0 ( t )
ub0 ( t )
uc0 ( t )
240
3600
Umax
ωt
Uc
Ub
U aU
a
0
60
120
180
300
α = ωt
Ub
Uc
Diagrama vectorial
Diagrama temporal
Fig. 1.11 - Representação do sistema trifásico de tensões através do diagrama vectorial e temporal
1.2.1 - Equação Vectorial da Máquina Síncrona de Rotor Cilíndrico
Pretende-se estabelecer uma equação que relacione a tensão U aos terminais da máquina
em função da velocidade angular ω do rotor, da corrente de excitação I f e da corrente de
carga I debitada sobre um circuito de utilização Z u . Para isso vai ser considerado o esquema
de ligações simplificado representado na figura 1.12, em que o gerador alimenta uma carga
simétrica Z u . Aplicando a lei geral de indução ao caminho fechado γ no estator.
resulta,
d Ψ1
⎛ d Ψ1R d Ψ1E ⎞
E , d γ = i1r1 + U1 = −
= −⎜
+
t
dt
dt ⎟⎠
⎝ dt
v∫ (
)
J.L.F. – Máquina Síncrona em Regime Transitório
(1.2)
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
i1
A
Estator
9
γ
r1
L11
Zu
U1
Circuito de Carga
N
Zu
i2
C
B
i3
Zu
α
φr
ω
Rotor
+ if
Fig. 1.12 - Máquina síncrona simplificada
em que,
Ψ1 = Ψ1R + Ψ1E é o fluxo total ligado com a fase1 do estator.
Ψ1R é o fluxo ligado com a fase 1 produzido pelo rotor.
Ψ1E é o fluxo ligado com a fase 1 devido às três correntes do estator.
Quando a máquina está em vazio, as correntes das três fases são nulas, portanto a
d Ψ1R
representa a f.e.m. em vazio do gerador
expressão Ψ1E = 0 é nula. Logo, o termo −
dt
induzida na fase 1 devido à variação do fluxo produzido pelo movimento do rotor.
O fluxo ligado com a fase 1 produzido pelo rotor vale,
Ψ1R = I R + LR1
em que I R é a corrente do rotor e LR1 é o coeficiente de auto indução entre o rotor e a fase 1.
Como o rotor está animado de rotação com uma velocidade angular ω , LR1 não é
constante mas terá uma expressão do tipo,
LR1 = LR1max cos(α 0 + ωt )
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
10
em que α 0 é o ângulo que o eixo magnético do rotor e da fase 1 do estator formam entre si no
instante da origem dos tempos.
Ψ1R = I R + LR1max cos(α 0 + ωt )
(1.3)
Logo a f.e.m induzida no estator devido ao fluxo do rotor é dada por,
−
d Ψ1
= I R ωLR1max sen(α 0 + ωt ) = E0sen(α 0 + ωt )
dt
(1.4)
resultando uma tensão sinusoidal e de frequência igual à velocidade angular do rotor, da
seguinte forma,
e(t ) = E0 e j ωt e E0 = I R ωLR1max
(1.5)
donde se conclui que a amplitude da f.e.m. E0 é proporcional à corrente de excitação I f e à
velocidade angular ω do rotor. Para manter a frequência constante, o único processo capaz de
variar a f.e.m. da máquina em amplitude é através de variação da corrente de excitação.
Analisado o estator em carga têm-se que Ψ1E é o fluxo ligado com a fase 1 do estator
devido às correntes que percorrem o estator, ou seja
Ψ1E = i1L11 + i2 L21 + i3 L31
(1.6)
Em que L21 e L31 são os coeficientes de indução mútua entre a fase 1 e as fases 2 e 3
respectivamente.
Num sistema trifásico sem neutro existe a seguinte relação de correntes,
i1 + i2 + i3 = 0 donde
i3 = −i1 − i2
Substituindo em (1.6) resulta,
Ψ1E = i1L11 + i2 L21 + i3 L31 = i1 ( L11 − L31 ) + i2 ( L21 − L31 )
Simplificando,
Ψ1E = i1 ( L11 − L31 )
Considerando-se que o circuito magnético da máquina é simétrico e L21 = L31 , sendo L11
o coeficiente de indução relativo ao fluxo principal que liga a bobina 1 com a 2 e 3 e λ o
coeficiente de indução relativa ao fluxo de dispersão. Como os eixos magnéticos fazem um
ângulo de 120° entre si,
1
L31 = LM cos (120º ) = l11 cos (120º ) = − l11
2
(1.7)
A expressão de Ψ1E fica, então
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
11
⎛3
⎞
Ψ1E = i1 ⎜ l11 + λ ⎟ = i1L+
⎝2
⎠
3
Considerando-se L+ = l11 + λ , coeficiente de auto-indução trifásico, a f.e.m. induzida
2
na fase 1 então devido ao fluxo produzido pelas 3 correntes estatóricas é dado por,
−
d Ψ1E
di
= − L+ 1
dt
dt
(1.8)
Suprimindo por comodidade os índices 1 e substituindo as expressão (1.5) e (1.8) na
equação(1.1) resulta,
iR + U = E 0 e j ωt − L+
di
dt
ou,
U + L+
j ωt
di
+ iR = E0 e
dt
(1.9)
que é uma equação de valores instantâneos onde,
U - é a tensão simples (entre fase e neutro) aos terminais do estator.
di
- é uma queda de tensão indutiva devido às correntes que atravessam as três fases do
L+
dt
rotor.
iR - é a queda de tensão óhmica numa fase do estator.
Ee j ωt - é a f.e.m. induzida por fase em vazio devido ao rotor.
Em regime alternado sinusoidal e desprezando a saturação do circuito magnético tem-se,
U = Ue
j ωt
e I = Ie
j ωt
Substituindo na equação (1.9) resulta a seguinte equação vectorial,
E0 = U + r I + jωL+ I E0 = U + r I + jωL+ I
ou,
E0 = U + ( r + jX + ) I
⎛3
⎞
X + = ωL+ = ω ⎜ l11 + λ ⎟
⎝2
⎠
3
⎛
⎞
onde X + = ωL+ = ω ⎜ l11 + λ ⎟
⎝2
⎠
(1.10)
(1.11)
que se denomina por reactância síncrona.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
12
A equação (1.10) pode traduzir-se pelo esquema da figura 1.13, onde E0 = I R ωLR1max é
a amplitude da f.e.m. induzida no estator .
X+
ωL+
r
I
ω
ΨR
~
IR
E0
Ec
Zu
U
Fig. 1.13 – circuito equivalente da máquina síncrona
Quando a máquina está em carga, a f.e.m. existente na máquina não é E0 mas sim Ec
f.e.m. em carga o fluxo resultante na máquina não é Ψ R mas sim,
Ψ res = Ψ R + Ψ C
em que Ψ C = l+ I é o fluxo de reacção do estator sobre o rotor, logo da figura 1.13,
Ec = E0 − jωL+ I
(1.12)
ou ainda, pela tensão de saída,
U = E0 − ( r + jX + ) I
(1.13)
As equações deduzidas anteriormente permitem traçar o diagrama vectorial por fase,
devido a Behn Eschenbourgh, como está representado na figura 1.14 para uma carga Z u
indutiva.
j ω l+ I
E0
ΨC
ΨR
EC
Ψ res
jX + I
δ
j ωλ I
U
ϕ
rI
I
Fig. 1.14 – Diagrama vectorial da máquina síncrona de rotor cilíndrico
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
onde
13
ϕ - desfasagem
δ - ângulo de carga
X + - reactância síncrona
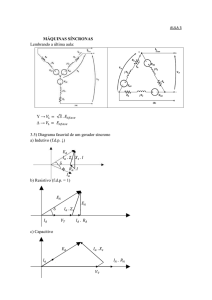
1.2.2 - Equação vectorial da Máquina Síncrona de Rotor de Pólos Salientes
Uma vez que a reactância do estator de uma máquina de pólos salientes varia com a
posição angular do rotor, Blondel resolveu o problema decompondo a reactância X ( β ) em
duas componentes X d segundo o eixo directo do rotor e X q segundo o eixo quadratura, de
acordo com a representação da figura 1.15. O mesmo acontece em relação à corrente I do
estator que se pode decompor em duas componentes I d e I q tal que I = I d + I q .
Com esta decomposição a equação vectorial de máquina escreve-se,
E 0 = U + rE I + jX d I d + jX q I q
(1.14)
cujo diagrama de Blondel está representado na figura 1.16. Em termos comparativos
pode-se observar o diagrama de Behn-Eschenbourg representado na figura 1.15 com o de
Blondel onde no cilíndrico X d = X q e o de pólos salientes onde X d > X q .
Como o fluxo do rotor φr tem a direcção do eixo directo, a f.e.m. E 0 , está desfasada
dele de 90º em atraso e portanto situada no eixo quadratura.
Desprezando a resistência rE do estator em face das reactâncias, o diagrama pode
simplificar-se eliminando os vectores rE I ,
rE I d e rE I q .
Iq
Id
Xd
I
Xq
Fig. 1.15 – Decomposição das correntes em eixo directo e
quadratura e reactâncias do eixo directo e quadratura
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
14
(
)
j Xd − Xq I d
(d)
φr
jX q I q
E0
δ
jX q I
rE I q
U
rE I d
ϕ
(q)
θ
jX d I d
rE I
I
Id
Iq
Fig. 1.16 – Diagrama de Blondel de rotor de pólos salientes
Assim a equação da máquina de pólos salientes em regime permanente, é
E 0 = U + rE I + jX d I d + jX q I − jX q I d
ou ainda ,
E 0 = U + rE I + jX d I d + j X d − X q I d
(
)
(1.15)
1.2.3 – Variação da Reactância em Função da Posição do Rotor
Numa máquina síncrona de pólos salientes como ilustra a figura 1.17 a reactância dos
enrolamentos varia com a posição angular β do rotor.
Eixo magnético
do enrolamento
β
Eixo directo
ou quadratura
Fig. 1.17 – Rotor de pólos salientes
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
15
A figura 1.18 a) mostra o fluxo segundo o eixo directo e a figura 1.18 b) o andamento do
fluxo segundo o eixo quadratura.
(d)
Permeância
Máxima
(q)
Permeância
Mínima
90º
(d)
(q)
Fig. 1.18 b) - Eixo quadratura ou transversal
Fig. 1.18 a) – Eixo directo ou
longitudinal
X q , com β = 90º
X d , com β = 0º
Como se pode observar destas figuras a permeância segundo o eixo directo é maior que a
permeância segundo o eixo quadratura. Então os coeficientes de auto-indução são,
Ld = n 2 Pd > Lq = n2 Pq
logo, X d > X q .
O andamento da reactância dos enrolamentos em função do ângulo β
durante uma
rotação completa do rotor está representado na figura 1.19, que apresenta dois ciclos de
rotação do rotor.
X (β)
Xd
Xq
0
90º
180º
270º
360º
β
Fig. 1.19 – Variação da reactância em função da posição do rotor numa máquina de pólos salientes
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
16
Define-se por coeficiente de saliência a seguinte relação,
α=
Xq
Xd
que vale α < 1 para um rotor de pólos salientes. O valor de α representa, o grau de saliência
do rotor, para α = 1 é o caso da máquina de rotor cilíndrico.
1.2.4 - Ensaio de Escorregamento para Determinação de Xd e Xq
No caso de uma máquina síncrona trifásica, ao aplicar um sistema trifásico de tensões ao
estator cria-se um campo girante que roda à velocidade síncrona. Para determinar X q bastava
pôr o rotor a rodar (com a excitação desligada) por meio de uma máquina de accionamento à
mesma velocidade angular ω do campo girante e em fase com ele, como indica a figura
1.20 a).
Medindo a corrente e a tensão, a reactância do eixo directo, viria (desprezando a
resistência).
Xd =
U
I min
Para determinar X q , bastava colocar o eixo directo do rotor em quadratura com o campo
girante, como indica a figura 1.20 b). Desprezando a resistência a reactância quadratura viria
U
Xq =
I max
ω
I min
ω
I max
ω
ω
U
ω
U
Campo girante
Fig. 1.20 a) – Medição de X d
J.L.F. – Máquina Síncrona em Regime Transitório
Fig. 1.20 b) – Medição de X q
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
17
Este ensaio é difícil, senão impossível de pôr em prática porque não se consegue colocar
o rotor rigorosamente em tais condições exactas. Na prática, para contornar esta dificuldade, é
usual fazer o chamado Ensaio de Escorregamento.
O ensaio de escorregamento consiste em aplicar ao estator, por intermédio de um
autotransformador, um sistema trifásico simétrico de tensões reduzidas (na ordem de 20 a
30% da tensão nominal a fim de proteger os enrolamentos da máquina) e com o rotor em
aberto colocá-lo a rodar com uma velocidade muito próxima da do campo girante do estator e
no mesmo sentido.
u
Saída da tensão
para o
Oscilocópio
i
Saída da imagem da
corrente para Osciloscópio
Estator
ωr = ωg ± ∆ω
Máquina de
accionamento
Rotor
er
Fig. 1.21 – Esquema de ligações do ensaio de escorregamento
O esquema de ligações para este ensaio está representado na figura 1.21.
Em seguida poder-se-ia medir a tensão aplicada e a corrente absorvida por meio de um
osciloscópio de dois canais, cujos picos são modulados pela permeância do rotor.
Eventualmente pode também oscilografar-se a f.e.m. induzida no rotor er devido à
diferença de velocidades ω − ωr do campo girante do estator e do rotor. O aspecto dos
referidos oscilogramas pode ser observado na figura 1.22.
Dos oscilogramas da tensão e da corrente vem,
U
X d = max
I min
J.L.F. – Máquina Síncrona em Regime Transitório
Xq =
U min
I max
2006
Capitulo 1 – Breve Descrição da Máquina Síncrona Trifásica
18
A ligeira flutuação na envolvente da tensão aplicada é devida à queda de tensão no autotransformador motivada pela flutuação da corrente.
Eixo
f.e.m.
induzida
er
Directo
Quadratura
Directo
π
0
Tensão
Simples u
Quadratura
2π
U min
U max
I min
I max
Xq
Xd
Corrente
na fase i
Fig. 1.22 – Oscilogramas típicos do ensaio de escorregamento
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capitulo 2 – Transformação de Park
Capítulo 2
19
Transformação de Park
2.1 - Transformação do Sistema Trifásico em Sistema Bifásico
O presente capítulo tem por objectivo explicar a conversão do sistema trifásico num
sistema bifásico, onde se irá basear todo o estudo de da máquina síncrona.
A transformação de Park é uma transformação de coordenadas que a partir dos três
enrolamentos a, b e c, desfasados de 120º e rodando com uma velocidade ω em relação ao
referencial (d, q) composto por dois enrolamentos pseudo-estacionários fazendo entre si um
ângulo de 90º como se pode observar na figura 2.1,
(q)
(c)
ic
uc
iq
ω
N
2
N
3
N
3
(a)
ia
uq
N
2
(p)
ω
ip
ua
ub
up
N
3
ib
(b)
Fig. 2.1 - Transformação de Park
Supondo que os três enrolamentos a, b e c, têm N/3 espiras por fase e os enrolamentos
peseudo-estacionários (d, q) têm N/2 espiras por fase, então temos as condições necessárias e
suficientes para relacionar os dois sistemas que permite considerá-los equivalentes.
De uma forma geral podemos assumir que as correntes i a , i b e i c constituem um sistema
trifásico assimétrico que pode ser decomposto em três sistemas, Directo, Inverso e
Homopolar.
A componente homopolar significa que as correntes dos três enrolamentos estão em fase,
sendo a sua equação,
i0 =
1
(ia + i b + ic)
3
Quando esta corrente percorre os três enrolamentos a, b e c, não produz nenhum campo
no entreferro da máquina, porque está em fase nos três enrolamentos.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
20
Capitulo 2 – Transformação de Park
A f.m.m. em cada um dos dois referenciais desta forma é dada por,
N
N
N
2π ⎞
N
4π ⎞
⎛
⎛
= i a cos (θ ) + i b cos ⎜ θ −
⎟ + i c cos ⎜ θ −
⎟
2
3
3
3 ⎠
3
3 ⎠
⎝
⎝
2π ⎞
4π ⎞
N
N
N
N
⎛
⎛
i q = i a sen (θ ) + i b sen ⎜ θ −
⎟ + i c sen ⎜ θ −
⎟
2
3
3
3 ⎠
3
3 ⎠
⎝
⎝
1
i 0 = (i a + i b + i c)
3
id
(2.1)
Simplificando a equação (2.1) obtém-se ainda,
2⎛
2π ⎞
4π ⎞ ⎞
⎛
⎛
i d = ⎜ i a cos (θ ) + i b cos ⎜ θ −
⎟ + i c cos ⎜ θ −
⎟
3⎝
3 ⎠
3 ⎠ ⎟⎠
⎝
⎝
2⎛
2π ⎞
4π ⎞ ⎞
⎛
⎛
i q = ⎜ i asen (θ ) + i bsen ⎜ θ −
⎟ + i csen ⎜ θ −
⎟
3⎝
3 ⎠
3 ⎠ ⎟⎠
⎝
⎝
i0 =
1
(i a + i b + i c )
3
que se pode escrever na seguinte forma matricial,
2π
4π ⎤
⎡id ⎤ 2 ⎡
⎢ id ⎥ = 3 ⎢ cos(θ ) cos(θ − 3 ) cos(θ − 3 ⎥
⎢ ⎥
⎢
⎥
⎢i ⎥
⎢sen(θ ) sen(θ − 2π ) sen(θ − 4π ) ⎥
⎢ q⎥
⎢
3
3 ⎥
⎢ ⎥
⎢
⎥
1
1
⎢i0 ⎥
⎢ 1
⎥
⎢⎣ ⎥⎦
⎢⎣ 2
⎥⎦
2
2
⎡ ia ⎤
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ib ⎥
⎢ ⎥
⎢i ⎥
⎢c⎥
⎣ ⎦
(2.2)
Considerando que se trata de um sistema trifásico equilibrado, a corrente homopolar é
nula e por conseguinte,
i0 =
1
(i a + i b + i c ) = 0
3
Assim, as equações relativas ao eixo directo e ao eixo quadratura podem-se representar
na seguinte forma,
2⎛
2π
⎛
i d = ⎜ i a cos (θ ) + i b cos ⎜ θ −
3⎝
3
⎝
4π
⎞
⎛
⎟ + i c cos ⎜ θ −
3
⎠
⎝
J.L.F. – Máquina Síncrona em Regime Transitório
⎞⎞
⎟⎟
⎠⎠
(2.3)
2006
21
Capitulo 2 – Transformação de Park
2⎛
2π
⎛
i q = ⎜ i asen (θ ) + i bsen ⎜ θ −
3⎝
3
⎝
4π ⎞ ⎞
⎞
⎛
⎟ + i csen ⎜ θ −
⎟
3 ⎠ ⎟⎠
⎠
⎝
(2.4)
Multiplicando (2.3) e (2.4) respectivamente por cos (θ ) e sen (θ ) , fica
2⎛
2π
⎛
i d cos (θ ) = ⎜ i a cos 2 (θ ) + i b cos (θ ) cos ⎜ θ −
3⎝
3
⎝
4π
⎞
⎛
⎟ + i c cos (θ ) cos ⎜ θ −
3
⎠
⎝
2⎛
2π
⎛
i qsen (θ ) = ⎜ i a sen 2 (θ ) + i bsen (θ ) sen ⎜ θ −
3⎝
3
⎝
4π ⎞ ⎞
⎞
⎛
⎟ + i csen (θ ) sen ⎜ θ −
⎟
3 ⎠ ⎟⎠
⎠
⎝
⎞⎞
⎟⎟
⎠⎠
(2.5)
(2.6)
Somado (2.5) com (2.6) resulta,
i a = i d cos(θ ) + i qsen(θ )
(2.7)
Esta relação só é válida quando a corrente homopolar é nula (caso do presente estudo)
O sistema trifásico pode ser representado, pelas três fases ia , ib e ic , forma,
i a = i d cos (θ ) + i q se n (θ ) + i c
2 ⎞
4 ⎞
⎛
⎛
i b = i d cos ⎜ θ − π ⎟ + i q se n ⎜ θ − π ⎟ + i c
3 ⎠
3 ⎠
⎝
⎝
2 ⎞
4 ⎞
⎛
⎛
i c = i d cos ⎜ θ − π ⎟ + i q se n ⎜ θ − π ⎟ + i c
3 ⎠
3 ⎠
⎝
⎝
(2.8)
Do mesmo modo pela forma matricial é possível representar o sistema de equações em
ordem às três fases a, b e c,
⎡ ia
⎢
⎢
⎢
⎢ib
⎢
⎢
⎢
⎢
⎢ic
⎣
⎤ = ⎡ cos(θ)
sen(θ)
1 ⎤ ⎡ id
⎥ ⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢ ⎛
2π ⎞
4π ⎞ ⎥ ⎢
⎛
θ
−
sen
⎥ ⎢ cos ⎜ θ −
⎟
⎜
⎟ 1 ⎥ ⎢iq
3 ⎠
3 ⎠ ⎥⋅⎢
⎝
⎥=⎢ ⎝
⎥ ⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢ cos ⎛ θ − 2π ⎞ sen ⎛ θ − 4π ⎞ 1⎥ ⎢
⎟
⎜
⎟ ⎥ ⎢ i0
⎥ ⎢ ⎜⎝
3
3
⎠
⎝
⎠ ⎦ ⎣
⎣
⎦
J.L.F. – Máquina Síncrona em Regime Transitório
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(2.9)
2006
22
Capitulo 2 – Transformação de Park
De forma semelhante para as equações das tensões,
⎡
⎢ ed
⎢
⎢
⎢ eq
⎢
⎢
⎢ e0
⎣
⎤ 2⎡
⎥ = ⎢ cos(θ )
⎥ 3⎢
⎥
⎢
⎥ = ⎢ sen(θ )
⎥
⎢
⎥
⎢ 1
⎥
⎢
⎣ 2
⎦
2π ⎞
4π ⎞ ⎤ ⎡
⎛
⎛
cos ⎜ θ − ⎟ cos ⎜ θ − ⎟ ⎥ ⎢ ed
3 ⎠
3 ⎠⎥ ⎢
⎝
⎝
2π ⎞
4π ⎞ ⎥ ⎢
⎛
⎛
sen ⎜ θ − ⎟ sen ⎜ θ − ⎟ ⎥ ⋅ ⎢ eq
3 ⎠
3 ⎠⎥ ⎢
⎝
⎝
⎥ ⎢
1
1
⎥ ⎢ e0
2
2
⎦ ⎣
⎡
⎢ ea
⎢
⎢
⎢ eb
⎢
⎢
⎢ ec
⎣
⎤ ⎡
⎤ ⎡
sen(θ)
1⎥ ⎢ ed
⎥ = ⎢ cos(θ)
⎥ ⎢
⎥ ⎢
⎥ ⎢ ⎛ 2π ⎞
⎛ 4π ⎞ ⎥ ⎢
⎥ = ⎢ cos ⎜ θ- ⎟ sen ⎜ θ- ⎟ 1⎥ ⋅ ⎢ eq
⎝ 3 ⎠ ⎥ ⎢
⎥ ⎢ ⎝ 3 ⎠
⎥ ⎢ ⎛ 2π ⎞
⎛ 4π ⎞ ⎥ ⎢
⎥ ⎢ cos ⎜ θ- ⎟ sen ⎜ θ- ⎟ 1⎥ ⎢ e0
⎝ 3 ⎠ ⎦ ⎣
⎦ ⎣ ⎝ 3 ⎠
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(2.10)
(2.17)
Esta conversão de eixos de trifásico em bifásico, é fundamental para o estudo da
máquina síncrona em regime transitório.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 3 – Equações Gerais da Máquina Síncrona
Capítulo 3
Equações Gerais da Máquina Síncrona
23
3.1 – Modelo da Máquina Síncrona de Pólos Salientes
Com base na transformação de Park apresentada no capítulo anterior, vão ser deduzidas
as equações da máquina síncrona de pólos salientes com enrolamentos amortecedores em
regime transitório.
A máquina síncrona generalizada é representada na figura 3.1.
(q)
KQ
ukq
ikq
M qkq
ω
Q
uq
iq
D
M df
F
id
M fkd
KD
if
ud
uf
(d)
ikd
ukd
Fig. 3.1. Máquina Síncrona de pólos salientes representada em dois eixos
Desta resulta que se podem extrair as figuras 3.2 e 3.3, que representam respectivamente
os circuitos equivalentes do eixo directo e eixo em quadratura. Estas representações
esquemáticas reflectem os modelos matemáticos da máquina síncrona, para o eixo directo e
em quadratura.
id
sla
f
ikd
sΨ d
id + ikd + if
iq
Uf v
if
rkd
Fig. 3.2 - Circuito equivalente do eixo directo
J.L.F. – Máquina Síncrona em Regime Transitório
ikq
rf
sLmd
sΨ q
slkd
sla
slf
ikq + iq
rkq
sLmq
slkq
Fig. 3.3- Circuito equivalente do eixo em quadratura
2006
Capítulo 3 – Equações Gerais da Máquina Síncrona
24
A partir dos esquemas equivalentes do eixo directo e quadratura respectivamente
representados pelas figuras (3.2) e (3.3), passa-se à construção do modelo matemático da
máquina.
Tendo em consideração as indutâncias dos enrolamentos podem-se decompor em,
Ld = Lmd + la
Lf = Lmd + lf
Lkd = Lmd + lkd
Lq = Lmq + lkq
(3.1)
Lkq = Lmq + lkq
A partir das enrolamentos da máquina síncrona pode escrever-se o seguinte sistema de
equações:
•
Para o eixo directo
uf = ⎡⎣ rf + ( L md +lf ) s ⎤⎦ if + Lmd s ikd + Lmd s id
ukd = 0 = L md s if + ⎡⎣ rkd + ( L md +lkd ) s ⎤⎦ ikd + Lmd s id
ψ d ( s ) = L md if + Lmd ikd + ( L md +la ) id
(3.2)
•
Para o eixo quadratura
(
)
ψ q ( s ) = L mq if + Lmq ikq + ( L mq +la ) iq
ukd = 0 = ⎡ rkq + L mq +lkq s ⎤ ikq + Lmd s iq
⎣
⎦
Resolvendo o sistema de equações do eixo Directo em ordem I d ( s ) , vem
id ( s ) =
rrf ++((LLmd ++ llf ))ss
L
s
Lmd
uuff ((ss))
f
md
f
md s
(L +
LLmd ss
rrkd +
+ lkd ))ss
00
md
kd + ( Lmd
md lkd
LLmd
L
Ψ d ((ss))
Lmd
Ψ
md
md
d
rf + ( Lmd + lf ) s
Lmd s
Lmd s
Lmd s
Lmd
rkd + ( Lmd + lkd ) s
Lmd
Lmd s
Lmd + la
=
A
B
(3.3)
O resultado do determinante A do numerador, vale
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 3 – Equações Gerais da Máquina Síncrona
25
A = Ψ d ( s ) r f rkd + Ψ d ( s ) r f L mds + Ψ d ( s ) r f lkd s + Ψ d ( s ) L mdrkd s + Ψ d ( s ) L mdlkd s 2 +
+Ψ d ( s ) l f rkd s + Ψ d ( s ) l f L mds 2 + Ψ d ( s ) l f lkd s 2 − vf ( s ) L mdrkd − vf ( s ) L mdrkd s
(3.4)
Factorizando, obtém-se a equação do determinante A (3.4) simplificada,
[(
)
]
A = Ψ d (s ) r f + (L md + l f )s (r kf + (L md + l kd )s ) − (L md )2 (s )2 +
[
]
(3.5)
+ v f (s )(L md )2 s − L md (r kd + (L md + l kd )s )
Voltando a factorizar por forma que a expressão fique do tipo τ= L/R ou seja em ordem à
constante de tempo do enrolamento, resulta
⎡ ⎛ L +l
L +l
A = rf rld ⎢1 + ⎜ md f + md kd
rf
rkd
⎢⎣ ⎝
⎛ l s⎞
+ Lmd rkd ⎜1 + kd ⎟ uf ( s )
rkd ⎠
⎝
⎞ ⎛ Lmd lkd + Lmd lf + lf lkd
⎟s +⎜
rf rkd
⎠ ⎝
⎞ 2⎤
⎟ s ⎥ ψd ( s ) +
⎠ ⎥⎦
(3.6)
Assim sob esta estrutura podem determinar-se algumas das seguintes constantes de tempo
fundamentais:
•
Constante de tempo transitória do enrolamento do eixo directo em circuito aberto,
L +l
1
( X md + X f )
T1 = T 'd0 = md f =
rf
ωrf
•
(3.7)
Constante de tempo transitória do enrolamento do eixo em quadratura em circuito
aberto,
L +l
1
( X md + X kd )
T2 = T 'q0 = md kd =
rkd
ωrkd
•
(3.8)
Constante de tempo subtransitória do enrolamento do eixo directo em circuito aberto,
' =
T3 = T 'd0
Lmd lf
1 ⎛
⎜⎜ l kd +
rkd ⎝
Lmd + Lf
⎞
1
⎟⎟ =
⎠ ωrkd
J.L.F. – Máquina Síncrona em Regime Transitório
⎛
X md X f
⎜⎜ X kd +
X md + X f
⎝
⎞
⎟⎟
⎠
(3.9)
2006
Capítulo 3 – Equações Gerais da Máquina Síncrona
•
26
Constante de tempo do enrolamento do eixo amortecedor eixo directo, em circuito
aberto,
l
X
Tkd = kd = kd
rkd ωrkd
(3.10)
Substituindo as constantes de tempo em (3.6), obtém-se,
⎤
⎡
A = rf rld ⎢ 1 + (T1 + T2 )s + T1T3s 2 ⎥ Ψd (s ) − Lmd rkd (1 + Tkd s )vf (s )
⎦⎥
⎣⎢
(3.11)
ou ainda,
A = rf rkd Lmd + rf rkd la + rf Lmd la s + rf lkd Lmd s + rf lkd la s + Lmd rkd la s + Lmd lkd la s 2 +
+ lf rkd Lmd s + lf rkd la s + lf Lmd la s 2 + lf lkd Lmd s 2 + lf lkd la s 2
Relativamente ao determinante B, vem
⎡
⎤
B = (Lmd + la )⎢[rf + (Lmd + l f )s ] [rkd + (Lmd + l kd )s ]⎥ − Lmd 2 s 2 −
⎣⎢
⎦⎥
[
]
[
− Lmd s Lmd rf + Lmd ( Lmd + lf ) s − Lmd 2 s + Lmd s Lmd 2 s − Lmd rkd − Lmd (Lmd + l kd )s
]
(3.12)
ou ainda,
⎡
⎡ ⎛ L +l
L +l ⎞
L l + Lmd lkd + lf lkd ⎤ 2 ⎤
B = rf rkd Ld ⎢ Lmd + la ⎢1 + ⎜ md kd + md f ⎟ s + md f
⎥s ⎥−
rkd
rf
rf rkd
⎢⎣ ⎝
⎥⎦ ⎥⎦
⎢⎣
⎠
⎡ L 2 L 2 ⎤ ⎡ L 2l
Lmd 2lkd ⎤ 2
md
md
md
f
−⎢
+
+
⎥s−⎢
⎥s
rf ⎥⎦ ⎢⎣ rf rkd
rf rkd ⎥⎦
⎢⎣ rkd
(3.13)
Simplificando (3.13) com a substituição de Ld = Lmd + la , obtém-se,
⎡ ⎛ 1 Lmd lf + Lmd la + lf la
1 Lmd lkd + Lmd la + lkd la
+
B = rf rkd Ld ⎢1 + ⎜
Lmd + la
rkd
Lmd + la
⎢⎣ ⎝ rf
L l + Lmd la + lf la Lmd lf la + Lmd lf lkd + Lmd la lkd + lf la lkd
+ rf rkd Ld md f
rf ( Lmd + la )
rkd ( Lmd lf + Lmd la + lf la )
J.L.F. – Máquina Síncrona em Regime Transitório
⎞ ⎤
⎟ s⎥ +
⎠ ⎥⎦
(3.14)
2006
Capítulo 3 – Equações Gerais da Máquina Síncrona
27
Como X=ω.L, as constantes de tempo resumem-se às seguintes expressões,
•
Constante de tempo transitória do enrolamento do eixo directo em curto circuito,
T4 = T 'd =
T5 =
•
1
rf
⎛ 1 Lmf lf + Lmd la + lf la
⎜⎜
Lmd + la
⎝ rf
1 Lmf l kd + Lmd la + l kd la
1
=
rkd
Lmd + la
rkd
⎞ 1 Lmd la
1
⎟⎟ =
=
⎠ rf Lmd + la ωrf
⎛
L l
⎜⎜ l kd md a
Lmd + la
⎝
⎞
1
⎟⎟ =
⎠ ωrkd
⎛
X md X a
⎜⎜ Xf +
X md + X a
⎝
⎞
⎟⎟
⎠
⎛
X md X a
⎜⎜ X kd +
X md + X a
⎝
(3.15)
⎞
⎟⎟
⎠
(3.16)
Constante de tempo subtransitória do enrolamento do eixo directo em curto circuito
T6 = T 'd' =
1
ωrkd
⎛ 1
X md X f X a
⎜⎜
+
⎝ ωrkd X md X f + X md X a + X f X a
⎞
⎟⎟
⎠
(3.17)
Logo, (3.14), escreve-se
B = rf rkd Ld ⎡⎣1 + (T4 + T5 ) s + T4T6 s 2 ⎤⎦
(3.18)
Portanto atendendo a (3.11) e (3.18), a equação (3.3) escreve-se
2⎤
⎡
A rf rld ⎣1 + (T1 + T2 ) s + T1T3 s ⎦ Ψ d ( s ) − Lmd rkd (1 + Tkd s ) uf ( s )
id = =
B
rf rkd Ld ⎡1 + (T4 + T5 ) s + T4 T6 s 2 ⎤
⎣
⎦
(3.19)
Resolvendo (3.19) em ordem a Ψd(s), fica
⎡1 + (T + T ) s + T T s 2 ⎤
⎡
⎤ L u (s)
1 + Tkd s
4
5
4 6
⎥ Ld id ( s ) + ⎢
⎥ md f
Ψd ( s ) = ⎢
2
2
rf
⎣⎢1 + (T1 + T2 ) s + T1T3 s ⎦⎥
⎣⎢ 1 + (T1 + T2 ) s + T1T3 s ⎦⎥
(3.20)
Após simplificação, (3.20) pode ainda escrever-se
Ψd ( s ) =
1
1
X d ( s )id ( s ) + G ( s )uf ( s )
ω
ω
(3.21)
onde,
X d ( s) =
1 + (T4 + T5 ) s + T4T6 s 2
1 + (T1 + T2 ) s + T1T3s 2
Xd
J.L.F. – Máquina Síncrona em Regime Transitório
(3.22)
2006
Capítulo 3 – Equações Gerais da Máquina Síncrona
G ( s) =
28
1 + Tkd s
X md
1 + (T1 + T2 ) s + T1T3 s rf
(3.23)
2
Resolvendo o sistema de equações do eixo Directo em ordem iq ( s) , vem,
iqq((ss)) =
rrkd + ( Lmq + lkq ) s
kd + ( Lmq + lkq ) s
00
LLmq
mq
Ψ q ((ss))
Ψ
q
rkd + ( Lmq + lkq ) s
Lmq s
=
(3.24)
C
D
Lmq + l
Lmq
a
onde o determinante do numerador,
[
)]
(
C = rkq + Lmq + l kq s Ψq ( s)
(3.25)
Por outro lado, o determinante do denominador,
D = rkq Lmq + rkqla + Lmqla s + lkq Lmq s + lkqla s
(3.26)
Factorizando (3.26), fica
D = rkq ( Lmq + la ) + ( Lmqla + Lmqlkq + lkq la ) s
(3.27)
de modo que a corrente do eixo em quadratura iq ( s) , escreve-se
iq ( s ) =
⎡ rkq + ( Lmq + lkq ) s ⎤ Ψ q ( s )
C
⎣
⎦
=
D rkq Lmq + la + ( Lmq la + Lmq lkq + lkq la ) s
(
)
(3.28)
donde,
(
)(
)
⎡r L +l + L l + L l +l l s ⎤
kq mq a
mq a mq kq kq a ⎦
Ψq (s)= ⎣
iq ( s )
⎡ rkq + Lmq lkq s ⎤
⎣
⎦
(
)
que ainda se pode escrever na forma
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 3 – Equações Gerais da Máquina Síncrona
⎛
Lmq la
⎜ lkq +
⎜
Lmq + la
⎝
1
1+
(lkq + Lmq ) s
rkq
1+
Ψ q ( s ) = Lq
1
rkq
29
⎞
⎟
⎟
⎠ i ( s)
q
(3.29)
Assim será,
•
T ''q =
Constante de tempo subtransitória do enrolamento do eixo quadratura em curto
circuito,
Lmqla
1 ⎛
⎜ lkq +
rkq ⎜⎝
Lmq + la
•
T ''q 0 =
⎞
X mq X a
1 ⎛
⎟=
⎜ X kq +
⎟ ωrkq ⎜
X mq + X a
⎠
⎝
⎞
⎟
⎟
⎠
(3.30)
Constante de tempo subtransitória do enrolamento do eixo quadratura em circuito
aberto,
(
)
(
1
1
lkq + Lmq =
X kq + X mq
rkq
ωrkq
)
Substituindo (3.30) e (3.31), em Ψ q ( s ) =
(3.31)
1 + T ''q
1 + T ''q 0
Lqiq ( s )
(3.32)
obtém-se,
Ψ q ( s) =
1
X q ( s )iq ( s )
ω
(3.33)
onde,
X q ( s) =
1 + T ''qs
1 + T ''q 0s
Xq
(3.33)
Foram assim calculadas as reactâncias directas e quadratura, bem como as constantes de
tempo transitórias e subtransitórias.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 4 – Constantes da Máquina Síncrona
Capítulo 4
Constantes da Máquina Síncrona
30
4.1 – Significado Físico dos Parâmetros da Máquina Síncrona.
Os parâmetros das máquinas que são fornecidos pelos construtores, são em regra geral as
reactâncias, resistências e constantes de tempo que normalmente derivam de medidas feitas ao
enrolamento do estator. O método mais comum para extrair os parâmetros necessários da
máquina, com um grau de confiança elevado é através dos oscilogramas de curto-circuito das
correntes do estator. Este obtém-se quando se aplica um curto-circuito simétrico ao estator
quando este está previamente em vazio e com a corrente de excitação e campo constante.
Em torno da envolvente de corrente contínua, uma porção do curto-circuito tipicamente é
representado por dois períodos de amortecimento distintos. Estes denominam-se por período
sub-transitório e transitório.
O período sub-transitório refere-se aos primeiros ciclos do curto-circuito, quando a
corrente se amortece muito rapidamente, atribuído essencialmente a variações de corrente nos
enrolamentos amortecedores. A taxa de amortecimento de corrente no período transitório é
mais lenta e é atribuída a variações das correntes dos enrolamentos de campo do rotor.
O teorema do fluxo constante é importante para determinar os valores iniciais dos fluxos
transitórios induzidos nos circuitos acoplados. A ligação de fluxos de qualquer circuito
indutivo com uma resistência finita e uma f.e.m. não pode variar instantaneamente. De facto,
se não houver resistência ou f.e.m. no circuito, esse fluxo de ligação permaneceria constante.
O teorema dos fluxos de ligação da constante pode assim ser usado para determinar as
correntes imediatamente depois de uma variação nos seus termos.
Através das figuras que se seguem, é possível observar as distribuições de fluxo numa
máquina síncrona durante o período sub-transitório, transitório e permanente, depois de uma
perturbação no estator.
Assim durante o período vigência destes regimes, o comportamento da máquina passa a
ser descrito em pormenor.
4.1.1 - Período Subtransitório
Significado físico das reactâncias subtransitórias X d'' e X q''
Neste período o enrolamento amortecedor provoca um escudo à penetração do fluxo do
estator. Então as reactâncias X d'' e X q'' do período subtransitório tornam-se mais pequenas do
que as reactâncias relativas ao caso do fluxo penetrar no rotor.
O comportamento do curto-circuito no estator com excitação if no rotor durante o
período transitório, é equivalente a fazer um curto-circuito no rotor quando se aplica uma
tensão externa no estator. Esta equivalência está representada esquematicamente na figura
(4.1).
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 4 – Constantes da Máquina Síncrona
31
i
U
if
U
c.c.
~
⇔
Real
Equivalente
c.c.
Curto circuito no rotor
Curto circuito no estator
Fig. 4.1 – Curto-circuito equivalente
O andamento do fluxo magnético no eixo directo (d) e em quadratura (q) pode ser
observado na figura (4.2).
Kd
Eixo Directo (d)
Kq
Eixo Quadratura (q)
Fig. 4.2 - Comportamento do caminho do fluxo durante o período subtransitório
K d representa o enrolamento do eixo directo e K q o enrolamento do eixo quadratura.
Estes enrolamentos aqui representados podem ser observados na figura (3.1).
Eixo Directo
Eixo Quadratura
X d'' < X d' < X d
X q'' < X q' ≈ X q
Desta relação conclui-se que X q'' > X d'' .
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 4 – Constantes da Máquina Síncrona
32
4.1.2 - Período Transitório
Significado físico das reactâncias transitórias X d' e X q'
À medida que as correntes dos enrolamentos amortecedores se dissipam durante o
período subtransitório, entra-se no período transitório onde as variações de corrente no
enrolamento de excitação reagem da mesma maneira que as correntes nos enrolamentos
amortecedores, mas mais lentamente.
Passado algum tempo após a criação desta barreira pelos enrolamentos amortecedores o
fluxo começa a penetrar no rotor, logo a reactância directa X d' e quadratura X q' começa a
aumentar. No entanto a penetração do fluxo magnético ao longo do ferro no eixo directo, é
maior do que a do eixo quadratura, logo
Eixo Directo (d)
X d' > X q
Eixo Quadratura (q)
Fig.4.2 - Comportamento do caminho do fluxo durante o período transitório
Eixo Directo
X d' < X d
Eixo Quadratura
X q ≈ X q'
4.1.3 – Regime Permanente
O regime permanente é alcançado, depois da sequência de perturbação inicial
subtransitória e transitória, o fluxo produzido pelo estator penetra em ambos os enrolamentos,
de campo e amortecedor do rotor.
A última obstrução à passagem do fluxo é a resistência de campo rf , este por fim acaba
por penetrar totalmente no rotor, chegando-se deste modo ao regime permanente.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 4 – Constantes da Máquina Síncrona
33
Neste caso X d > X q mas X q ≈ X q' .
Eixo Directo (d)
Eixo Quadratura (q)
Fig. 4.4 - Comportamento do caminho do fluxo em regime permanente
Xd > Xq
Analisado o comportamento físico da máquina síncrona quando sujeita ao curto circuito
nos seus três regimes temporais Subtransitório, Transitório e Nominal, passa-se para a
modelação em esquemas eléctricos equivalentes da máquina em vazio e em curto circuito.
A partir desta modelação é possível extrair as constantes de tempo da máquina e
reactâncias, a partir das quais se pode ter uma ideia do seu significado físico.
4.1.4 – Funcionamento do enrolamento amortecedor
Num rotor cilíndrico as oscilações são normalmente amortecidas devido ao atrito com o
ar e nas chumaceiras. Além disso sendo o rotor maciço em ferro forjado a rodar à velocidade
ω ± ∆ω induzem-se nele, durante as oscilações, correntes de Foucault de frequência ± ∆ω
que dão origem a perdas por efeito de Joule na massa do rotor que resultam da variação da
energia cinética. Por isso, o rotor tende a parar de oscilar, ficando a rodar à frequência
síncrona ω do campo girante.
Num rotor de pólos salientes, como é normalmente laminado, há necessidade de
incorporar um enrolamento fechado (enrolamento em curto circuito colocado nas faces
polares do rotor) chamado enrolamento amortecedor como pode ser observado na figura 1.10.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 4 – Constantes da Máquina Síncrona
34
O enrolamento amortecedor tem então as seguintes funções na máquina síncrona de pólos
salientes,
•
Amortecer as oscilações do rotor durante um pedido brusco de carga, de forma à
frequência do gerador síncrono variar apenas durante um curto espaço de tempo.
•
Eliminar as harmónicas produzidas pelo campo girante por reacção, de acordo com a
lei de Lenz. As harmónicas são devidas à existência de cavas e dentes no estator e à
descontinuidade da f.m.m. do enrolamento do estator.
•
Permitir o arranque da máquina síncrona como motor assíncrono. O enrolamento
amortecedor funciona como uma gaiola de esquilo. Quando o motor fica perto do
sincronismo, liga-se a corrente de excitação e o motor entra em sincronismo com a
rede ficando a rodar com uma velocidade constante como motor síncrono.
4.2 – Análise do modelo da máquina
O seguinte desenvolvimento, mostra como se determinam as constantes e equações
fundamentais da máquina, servindo para a simulação experimental das correntes de curto
circuito.
4.2.1 - Esquema Eléctrico do Regime Subtransitório
No regime subtransitório as correntes id , if , ikd e iq são diferentes de zero. Logo o
esquema equivalente da máquina síncrona para este regime representa-se pela figura (4.5),
Xa
rkd
rf
X kd
Xf
X md
X d''
Fig. 4.5 - Esquema do eixo directo em regime subtransitório circuito aberto
•
Reactância Subtransitória do eixo directo, em circuito aberto
Tendo por base o esquema equivalente do modelo da máquina síncrona passa-se a
determinar a equação da reactância subtransitória do eixo directo,
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 4 – Constantes da Máquina Síncrona
X ''d = X a +
35
X md X kd X f
1
= Xa +
1
1
1
X kd X f + X md X f + X md X kd
+
+
X md X kd X f
(4.1)
Do mesmo modo pode-se obter a constante de tempo subtransitória do eixo directo em
circuito aberto.
A reactância onde se baseia esta constante de tempo é a reactância vista do enrolamento
amortecedor directo,
⎛
⎞
⎜
⎟ 1 ⎛
L l ⎞
1
1
⎜ X kd +
⎟=
T 3 = T ''d 0 =
lkd + md f ⎟
⎜
1
1 ⎟ rkd ⎝
rkd ⎜
Lmd + lf ⎠
+
⎜
⎟
X
X
md
f ⎠
⎝
ou, simplificando,
T 3=T ''d 0 =
X md X f ⎞
1 ⎛
⎜ X kd +
⎟
ωrkd ⎝
X md + X f ⎠
(4.2)
Xa
rkq
X q''
X mq
X Kq
Fig. 4.6 - Esquema do eixo quadratura em regime subtransitório circuito aberto
Através da análise esquemática é possível determinar a,
•
Reactância subtransitória do eixo quadratura, em circuito aberto,
X ''q = X a +
•
1
1
1
+
X md X kq
Xa +
X mq X kq
X mq + X kq
(4.3)
Constante de tempo subtransitória do eixo quadratura, em circuito aberto,
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 4 – Constantes da Máquina Síncrona
36
L +l
1
''
T 2 = Tq0
X md + X kq
= md kd =
rkd
ωrkd
(
)
(4.4)
Xa
rkd
rf
X kd
Xf
X md
Fig. 4.7 - Esquema do eixo directo em regime subtransitório em curto-circuito
⎛
⎜
1
'' = 1 ⎜ X +
T 6 =T d
kd
1
1
1
ωrkd ⎜
+
+
⎜
X md X kd X f
⎝
⎞
⎟
⎟
⎟
⎟
⎠
Simplificando,
T 6 = T ''d =
⎞
X md X f X a
1 ⎛
⎜ X kd +
⎟
ωrkd ⎝
X md X f + X md X a + X f X a ⎠
(4.5)
Xa
rkq
X mq
X Kq
Fig. 4.8 - Esquema do eixo quadratura em regime subtransitório em curto-circuito
•
Constante de tempo subtransitória do eixo quadratura em curto-circuito,
⎛
⎞
⎜
⎟
⎛
X mq X a
1
'' = 1 ⎜ X +
⎟= 1 ⎜X +
Tq
a
kq
1
1 ⎟ ωrkd ⎜
X mq + X a
ωrkd ⎜
⎝
+
⎜
⎟
X
X
a
mq ⎠
⎝
J.L.F. – Máquina Síncrona em Regime Transitório
⎞
⎟
⎟
⎠
(4.6)
2006
Capítulo 4 – Constantes da Máquina Síncrona
37
4.2.2 - Esquema Eléctrico do Regime Transitório
No regime transitório o fluxo já penetrou no enrolamento amortecedor e está agora a
fazê-lo no enrolamento de campo. Aqui o enrolamento amortecedor já não contribui para o
regime transitório e portanto os esquemas reduzem-se à seguinte forma,
Xa
rf
X md
X d'
Xf
Fig. 4.9 - Esquema do eixo directo em regime transitório circuito aberto
•
Reactância transitória do enrolamento do eixo directo, em circuito aberto,
X 'd = X a +
•
X md X f
= Xa +
1
1
X md + X f
+
X md X f
1
(4.7)
Constante e tempo subtransitória do eixo directo em circuito aberto,
T 1 = T ''d 0 =
1
( X f + X md )
ωrf
(4.8)
A constante e tempo em curto-circuito fica,
Xa
rf
X md
Xf
Fig. 4.10 - Esquema do eixo directo em regime transitório curto-circuito
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 4 – Constantes da Máquina Síncrona
•
38
Constante de tempo subtransitória em curto-circuito,
⎛
1 ⎜
1
⎜ Xf +
T ''d =
1
1
ωrf ⎜
+
⎜
X a X md
⎝
⎞
⎟
X md X a ⎞
1 ⎛
⎟=
⎜ Xf +
⎟
X md + X a ⎠
⎟ ωrf ⎝
⎟
⎠
(4.9)
Xa
X q'
X mq
Fig. 4.11 - Esquema do eixo quadratura em regime transitório circuito aberto
•
Reactância transitória do eixo quadratura, em curto-circuito
X 'q = X a + X mq
•
(4.10)
Constante de tempo transitória do eixo quadratura em circuito aberto,
T 'q 0 = 0
Xa
X mq
Fig. 4.12 - Esquema do eixo quadratura em regime transitório curto-circuito
•
Constante de tempo transitória do eixo quadratura em curto-circuito,
T 'q = 0
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 4 – Constantes da Máquina Síncrona
39
4.2.3 - Esquema Eléctrico do Regime Permanente
Em regime permanente não há variação de fluxo através do enrolamento amortecedor
nem pelo enrolamento de campo, logo os esquemas da máquina síncrona reduzem-se da
seguinte forma,
Xa
Xd
X md
Fig. 4.13 - Esquema do eixo directo em regime permanente
•
Reactância síncrona do enrolamento do eixo directo, em circuito aberto
X d = X a + X md
(4.11)
Xa
Xq
X mq
Fig. 4.14 - Esquema do eixo quadratura em regime permanente
•
Reactância síncrona do enrolamento do eixo quadratura, em circuito aberto
X q = X 'q = X a + X mq
(4.12)
Este capitulo demonstrou pormenorizadamente o comportamento da máquina perante um
curto-circuito nos três regimes, subtransitório, transitório e permanente, realçando os
enrolamentos amortecedores e o seu comportamento durante a perturbação.
Para cada regime foram também desenvolvidas as equações das reactâncias e constantes
de tempo, recorrendo à representação esquemática da máquina.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5
Capítulo 5 – Equações do Curto-Circuito
Equações do Curto-Circuito
40
Neste capitulo vão ser desenvolvidas as equações das correntes de curto circuito para os
casos do curto-circuito trifásico simétrico, assimétrico fase-fase, assimétrico fase-neutro e
assimétrico fase-fase-neutro.
5.1 - Equações das Reactâncias
Tendo por base a simplificação da equação do fluxo magnético segundo o eixo directo
(3.20) obtida no Capitulo 3,
⎡1 + (T + T ) s + T T s 2 ⎤
⎡
⎤ L u (s)
1 + Tkd s
4
5
4 6
⎥ Ld id ( s ) + ⎢
⎥ md f
Ψd ( s ) = ⎢
rf
⎢⎣ 1 + (T1 + T2 ) s + T1T3 s 2 ⎥⎦
⎢⎣1 + (T1 + T2 ) s + T1T3 s 2 ⎥⎦
(3.20)
5.1.1 – Reactância Síncrona
Simplificando a equação (3.22) de 3ª ordem da reactância síncrona do eixo directo
obtém-se,
X d (s) = X d
1 + T 'ds + T 'dT ''ds 2
1 + T 'd0s + T 'd0T ''d0s 2
(5.1)
simplificando tendo por base o critério de que as constantes de tempo subtransitórias são
desprezáveis face às transitórias, com a intenção de baixar de ordem, considerou-se que
T 'd T ''d e T 'd 0 T 'd' 0
Eliminando na equação (5.1) as constantes de tempo desprezáveis, esta equação pode ser
escrita com uma grande aproximação, obtendo-se assim uma equação de 2ª ordem, mais fácil
de tratar.
X d ( s) = X d
(1 + T 'ds )(1 + T ''ds )
(1 + T 'd0s )(1 + T 'd0' s )
(5.2)
ou para conveniência de cálculo a reactância X d ( s ) pode ser transformada em admitância,
bastando para isso invertê-la,
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
(
)(
)(
41
'
''
1
1 1 + T d0s 1 + T d0s
=
X d ( s ) X d 1 + T 'ds 1 + T ''ds
(
)
)
(5.3)
expandindo a equação (5.3) em fracções parciais e criando por conveniência as variáveis A e
B vem,
1
1
A
B
=
+
'
X d ( s ) X d 1 + T ds
1 + T ''ds
(
) (
(5.4)
)
Calculando a variável A a partir de (5.4),
(
)(
)
'
''
Bs
1 1 + T d0s 1 + T d0s
1
1 + T 'ds + As +
1 + T 'ds
=
''
''
Xd
Xd
1 + T ds
1 + T ds
(
)
(
)
(
)
(
)
1
Substituindo o denominador de A da equação (5.5) por s = − '
Td
(5.5)
vem,
⎛ T 'd0 ⎞⎛ T ''d0 ⎞
B
−
⎜1 − ' ⎟⎜ 1 − ' ⎟
1 ⎝
1 ⎛ T 'd ⎞ A
T d ⎠⎝
Td ⎠
T 'd ⎛1 − T 'd ⎞
=
1− ' ⎟ − ' +
⎜
⎜
⎟
Xd
X d ⎝ T d ⎠ T d ⎛ T ''d ⎞ ⎝ T 'd ⎠
⎛ T d'' ⎞
⎜1 − ' ⎟
⎜1 − ' ⎟
⎝ Td ⎠
⎝ Td ⎠
simplificado mais,
⎛ T 'd0 ⎞⎛ T ''d0 ⎞
⎜ 1 − ' ⎟⎜ 1 − ' ⎟
1 ⎝
A
A
T d ⎠⎝
Td ⎠
=0− ' +0=− '
''
Xd
⎛ Td ⎞
Td
Td
⎜1 − ' ⎟
⎝ Td ⎠
(5.6)
Assumindo que as constantes de tempo subtransitórias são desprezáveis face às
transitórias então,
''
'
Ta'' Ta'
e Td0 Td
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
42
Tendo em conta esta simplificação e resolvendo (5.6) em ordem a “A” , obtém-se
⎛ 1 T 'd0 1 ⎞
−
A = Td' ⎜
⎟
'
⎝ Xd T d Xd ⎠
(5.7)
5.1.2 – Reactância Transitória
Tendo por base e a reactância transitória do eixo directo, deduzida no capítulo o anterior,
X d' = X a +
1
X md X f
= Xa +
1
1
X md + X f
+
X md X f
pode-se estabelecer também a seguinte equivalência,
'
X d' = X d T' d
T d0
(5.8)
por conseguinte substituindo a equação (5.8) na (5.7) obtém-se finalmente a equação da
variável A,
⎛ 1
1 ⎞
A = T 'd ⎜ ' −
⎟
⎜X
⎟
X
d
⎝ d
⎠
(5.9)
Calculando a variável B,
(
)(
)(
)
''
'
1 1 + T d0s 1 + Td0 s
1
As
1 + Td''s =
1 + Td''s
1 + Td''s + Bs
'
X d 1 + T ' s 1 + T ''s
Xd
1 + T ds
d
d
(
)
(
)
(
)(
)(
)
1
Substituindo o denominador de B por s = − '' vem,
Td
⎛ T 'd0 ⎞⎛ T ''d0 ⎞
⎜1 − '' ⎟⎜ 1 − '' ⎟
1 ⎝
B
T d ⎠⎝
Td ⎠
= 0 + 0 − ''
Xd
⎛ T 'd ⎞
Td
⎜ 1 − '' ⎟
⎝ Td ⎠
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
43
Assumindo novamente que as constantes de tempo subtransitórias são desprezáveis face
às transitórias T 'd0 T 'd' , T ''d0 > T ''d , T 'd T ''d a equação pode pode-se escrever,
'' ⎛ '
T 'd0T ''d0 ⎞
− B = T d ⎜ T d0
−
⎟
X d ⎝ T 'd
T 'dT ''d ⎠
Após simplificação a equação de variável B fica,
⎛ 1 T 'd0T ''d0 1 T ''d0 ⎞
B = T ''d ⎜
+
⎟
' ''
X
X d T 'd ⎠
T
T
⎝ d d d
(5.10)
5.1.3 – Reactância Subtransitória
Tendo por base a reactância subtransitória do eixo directo, deduzida no capítulo anterior,
X ''d = X a +
X md X kd X f
1
= Xa +
1
1
1
X kd X f + X md X f + X md X kd
+
+
X md X kd X f
(5.11)
Através da equação (5.11) pode-se estabelecer também a seguinte equivalência,
' ''
X d'' = X d T' dT ''d
T d0T d0
(5.12)
substituindo (5.12) em (5.11) obtém-se finalmente B,
⎛ 1
1 ⎞
B = T ''d ⎜ '' − ' ⎟
⎜X
⎟
⎝ d Xd ⎠
(5.13)
Revistando a equação da admitância (5.3) e substituindo as variáveis "A" representada na
equação (5.9) e B representada na equação (5.13), obtém-se a admitância operacional da
máquina síncrona para o eixo directo,
1
1 ⎛ 1
1
=
+⎜ ' −
X d ( s ) X d ⎝⎜ X d X d
⎞ T 'ds
⎛ 1
1 ⎞ Td''s
+
−
⎟
⎜
⎟
'
' ⎟
''
⎟
⎜ ''
⎠ 1 + T ds ⎝ X d X d ⎠ 1 + Td s
J.L.F. – Máquina Síncrona em Regime Transitório
(5.14)
2006
Capítulo 5 – Equações do Curto-Circuito
44
A admitância para o eixo em quadratura obtém-se directamente invertendo a equação
(3.34),
X q ( s) =
1 + T ''qs
1 + T ''q 0s
(3.34)
Xq
Simplificando (3.34) sob a forma de admitância, obtém-se,
(
(
)
)
1 + T ''q0s 1
1
=
X q (s)
1 + T ''qs X q
(5.15)
Finalmente e através de todo este desenvolvimento matemático foram alcançadas as
1
1
e
, que vão ser integradas nas equações das correntes de curtoadmitâncias
X q (s)
X d (s)
circuito.
5.2 - Equações Curto-Circuito Simétrico Trifásico em Vazio
A maior parte das falhas que ocorrem nos sistemas de distribuição de energia são não
simétricos entre fases. No entanto, a falha simétrica é importante porque, apesar ser rara é
mais grave porque desencadeia correntes mais elevadas de curto-circuito e provocaria
instabilidade no funcionamento da máquina, colocando-a em situações excepcionais de risco
para a sua integridade.
Além disso o curto-circuito simétrico é a condição mais simples de analisar e é o ponto
de partida para o estudo de qualquer tipo de falhas num sistema de potência. O ensaio de
curto-circuito simétrico de um gerador em vazio permite ainda calcular as características
transitórias da máquina, tais como constantes de tempo e reactâncias transitórias, que foram
desenvolvidas no item anterior.
ia
A
Estator
N
B
C
ic
ib
If
Rotor
Fig. 5.1 - Esquema do curto-circuito franco às três fases
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
45
5.2.1 - Equações das correntes nas Fases a, b e d
Considerando-se um alternador em vazio e que o brusco curto-circuito simétrico se dá no
instante inicial t=0, sendo λ o ângulo entre o eixo da fase “a” e o eixo directo no instante de
curto-circuito. Então, assumindo que a velocidade do alternador se mantém constante durante
todo o curto-circuito com a velocidade angular ω, o ângulo de fase é dado por, θ = ωt + λ .
Sabendo-se que a tensão instantânea da fase “a” em função das tensões do eixo directo e
tensão do eixo em quadratura é dada por,
ua = ud cos(θ) + uq sen(θ)
e substituindo θ = ωt + λ , vem,
ua = ud cos(ωt + λ) + uq sen(ωt + λ)
(5.16)
A partir da observação dos circuitos equivalentes do eixo directo e do eixo quadratura
representados respectivamente pelas figuras (3.2) e (3.3), podem-se extrair as equações (5.17)
e (5.18).
id
sla
ufvf
ikd
rf
rkd
id + ikd + if
sΨ d
if
sLmd
slf
slkd
Fig. 3.2 - Circuito equivalente do eixo directo
iq
sla
ikq
sΨ q
ikq + iq
rkq
sLmq
slkq
Fig. 3.3 - Circuito equivalente do eixo em quadratura
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
46
Por se tratar de curto-circuito simétrico a tensão do eixo quadratura e do eixo directo no
instante inicial U0=0 são dadas por,
ud =
d
Ψ d + ωΨ q + id ra = Ψ d s + ωΨ q + id ra
dt
(5.17)
uq = −ωΨ d +
d
Ψ q + iq ra = −ωΨ d + Ψ q s + iq ra
dt
Onde,
Ψ d = Lmdif + Lmdikd + ( Lmd + la ) id
(
(5.18)
)
Ψ q = Lmdikq + Lmq + la iq
Estando o alternador em vazio, quando surge um curto-circuito, as condições iniciais
antes do curto-circuito são as seguintes,
id = 0
ikd = 0
id0 = 0
ikd0 = 0
iq = 0
ikq = 0
ikq0 = 0
ikq0 = 0
ud0 = 0
uf = Constante
u
uq0 = −ωLmdif0 = − X md f = Emax0 = uq
rf
(valor de pico)
Desta forma o sistema trifásico de tensões iniciais aos terminais do alternador, antes do
curto-circuito pode ser observada na figura 1.12 respeitando o andamento temporal das
equações (5.19)
ua0 ( t ) = uq s e n(ωt + λ )
2π
)
3
4π
uc0 ( t ) = uq s e n(ωt − )
3
ub0 ( t ) = uq s e n(ωt −
(5.19)
Usando o princípio da sobreposição, desprezando a saturação do ferro, os valores finais
resultam assim da soma dos valores antes do curto-circuito, mais os valores das variações
durante o curto-circuito, estas condições estão representadas pelas equações (5.20).
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
47
ud = ud0 + ud'
uq = uq0 + uq'
id = id0 + id'
(5.20)
iq = iq0 + iq'
Substituindo as variáveis pelos respectivos valores iniciais, acham-se as equações que
definem as condições iniciais,
0 = 0 + ud' ⇒ ud' = 0
0 = uq0 + uq' ⇒ uq' = −uq0
id = 0 + id' ⇒ id' = id
iq = 0 + iq' ⇒ iq' = iq
uf = uf0 + uf' ⇒ uf' = 0
Aplicando as condições iniciais antes do curto-circuito na equação (5.17), obtém-se,
0 = Ψ 'd s + ωΨ 'q + id' ra
(5.21)
U q = −ωΨ d' + Ψ 'q s + iq' ra
por conseguinte as variações dos fluxos são:
•
antes do curto-circuito,
Ψd ( s ) =
1
1
X d ( s )id ( s ) + G ( s )uf ( s )
ω
ω
(5.22)
Ψq ( s ) =
•
1
X q ( s )iq ( s )
ω
depois do curto-circuito,
uf' = 0
1
1
1
X d ( s )id' ( s ) + G ( s )uf' = X d ( s )id' ( s )
ω
ω
ω
1
Ψ 'q ( s ) = X q ( s )i q' ( s )
ω
Ψ 'd ( s ) =
J.L.F. – Máquina Síncrona em Regime Transitório
(5.23)
2006
Capítulo 5 – Equações do Curto-Circuito
48
mantendo-se a tensão de excitação constante e substituindo (5.22) e (5.23) em (5.21),
0=
s
X d ( s)id' ( s) + X q ( s)iq' ( s ) + id' ra
ω
(5.24)
Uq
s
= −ωΨ 'd + Ψ 'q s + iq' ra = X d ( s )id' ( s) −
s
X q ( s )iq' ( s) − iq' ra
ω
ou ainda factorizando (5.24),
s
⎛
⎞
0 = ⎜ ra + X d ( s ) ⎟ id' ( s) + X q ( s)iq' ( s )
ω
⎝
⎠
(5.25)
s
⎛
⎞
= X d ( s )id' ( s ) − ⎜ ra + X q ( s ) ⎟ iq' ( s )
s
ω
⎝
⎠
Uq
Resolvendo o sistema de equações (5.25) em ordem a id' ( s ) e iq ( s ) obtém - se,
⎡
⎤ X ( s)
⎛ 1
ω2 ra 2
1 ⎞
2
2
= ⎢ s + ω + sωra ⎜
+
⎥ d 2 id' ( s )
⎟+
⎜
⎟
s
⎢⎣
⎝ X d ( s ) X q ( s) ⎠ X d ( s) X q ( s ) ⎥⎦ ω
Uq
(5.26)
⎡
⎤ X q (s)
⎛ 1
ω2ra 2
1 ⎞
iq' ( s )
= − ⎢ s 2 + ω2 + sωra ⎜
+
+
⎥
⎟
2
2
⎜
⎟
s
⎢⎣
⎝ X d ( s ) X q ( s ) ⎠ X d ( s ) X q ( s ) ⎥⎦ sω + ω ra
X d (s)
Uq
Tendo em consideração que a resistência da armadura é ra << Xd, podem-se desprezar os
termos ra 2 .
Também por aproximação reduzem-se X d ( s ) e X q ( s) às reactâncias
subtransitórias X d'' e X q'' , ficando por aproximação,
⎡
⎤
⎛ 1
1 ⎞ X ''
= ⎢ s 2 + ω2 + sωra ⎜ '' + '' ⎟ ⎥ 2d id' ( s )
⎜
⎟⎥
s
⎢
⎝ X d X q ⎠⎦ ω
⎣
Uq
(5.27)
⎡
⎤ ''
⎛ 1
1 ⎞ Xq '
= − ⎢ s 2 + ω2 + sωra ⎜ '' + '' ⎟ ⎥
i ( s)
⎜ X d X q ⎟ ⎥ sω q
s
⎢
⎝
⎠⎦
⎣
Uq
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
49
Fazendo com que a constante de tempo da armadura seja,
Ta =
1 ωra ⎛⎜ 1
1
=
+
α
2 ⎜ X d'' X q''
⎝
⎞
⎟
⎟
⎠
por conseguinte (5.27) pode escrever-se sob a forma de equação de transferência de segunda
ordem,
Uq
s
(
= s 2 + 2αs + ω2
X d'' '
id ( s )
ω2
)
(5.28)
Uq
s
(
2
2
= − s + 2αs + ω
X q'' '
iq ( s )
sω
)
ou ainda, resolvendo em ordem a id ( s ) e iq ( s ) ,vem
id ( s ) = id' ( s ) =
(
ω2
Uq 1
''
s 2 + 2αs + ω2 X d s
)
(5.29)
iq ( s ) = iq' ( s ) =
sω
Uq 1
''
- s 2 + 2αs + ω2 X q s
(
)
Substituindo (5.14) e (5.15) que representam respectivamente as admitâncias do eixo
directo e do eixo quadratura em (5.29),
⎛ 1
1
1 ⎛ 1
1 ⎞ Td' s
1 ⎞ Td''s
=
=
+
−
+
−
⎜
⎟
⎜
⎟
X d'' X d ( s) X d'' ⎜⎝ X d' X d ⎟⎠ 1 + Td' s ⎜⎝ X d'' X d' ⎠⎟ 1 + Td''s
1
(
(
)
)
''
s 1
1 + Tq0
1
=
=
''
X q'' X q ( s )
1 + Tq''s X q
1
(5.14)
(5.15)
obtém-se as equações de transferencia finais de id ( s ) e iq ( s ) .
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
id ( s) =
(
50
⎡ Uq ⎛ Uq Uq ⎞ T ' s
⎛ U q U q ⎞ T ''s ⎤
d
⎢
+⎜ ' −
+
⎟
⎜ '' − ' ⎟ d '' ⎥
'
2
2
⎜
⎟
s + 2αs + ω ( s + β ) ⎢⎣ X d ⎝ X d X d ⎠ 1 + Td s ⎜⎝ X d X d ⎟⎠ 1 + Td s ⎥⎦
ω2
)
(
(
)
)
⎡ 1 + T '' s
⎤
q0 U q ⎥
⎢
iq ( s) = 2
s + 2αs + ω2 ⎢ 1 + Tq''s X q'' ⎥
⎢⎣
⎥⎦
− sω
(5.30)
(5.31)
Fazendo a transformada inversa de Laplace de (4.30) e (4.31) obtém-se,
t
t
⎡
⎤
t
−
−
⎢ U q ⎛ U q U q ⎞ Td' ⎛ U q U q ⎞ Td'' U q − Ta
⎥
+⎜ ' −
+ ⎜ '' − ' ⎟ e
− '' e
cos ( ωt ) ⎥
id (t ) = ⎢
⎟e
⎜
⎟
⎜X
⎟
Xq
⎢ Xd ⎝ Xd Xd ⎠
⎥
⎝ d Xd ⎠
⎣
⎦
(5.32)
t
Uq −T
iq (t ) = − '' e a s e n ( ωt )
Xq
(5.33)
Sabendo que a corrente em cada fase é dada por (3.14),
i a = i d cos ( θ ) + i q s e n ( θ ) + i c
2 ⎞
4 ⎞
⎛
⎛
i b = i d cos ⎜ θ − π ⎟ + i q s e n ⎜ θ − π ⎟ + i c
3 ⎠
3 ⎠
⎝
⎝
(3.14)
2 ⎞
4 ⎞
⎛
⎛
i c = i d cos ⎜ θ − π ⎟ + i q s e n ⎜ θ − π ⎟ + i c
3 ⎠
3 ⎠
⎝
⎝
A corrente ia (t ) fica,
⎡
⎢ Uq ⎛ Uq Uq
ia (t ) = ⎢
+⎜ ' −
⎜
⎢ Xd ⎝ Xd Xd
⎣
t
t
−
− ⎤
⎞ T ' ⎛ U q U q ⎞ T '' ⎥
⎟ e d + ⎜ '' − ' ⎟ e d ⎥ cos ( ωt + λ ) −
⎟
⎜X
⎟
⎥
⎠
⎝ d Xd ⎠
⎦
(5.34)
t
t
Uq −T
Uq −T
− '' e a cos ( ωt ) cos ( ωt + λ ) − '' e a sen ( ωt ) sen ( ωt + λ )
Xq
Xq
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
51
A segunda parcela de (5.34),
−
Uqe
t
Ta
⎡ 1
⎤
1
⎢ − '' sen 2 ( ωt ) cos ( λ ) − '' cos ( ωt ) sen ( ωt ) sen ( λ ) ⎥
Xd
⎣⎢ X d
⎦⎥
pode simplificar-se recorrendo às seguintes relações trigonométricas,
cos 2 ( ωt ) = 1 − sen 2 ( ωt )
sen 2 ( ωt ) = 1 − cos 2 ( ωt )
1
cos ( ωt ) sen ( ωt ) = sen ( 2ωt )
2
e escreve-se,
t
t
U q − T X d'' + X q''
U q − T X d'' + X q''
a
cos ( λ ) −
cos ( 2ωt + λ )
−
e
e a
'' ''
2
2
Xd Xq
X d'' X q''
(5.35)
donde se podem retirar as constantes Xm e Xn,
Xm =
(
2 X d'' + X q''
)
X d'' + X q''
Xn =
(
2 X d'' + X q''
)
X d'' − X q''
(5.36)
Logo as equações de curto-circuito para as outras duas fases, ib (t ) e ic (t ) , escrevem-se:
•
para a fase B
t
t ⎤
⎡
−
−
⎢ Vq ⎛ Vq Vq ⎞ T ' ⎛ Vq Vq ⎞ T '' ⎥
2π ⎞
⎛
ib (t ) = ⎢
+⎜
−
−
⎟e d + ⎜
⎟ e d ⎥ cos ⎜ ωt + λ −
⎟−
⎜ X ' Xd ⎟
⎜ X '' X ' ⎟
X
3
⎝
⎠
d
⎢
⎥
d⎠
⎝ d
⎠
⎝ d
⎣
⎦
t
t
⎛
⎞
−
−
V
V
2
2π ⎞ ⎟
π
q
⎛
⎞
⎛
⎜ q
Ta
Ta
cos ⎜ λ − ⎟ +
cos ⎜ 2ωt + λ − ⎟ ⎟
e
e
−⎜
3
3 ⎠⎟
X
X
⎝
⎠
⎝
m
n
⎜
⎝
⎠
J.L.F. – Máquina Síncrona em Regime Transitório
(5.37)
2006
Capítulo 5 – Equações do Curto-Circuito
•
52
para a fase C
t
t ⎤
⎡
−
−
⎢ Vq ⎛ Vq Vq ⎞ T ' ⎛ Vq Vq ⎞ T '' ⎥
4π ⎞
⎛
ic (t ) = ⎢
+⎜
−
−
⎟e d + ⎜
⎟ e d ⎥ cos ⎜ ωt + λ −
⎟−
⎜ X ' Xd ⎟
⎜ X '' X ' ⎟
X
3
⎝
⎠
d
⎢
⎥
d⎠
⎝ d
⎠
⎝ d
⎣
⎦
t
t
⎛
⎞
−
−
4π ⎞ Vq Ta
4π ⎞ ⎟
⎛
⎛
⎜ Vq
Ta
cos ⎜ λ − ⎟ +
cos ⎜ 2ωt + λ − ⎟ ⎟
e
e
−⎜
3
3 ⎠⎟
X
X
⎝
⎠
⎝
n
⎜ m
⎝
⎠
(5.38)
5.2.2 - Equação da Corrente de Campo
As equações da corrente de campo da máquina antes do curto-circuito ou seja em regime
permanente, são da seguinte forma,
uf = rf if
ud = ra id + X qiq
(5.39)
uq = − X mdif + X did + ra iq
Antes do curto-circuito, o gerador considera-se em vazio e por conseguinte,
id = iq = 0 logo,
if0 = −
U q0
X md
=−
Uq
X md
A corrente de campo if , obtém-se impondo à corrente if0 antes do curto-circuito a
corrente if' , representando-se da seguinte forma,
if = if0 + if'
(5.40)
Durante o curto-circuito relação entre if' e id' pode obter-se a partir do seguinte sistema
de equações,
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
53
'
U f' = 0 = ⎡⎣ rf + ( Lmd + lf ) s ⎤⎦ if' ( s ) + Lmdikd
( s ) s + Lmdid' ( s ) s
(5.41)
(
)
'
'
U kd
= 0 = Lmdif' ( s ) s + ⎡ rkd + Lmd + l kd s ⎤ ikd
( s ) + Lmdid' ( s ) s
⎣
⎦
'
Visando a simplificação do sistema anterior, inicia-se o processo eliminando ikd
( s ) , entre
as duas equações vem,
(
)
(
)
⎡ ⎡r + ( L + l ) s ⎤ ⎡r + L + l
s ⎤ − Lmd 2 s 2 ⎤ if' ( s ) + Lmd s rkd + l kd s id' ( s ) = 0 (5.42)
md
f ⎦ ⎣ kd
md
kd ⎦
⎣⎢ ⎣ f
⎦⎥
Substituindo em (3.42) o valor de id' ( s ) já calculado anteriormente, obtém-se,
id' ( s ) =
(
ω2
1 Uq
s 2 + 2αs + ω2 X d ( s ) s
)
simplificando,
id' ( s ) =
Uq 1
(1 + Td0' s )(1 + Td0'' s ) ω2
(1 + Td' s )(1 + Td''s ) ( s2 + 2αs + ω2 ) X d (s) s
(5.43)
a corrente de campo vem,
if' ( s ) =
Lmd s (1 + Tkd s )
(
'
rf 1 + Td0
s
i' ( s )
'' d
1 + Td s
)(
)
simplificando,
if' ( s ) =
(
(1 + Tkd s )
)(
'
s 1 + Td'' s
1 + Td0
)(
ω2
X md Vq 1
s 2 + 2αs + ω2 X d rf s
)
(5.44)
Expandindo a equação (5.44) em fracções parciais, a transformada inversa de Laplace
vem,
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
54
t
⎡ −t
⎤
t
−
−
⎛
⎞
'
U
X
⎥
Tkd
q md ⎢ Td
Td'' Tkd
Ta
'
if (t ) = −
cos ( ωt ) ⎥
− ⎜1 − '' ⎟ e
− '' e
⎢e
'
⎜
Td ⎟⎠
Td
ωTd rf X d ⎢
⎥
⎝
⎣
⎦
(5.45)
Simplificando a primeira metade de (5.45),
−
U q X md
ωTd' rf X d
=
if0 X md 2
ωTd' rf X d
= if0
'
− Td'
Td0
Td'
= if0
X d − X d'
X d'
visto que,
'
Td0
− Td' =
1
ωrf
X X ⎞
1
1 ⎛
( X f + X md ) − ⎜ X f − md a ⎟ =
ωrf
ωrf ⎝
X md + X a ⎠
⎛
X md X a
⎜ X f + X md − X f −
X md + X a
⎝
⎞ X md ⎛
Xa ⎞
⎟=
⎜1 −
⎟
Xd ⎠
⎠ ωrf ⎝
X md
X md 2
( Xd − Xa ) =
ωrf X d
ωrf X d
Consequentemente a corrente de campo total depois do curto-circuito, é, if = if0 + if'
⎛ X − X'
d
if (t ) = if0 + if0 ⎜ d
⎜ X'
d
⎝
⎡ − t
⎞⎢ T' ⎛ T
⎟ ⎢e d − ⎜1 − kd
⎟
⎜
Td''
⎠⎢
⎝
⎣
t
⎤
t
−
−
⎞ T '' T
⎥
T
⎟ e d − kd e a cos ( ωt ) ⎥
''
⎟
Td
⎥
⎠
⎦
(5.46)
5.2.3 - Equação do Binário Resistente
O binário resistente oferecido pelo gerador durante o curto-circuito é dado por ,
(
)
T = ⎡⎣ Lmd if + Lmd ikd + ( Lmd + la ) id ⎤⎦ iq − ⎡ Lmq ikq + Lmq + la iq ⎤ id
⎣
⎦
(5.47)
Simplificando (5.47) obtém-se,
T = Ψ d iq − Ψ q id
Sendo este binário resistente por unidade de velocidade (1 rad/s). Para a velocidade ω,
obtém-se,
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
(
T = ω Ψ d iq − Ψ q id
55
)
Onde o fluxo por eixo é dado por,
Ψ d = Lmd if + Lmd ikd + ( Lmd + la ) id
Ψ q = Lmq ikq + ( Lmd + la ) iq
Antes do curto-circuito, existem as seguintes condições iniciais,
id0 = iq0 = 0
logo,
if0 = −
Uq
X md
Ψ d0 = Lmdif0 = −
Uq
ω
Ψ q0 = 0
Depois do curto-circuito, os valores dos fluxos são,
Ψ d = Ψ d0 + Ψ 'd = −
Uq
ω
+ Ψ 'd
Ψ q = Ψ q0 + Ψ 'q = Ψ 'q
Como já foi visto anteriormente, a equação de transferência de segunda ordem, é
Ψ 'd ( s ) =
X d (s) '
1
ω
id ( s ) =
Uq
s
ω
s 2 + 2αs + ω2
(
)
Aplicando a transformada inversa de Laplace obtém-se,
t
⎡
⎤
−
U
q⎢
Ta
'
Ψ d (t ) =
1− e
cos ( ωt ) ⎥⎥
⎢
ω
⎢⎣
⎥⎦
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
56
Simplificando,
t
Uq −T
Ψ d (t ) = −
e a cos ( ωt )
ω
(5.48)
Da mesma forma para o eixo quadratura obtém-se,
Ψ 'q ( s ) =
X q (s) '
ω
iq ( s ) =
Uq
2
2
ω
s + 2αs + ω
(
)
Aplicando a transformada inversa de Laplace obtém-se,
Uq
Ψ 'q (t ) = −
ω
−
e
t
Ta
sen ( ωt )
Simplificando,
t
Uq −T
Ψ q (t ) = −
e a sen ( ωt )
ω
(5.49)
A combinação dos fluxos Ψd e Ψq , que variam sinusoidalmente, dão origem a um fluxo
girante de velocidade ω que é estacionário em relação à armadura. Mas a sua amplitude
amortece-se com a constante de tempo ta .
Atendendo às equações (5.32) e (5.33) desenvolvidas anteriormente e substituído-as em,
(
T = ω Ψ d iq − Ψ q id
)
Obtém-se a equação final do binário,
T (t ) = U q 2e
−
t
Ta
t
⎡
−
⎛
⎞
⎛ 1
⎢ 1
1
1
1
T'
sen ( ωt ) ⎢ ' + ⎜ ' −
⎟ e d + ⎜ '' − '
⎜
⎟
⎜X
⎢ Xd ⎝ Xd Xd ⎠
⎝ d Xd
⎣
t ⎤
−
⎞ T'' ⎥
⎟e d ⎥ +
⎟
⎥
⎠
⎦
(5.50)
t
⎛ 1
Uq2 −T
1 ⎞
e a sen ( 2ωt ) ⎜ '' − '' ⎟
+
⎜ Xd Xq ⎟
4
⎝
⎠
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
57
5.3 - Curto-Circuito Trifásico Assimétrico Fase-Fase em Vazio
ia = 0
A
ic = −ib
Estator
N
B
C
ic
ib
If
Rotor
Fig. 5.2 - Esquema do curto circuito assimétrico Fase-Fase
5.3.1 - Equações das Correntes nas Fases
Este tipo de curto-circuito tem muitas semelhanças com o Fase-Neutro, o que os
diferencia é que o curto-circuito Fase-Neutro envolve também as impedâncias de sequência
de fase zero da máquina e qualquer impedância ligada entre o neutro e a terra, se o curtocircuito se der entre a fase e a terra.
Para o curto-circuito entre as fases “B” e “C” têm-se as seguintes condições,
eb − ec = 0
ib + ic = 0
(5.51)
ia = 0
Se a resistência da armadura for desprezada e os fluxos de ligação das fases a e b forem
mantidos constantes nos seus valores iniciais tem-se,
Ψ b − Ψ c = Ψ b0 − Ψ c0
(5.52)
Se o ângulo da máquina no qual ocorre o curto-circuito for λ então,
Ψ b0 = Ψ d0 cos(λ − 120°) − Ψ q0 sen(λ − 120°)
Ψ c0 = Ψ d0 cos(λ − 120°) − Ψ q0 sen(λ − 120°)
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
58
ou,
Ψ b0 − Ψ c0 = 3(Ψ d0sen(λ ) + Ψ q0 cos(λ ))
(5.53)
Usando as equações de transformação das correntes obtidas na matriz (2.15) e tensões
obtidas em (2.17), são obtidas as seguintes relações,
ed sen(ωt + λ ) + eq cos(ωt + λ ) = 0
id cos(ωt + λ ) + iq sen(ωt + λ ) = 0
(5.54)
i0 = 0
As equações obtidas em (5.54) juntamente com simplificações já desenvolvidas para o
curto-circuito trifásico simétrico, deram origem à seguinte equação para o curto-circuito
trifásico assimétrico para a fase B,
t
⎡
−
'
⎢
⎛
⎞ T
d( f-f )
1
1
1
⎢
⎜
⎟
ib
e
+⎜
−
+
(t ) = 3U q ⎢
⎟
( f-f )
+
X d + X 2 ⎜ X d'
X
X
+
X
d
2
⎟
2
⎢
⎝ ( f-f )
⎠
⎢
⎣
⎛
⎞
1
1
⎜
⎟
+⎜
−
⎟e
''
'
+
+
X
X
X
X
⎜ d( f-f )
2
d( f-f )
2⎟
⎝
⎠
∞
× ∑ ( −b ) sen ( (2n − 1) ( ωt ) ) +
n
n=0
J.L.F. – Máquina Síncrona em Regime Transitório
−
t
''
T
d( f-f )
(5.55)
×
3U q sen(λ ) ⎛ 1 ∞
⎞
n
⎜ + ∑ ( −b ) cos(2nωt ) ⎟ e
X2
⎝ 2 n =1
⎠
−
t
Ta
( f-f )
2006
Capítulo 5 – Equações do Curto-Circuito
59
para a fase C,
t
⎡
−
'
⎢
⎛
⎞ T
d f-f
1
1
1
⎢
⎜
⎟
ic
e ( ) +
+⎜
−
(t ) = − 3U q ⎢
⎟
( f-f )
X + X 2 ⎜ X d'
+ X2 Xd + X2 ⎟
⎢ d
( f-f )
⎝
⎠
⎢
⎣
−
t
⎛
⎞ T ''
d( f-f )
1
1
⎜
⎟
+⎜
−
×
e
⎟
''
'
+
+
X
X
X
X
⎜ d( f-f )
2
d( f-f )
2⎟
⎝
⎠
∞
× ∑ ( −b ) sen ( (2n − 1)(ωt) ) +
n
n=0
(5.56)
3U q sen(λ ) ⎛ 1 ∞
⎞
n
⎜ + ∑ ( −b ) cos(2nωt) ⎟ e
X2
⎝ 2 n =1
⎠
−
t
Ta
( f-f )
5.3.2 – Equação da Corrente de Campo
Para a corrente de excitação,
⎛ X − X'
d( f-f )
⎜ d
(t ) = if0 + if0 ⎜
if
'
( f-f )
⎜ X d( f-f )
⎝
⎡ − t
⎞⎢ T'
⎛
T
⎟ ⎢ d( f-f ) ⎜
− ⎜ 1 − kd
⎟ ⎢e
''
⎟⎢
⎜ Td( f-f )
⎠
⎝
⎢⎣
⎤
t
−
⎞ − t
⎥
Ta
Tkd
⎟ Td''
f-f )
(
−
cos ( ωt ) ⎥
e
⎟e
''
⎥
Td
⎟
⎥
( f-f )
⎠
⎥⎦
(5.57)
As constantes das equações (5.56) e (5.57) são dadas por,
X 2 = X d''
X q''
f-f
( ) ( f-f )
Td''
( f-f )
Ta
''
= Td0
( f-f )
( f-f ) =
b=
X d''
( f-f )
+ X2
X d'
( f-f )
+ X2
X2
ra
J.L.F. – Máquina Síncrona em Regime Transitório
X q''
( f-f )
− X d''
( f-f )
X q''
( f-f )
+ X d''
( f-f )
Td'
( f-f )
'
= Td0
( f-f )
X d'
( f-f )
+ X2
Xd
( f-f )
+ X2
(5.58)
2006
Capítulo 5 – Equações do Curto-Circuito
60
5.4 - Curto-Circuito Trifásico Assimétrico Fase-Neutro em Vazio
ia
A
in
Estator
N
B
C
ic = 0
ib = 0
If
Rotor
Fig.5.3 – Esquema do curto circuito assimétrico Fase-Neutro
5.4.1 - Equações das Correntes na Fase e no Neutro
Para o curto-circuito Fase-Neutro as condições de fronteira são,
ea = 0
ib = ic = 0
Considerando a resistência da armadura zero,
Ψ a = Ψ a0
Tendo como base a análise do curto circuito fase-fase, o de fase-neutro partilha o mesmo
princípio teórico visto serem ambos curto-circuitos assimétricos.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
61
Assim a equação da corrente do curto-circuito fase neutro representa-se, entre a fase A e
o neutro,
t
⎡
−
⎞ T ''
⎢⎛
d f-n
1
1
⎜
⎟
−
(t ) = 3U q ⎢⎜
ia
e ( ) +
⎟
⎢ X ''
( f-n )
+ X 2 + X 0 X d'
+ X2 + X0 ⎟
⎢⎜⎝ d( f-n )
( f-n )
⎠
⎢⎣
⎛
1
1
⎜
+⎜
−
'
⎜ X d( f-n ) + X 2 + X 0 X d + X 2 + X 0
⎝
−
t
⎞ T'
⎤
d( f-n )
1
⎟
+
e
⎥×
⎟
X d + X 2 + X 0 ⎥⎦
⎟
⎠
(5.59)
t
∞
⎛
⎞ − Ta
λ
3
cos(
)
U
1
×
( −b0 )n cos ( (2n − 1) ( ωt ) ) − q 1 ⎜⎜ + ( −b0 )n cos(2nωt) ⎟⎟ e ( f-n )
⎟
X 2 + X 0 ⎜⎝ 2 n =1
n=0
⎠
2
∞
∑
∑
5.4.2 - Equação da Corrente de Campo
⎛ X − X'
d( f-n )
⎜ d
(t ) = if0 + if0 ⎜
if
'
( f-n )
⎜ X d( f-n )
⎝
⎡ − t
⎞⎢ T'
⎛
T
⎟ ⎢ d( f-n ) ⎜
− ⎜ 1 − kd
⎟ ⎢e
''
⎟⎢
⎜ Td( f-n )
⎠
⎝
⎢⎣
⎤
t
−
⎞ − t
⎥
Ta
Tkd
⎟ Td''
f-n )
(
−
cos ( ωt ) ⎥
e
⎟e
''
⎥
Td
⎟
⎥
( f-n )
⎠
⎥⎦
(5.60)
As constantes da equações (5.59) são dadas por,
X 2 = X d''
X ''
( f-n ) q( f-n )
Td''
( f-n )
Ta
''
= Td0
( f-n )
( f-n ) =
X d''
( f-n )
+ X2 + X0
X d'
( f-n )
+ X2 + X0
2X2 + X0
2ra + r0
J.L.F. – Máquina Síncrona em Regime Transitório
b0 =
1
X 0 − X d''
+ X
( f-n ) 2 0
1
1
X q''
+ X 0 + X d''
+ X0
( f-n ) 2
( f-n ) 2
Td'
( f-n )
'
= Td0
( f-n )
X q''
1
( f-n ) + 2
X d'
( f-n )
+ X2 + X0
Xd
( f-n )
+ X2 + X0
(5.61)
2006
Capítulo 5 – Equações do Curto-Circuito
62
5.5 - Curto-Circuito Trifásico Assimétrico Fase-Fase-Neutro em Vazio
ia
A
in
Estator
N
B
C
ib
ib = 0
If
Rotor
Fig.5.59 - Esquema do curto circuito assimétrico Fase-Fase-Neutro
Em complemento do ensaio curto-circuito às três fases, fase com fase, fase com neutro,
considerados previamente, uma máquina síncrona poderá ter dois terminais simultaneamente
curto-circuitados ao neutro ou terra. Este curto-circuito é considerado também sem carga
jusante.
As condições de curto-circuito das duas fase A e C sem carga, de acordo com a
representação da figura 5.59 entre é,
ea = ec = 0
ib = 0
5.5.1 – Equações das Correntes nas Fases
Tal como foi abordado na análise do curto circuito fase-fase, fase-neutro a fase-faseneutro há a partilha do mesmo princípio teórico visto serem todos curtos-circuitos
assimétricos.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 5 – Equações do Curto-Circuito
63
Assim a equação da corrente do curto-circuito fase A ou fase C e o Neutro, representa-se
da seguinte forma,
entre a fase A e o neutro
U q ⎧ ⎡ ''
⎤
⎛
⎞
− ⎢3 X q
+ 2 X 0 ⎟ sen ( ωt ) ⎥ C +
ian
(t ) =
cos ( ωt ) − 3 ⎜ X q''
⎨
( f-f-n )
( f-f-n )
D ⎩ ⎣
⎝ ( f-f-n )
⎠
⎦
3 ⎡⎛
⎤
⎞
⎛ ''
⎞
''
+ ⎢⎜ X d''
+ X q'
⎟ cos ( ωt ) − ⎜ X d( f-f-n ) − X q( f-f-n ) ⎟ cos ( 2ωt − λ ) ⎥ A +
f-f-n
f-f-n
(
)
(
)
2 ⎣⎝
⎠
⎝
⎠
⎦
+
3 ⎡⎛ ''
⎞
⎛ ''
''
''
⎜ X d( f-f-n ) + X q( f-f-n ) + 4 X 0 ⎟ sen ( λ ) − ⎜ X d( f-f-n ) − X q( f-f-n )
⎢
2 ⎣⎝
⎠
⎝
⎤ ⎫
⎞
⎟ sen ( 2ωt − λ ) ⎥ B ⎬
⎠
⎦ ⎭
(5.62)
entre a fase C e o neutro
icn
( f-f-n )
(t ) =
U q ⎧ ⎡ ''
⎤
⎛ ''
⎞
⎨− ⎢3 X q( f-f-n ) cos ( ωt ) − 3 ⎜ X q( f-f-n ) + 2 X 0 ⎟ sen ( ωt ) ⎥ C +
D ⎩ ⎣
⎝
⎠
⎦
3 ⎡⎛
⎤
⎞
⎛
⎞
cos ( ωt ) − ⎜ X d''
cos ( 2ωt − λ ) ⎥ A +
+ ⎢⎜ X d''
+ X q''
− X q''
⎟
⎟
f-f-n
f-f-n
f-f-n
f-f-n
)
( )⎠
)
( )⎠
2 ⎣⎝ (
⎝ (
⎦
+
3 ⎡⎛ ''
⎤ ⎫
⎞
⎞
⎛ ''
''
''
⎜ X d( f-f-n ) + X q( f-f-n ) + 4 X 0 ⎟ sen ( λ ) − ⎜ X d( f-f-n ) − X q( f-f-n ) ⎟ sen ( 2ωt − λ ) ⎥ B ⎬
⎢
2 ⎣⎝
⎝
⎠
⎠
⎦ ⎭
(5.63)
onde as constantes das equações (5.62) e (5.63) são dadas por,
Taα
( f-f-n )
−
A=e
Xe =
=
X2 + 2X0
ra + 2r0
Taβ
( f-f-n )
t
−
Taα
( f-f-n )
=
B=e
X2
ra
t
Taβ
( f-f-n )
X2 X0
X2 + X0
⎛ X '' + X
e
C = ⎜1 − d
⎜ X' + X
d
e
⎝
(
⎞
⎟e
⎟
⎠
−
t
''
Td
( f-f-n )
''
⎛ X '' + X
⎞
e − Xd + Xe ⎟e
+⎜ d
⎜ X' + X
X d + X e ⎟⎠
e
⎝ d
)
(
)
−
D = 2 ⎡ X 0 X d'' + X q'' + X d'' X q'' − X 0 X d'' − X q'' cos ( 2ωt ) ⎤
⎢⎣
⎥⎦
J.L.F. – Máquina Síncrona em Regime Transitório
t
'
Td
( f-f-n )
+
X d'' + X e
Xd + Xe
(5.63)
2006
Capítulo 5 – Equações do Curto-Circuito
64
5.5.2 - Equação da Corrente de Campo
Para a corrente de excitação,
⎛ X − X'
d( f-f-n )
⎜ d
(t ) = if0 + if0 ⎜
if
'
( f-f-n )
⎜ X d( f-f-n )
⎝
t
⎡ −
⎞⎢ T'
⎛
Tkd
⎟ ⎢ d( f-f-n ) ⎜
− ⎜1 −
⎟ ⎢e
''
⎟⎢
⎜ Td( f-f-n )
⎠
⎝
⎢⎣
⎤
t
−
⎞ − t
⎥
T
a ( f-f-n )
Tkd
⎟ Td''
−
cos ( ωt ) ⎥
e
⎟e
''
⎥
Td
⎟
⎥
f-f-n
(
)
⎠
⎥⎦
(5.65)
Este capítulo centrou-se no desenvolvimento das equações que irão permitir fazer a
simulação matemática da máquina nos vários tipos de curto-circuitos que foram abordados.
Sem estas equações não era possível quantificar os valores da corrente de curto-circuito
que a máquina irá desenvolver na ocorrência durante a perturbação.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6
Capítulo 6 – Ensaio Laboratorial
Ensaio Laboratorial
65
Introdução
Para confirmar a validade das considerações teóricas dos capítulos anteriores, foi
montada uma bancada de ensaio no Laboratório de Máquinas Eléctricas da Faculdade de
Ciências e Tecnologia da Universidade Nova de Lisboa. Uma Máquina de Corrente Contínua
a funcionar com Motor foi acoplada pelo veio a uma Máquina Síncrona a funcionar como
Gerador.
Por forma a salvaguardar a integridade do equipamento, foram feitos ensaios com
valores muito abaixo dos nominais representados na “Chapa das Características”, sendo
condição suficiente para levar à obtenção de uma imagem do comportamento do sistema em
regime nominal.
6.1 - Equipamento para o Ensaio no Laboratório
6.1.1 - Bancada de Ensaios
A Máquina de Corrente Contínua tem as seguintes características de especificação,
U n = 220 V
N = 2100 rpm
I n = 6,2 A
U exc = 200 V
P = 1 kW
I exc = 0,24 A
A Máquina Síncrona ensaiada tem as seguintes características,
U nY/∆ = 380/220 V
N = 1500 rpm
I n = 1,5 / 2,6 A
cosϕ = 0,8
P = 0,8 KVA / 0,8 kW
U exc = 220 V
f = 50 Hz
I exc = 1,6 A max.
Todos os ensaios foram obtidos com a bancada de ensaios ligada conforme o esquema
na figura 6.1. A velocidade de sincronismo do sistema foi possível de manter durante todos os
ensaios, com base na utilização da pistola estroboscópica, tal com representa a mesma figura.
O método de acerto da velocidade de sincronismo resultava assim numa coordenação entre
frequência estroboscópica referenciada no acoplamento dos veios das duas máquinas e a
regulação da alimentação e excitação da Máquina de Corrente Contínua, bem com a regulação
da corrente de excitação de campo do alternador.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
66
m.
r.p.
Uf
U exc
A
A
U2 V2 W2
I exc
If
G
M
3~
U1
A
V1
A
W1
A
N
A
0 - 220Vcc
S
Fig. 6.1 - Esquema de ligações da bancada de ensaios
6.1.2
- Equipamento de Medida
Para que este trabalho fosse possível foi necessário recorrer a equipamento de medida
convencional, tal como Voltímetros e Amperímetros, mas para obter as medidas dos curtoscircuitos reais, foi necessário recorrer a outro tipo equipamento de medida mais sofisticado.
Assim as curvas obtidas só foram possíveis com instrumentação de aquisição rápida de
sinal, o instrumento de medida utilizado foi o osciloscópio digital com uma largura de banda
de 300 Mhz ligado a quatro pinças amperimétricas de alta sensibilidade da marca Tektronix.
O modelo de osciloscópio com quatro entradas, satisfez em pleno a aquisição das
correntes de curto-circuito. No caso do curto-circuito trifásico simétrico foram adquiridas as
correntes das três fases e corrente de excitação em simultâneo.
As curvas das três fases e a de excitação visualizadas no écran, foram transformadas em
pontos, descrevendo todo o andamento temporal. Os pontos das curvas por sua vez deram
origem a ficheiros tipo texto (*.txt) e foram extraídos do osciloscópio através de uma
disquete. Toda a reconstituição gráfica foi finalmente feita e exposta nos itens seguintes.
A fotografia e características deste equipamento podem ser consultadas em Anexo e a
imagem do écran obtida durante o curto-circuito trifásico simétrico pode ser visualizada na
figura 6.5.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
67
6.2 - Ensaio Experimental para Obtenção das Características em Vazio e CurtoCircuito
ia
A
Estator
N
B
C
ic
ib
If
Rotor
Fig. 5.1 - Esquema do curto-circuito franco às três fases
No modelo do circuito equivalente por fase existem três parâmetros que são necessários
determinar, são eles, a resistência da armadura Ra , a reactância síncrona e a f.e.m. em vazio
por fase E0 . A resistência da armadura Ra , foi determinada pelo método volt-amperimétrico
em corrente contínua, está representada na figura 6.4 , enquanto a reactância síncrona e a
f.e.m. induzida foram determinadas pelo ensaio em circuito aberto e curto-circuito,
representado na figura 6.2.
O ensaio de circuito aberto foi realizado com a máquina síncrona animada com uma
velocidade síncrona nominal de 1500 r.pm., enquanto os enrolamentos do estator estavam em
circuito aberto. Varia-se a corrente de excitação de campo e mede-se a tensão de saída dos
enrolamentos do estator. A relação entre os terminais do enrolamento do estator e a corrente
de excitação de campo no rotor, permite obter a característica da máquina síncrona em vazio.
O ensaio em curto-circuito foi iniciado com uma corrente de campo regulada com um
reóstato para o mínimo, os terminais do estator foram curto-circuitados nos terminais das
três fases U1, V1 e W1, através do comutador S, intercalando em série os amperímetros onde
vai ser lida a corrente de curto-circuito da armadura como está representado na figura 6.1.
A representação de amperímetros no esquema, de facto são pinças amperimétricas que
lêem a corrente que passa em cada condutor, porque estes caso fossem amperímetros normais
sem qualquer transformador, estes seriam destruídos durante o curto-circuito devido às
elevadas corrente.
Antes do início do estudo do comportamento da máquina em curto-circuito, foi estudada
a característica em vazio e em curto-circuito à velocidade nominal. Com este estudo foram
obtidos todos os valores que possibilitaram a construção do gráfico da figura 6.2.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
68
3
350
Tensão de saída em vazio Eo(V)
300
Linha de Entreferro
E0 = 220V
250
Característica em
Vazio
2,5
I cc = f (if )
200
2
1,5
150
Característica em
Curto-Circuito
100
1
0,5
50
Icc=0,74A
In
1,39
1,2
1,07
0,97
0,89
0,81
0,72
0,63
0,55
0,46
0,36
0,28
0,16
0
0
0
Corrente de campo If (A)
Fig. 6.2 – Característica em vazio e curto-circuito @ 1500 rpm
A característica da reactância síncrona foi obtida com base no gráfico da figura 6.2, tendo
por base a seguinte equação,
E0 = U + jX d I
E0 = X d I
(6.1)
considerando, U = 0 em (5.1) , então E0 = X d I , assim,
E
Xd = 0
I cc
(6.2)
O gráfico abaixo, da figura 6.3 foi construído com base na equação (6.2), para valores
coincidentes de corrente de campo I f . O dados que possibilitaram as construção dos gráficos
podem ser consultados em Anexo I. Este gráfico permite situar o valor da reactância síncrona
a partir do ponto de funcionamento da máquina, sabendo-se a corrente de campo I f à
velocidade nominal.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Corrente de Curto-Circuito Icc (A)
E0 = f (if )
Capítulo 6 – Ensaio Laboratorial
69
700
Xd =
Reactância Sincrona Xd (Ohms)
600
E0
I cc
500
400
X d = f ( If )
300
200
100
1.75
1.59
1.5
1.39
1.3
1.2
1.14
1.01
0.91
0.81
0.7
0.61
0.51
0.41
0.36
0.3
0.23
0.19
0.12
0.1
0
0
Corrente de cam po If(A)
Fig. 6.3 – Característica da reactância síncrona @ 1500 rpm
Tal como descrito em 5.1.3. o gráfico da figura 5.4 foi obtido experimentalmente
recorrendo ao método volt-amperimétrico.
O dados que possibilitaram a construção do gráfico podem ser consultados no Anexo
I.
80
ra =
Tensão na resistência da Amadura
Ua (V)
70
60
Ua
Ia
50
ra = 70Ω
40
30
20
10
0
0
0.2
0.4
0.6
0.8
1
1.2
Corrente na resistência da Arm adura
Ia (A)
Fig. 6.4 – Característica da resistência da armadura pelo método Volt- Amperimétrico
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
70
6.3 - Ensaio em Curto-Circuito Simétrico Entre as Três Fases
Fig. 6.5 – Imagem do écran do osciloscópio gravada no instante em que foi feito o
curto-circuito simétrico trifásico e adquirido pelos seus 4 canais.
Depois do tratamento dos dados gerados pelo osciloscópio em formato *.TXT estes
foram transformados em curvas através do programa Excel tal como pode ser observado nas
figuras seguintes,
968
924
880
836
792
748
704
660
616
572
528
484
440
396
352
308
264
220
176
132
88
44
0
Ia (A )
1,5
1,0
0,5
0,0
-0,5
-1,0
ia ( A ) -1,5
-2,0
-2,5
-3,0
-3,5
-4,0
-4,5
t (ms)
t (ms)
Fig. 6.6 - Corrente de curto-circuito trifásico simétrico - Fase A
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
71
968
924
880
836
792
748
704
660
616
572
528
484
440
396
352
308
264
220
176
132
88
44
0
Ib (A)
3,0
2,5
2,0
1,5
1,0
ib ( A ) 0,5
0,0
-0,5
-1,0
-1,5
-2,0
-2,5
t t(ms)
(ms)
Fig. 6.7 - Corrente de curto-circuito trifásico simétrico - Fase B
3,0
2,5
2,0
1,5
Ic (A)
1,0
0,5
ic ( A ) 0,0
-0,5
-1,0
-1,5
-2,0
968
924
880
836
792
748
704
660
616
572
528
484
440
396
352
308
264
220
176
132
88
44
0
-2,5
(ms)
t t(ms)
Fig. 6.8 - Corrente de curto-circuito trifásico simétrico - Fase C
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
72
1,8
1,6
1,4
1,2
1,0
0,8
0,6
0,4
0,2
0,0
974
912
851
790
731
670
609
547
486
425
366
305
244
182
121
60
0
-0,2
tt (ms)
(ms)
Fig. 6.9 - Corrente de excitação de campo durante o curto-circuito trifásico simétrico
6.3.1 – Simulação de Cálculo das Correntes de Curto-Circuito
Uma vez obtidos os gráficos pelo ensaio da máquina em Laboratório, através deles é
possível extrair as variáveis necessárias para proceder à simulação gráfica. Assim tendo como
base os gráficos da figura 6.6 até à 6.9, obtidos directamente pelo ensaio em curto-circuito,
mediante uma análise gráfica detalhada é possível determinar outras variáveis fundamentais.
Fazendo uma redução no período temporal dos gráficos das figuras supra mencionadas,
de 200ms para 100ms, para melhor enquadrar toda a oscilação imediatamente após o curto
circuito, obtêm-se consequentemente as figuras 6.10, 6.11 e 6.12.
5.0
4.0
3.0
2.0
1.0
Ia (A)
ia ( A )
0.0
-1.0
-2.0
-3.0
-4.0
-5.0
-6.0
192
176
160
144
128
112
96
80
64
48
32
16
-7.0
0
If (A)
if ( A )
tt (ms)
(ms)
Fig. 6-10 - Envolvente da curva de curto-circuito trifásico simétrico - Fase A
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
73
5.0
4.0
3.0
2.0
Ib (A)
1.0
ib ( A )
0.0
-1.0
-2.0
-3.0
-4.0
176
192
176
192
160
144
128
t (ms)
t (ms)
112
96
80
64
48
32
16
0
-5.0
Fig. 6-11 - Envolvente da curva de curto-circuito simétrico - Fase B
5,0
4,0
3,0
2,0
Ic (A)
1,0
ic ( A )
0,0
-1,0
-2,0
-3,0
-4,0
160
144
128
112
96
80
64
48
32
16
0
-5,0
t t(ms)
(ms)
Fig. 6-12 - Envolvente da curva de curto-circuito simétrico - Fase C
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
74
Os contorno da envolvente destas figuras serve de base para a determinação do valor
médio do comportamento da envolvente subtransitória e transitória juntas, como se pode
observar nas figuras 6.13 e 6.14.
10,0
3,68
Td' = 45ms
I d'' = 3.68 A
I ''d+I'd(A)
I d' = 1.8 A
I d'
= 1.1A
e
1,10
1,0
0,74
I d = 0.74 A
1 '
Td
2
100
96
92
88
84
80
76
72
68
64
60
56
52
48
44
40
36
32
28
24
20
16
12
8
4
0
0,1
t (ms)
t (ms)
Fig. 6-13 - Curva envolvente subtransitória e transitória
10,0
3,68
I d''
= 1,36 A
e
I'' (A)
1,0
0,1
Td'' = 4,5 ms
0,0
0
4
8
12
16
20
24
28
32
36
40
t t (ms)
(ms)
Fig. 6-14 - Curva envolvente subtransitória
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
75
A figura 6.15 representa as componentes contínuas de cada corrente de fase, fazendo uma
tangente a cada curva, obtém-se uma intersecção das três rectas na origem. O ponto obtido é a
constante de tempo da armadura.
2
1
I aDC ,
0
-1
-2
Ta=40ms
-3
100
96
92
88
84
80
76
72
68
64
60
56
52
48
44
40
36
32
28
24
20
16
12
8
4
-4
0
I cDC
I (A)
I bDC , (A)
tt (ms)
(ms)
Fig. 6.15 - Componentes contínuas das três fases
A partir destes oscilogramas representados nas figuras 6.13, 6.14 e 6.15 obtém-se os
valores das constantes de tempo da máquina Td'' , Td' e Ta e as correntes I d'' e I d' .
Com base nas características da máquina mencionadas pelo seu fabricante na “Chapa de
Características” juntamente com as variáveis até aqui obtidas por ensaio esta máquina é
caracterizada pela seguinte tabela.
- Potência aparente fornecida pelo Alternador S = 800 VA
- Tensão nominal na saída do Alternador
U n = U q = 220 V
- Corrente nominal do Alternador
I n = 1,5 A
- Velocidade Síncrona do Alternador
N = 1500 r.p.m.
- Frequência da rede
- Corrente subtransitória do eixo directo
f = 50 Hz
- Corrente transitória do eixo directo
I d' = 1,8 A
- Corrente síncrona do eixo directo
I d = 0,74 A
- Constante de tempo transitória
Td' = 40 ms
- Constante de tempo subtransitória
Td'' = 4,5 ms
- Constante de tempo da armadura
Ta = 40 ms
J.L.F. – Máquina Síncrona em Regime Transitório
I d'' = 3,68 A
2006
Capítulo 6 – Ensaio Laboratorial
76
Para se poder fazer a simulação das correntes de curto-circuito vão ser calculados os
valores das reactâncias X d'' , X d' e X d .
Tendo por base os valores nominais da tensão e corrente nominais, consequentemente a
reactância nominal é,
Xn =
U n 220
=
I n 1,5
X n = 147 Ω
Pelo gráfico da figura 6.4, é possível obter a resistência da armadura,
ra = 70 Ω
Tendo por base as curvas da figura 6.2 é possível obter graficamente pela intersecção da
curva de tensão em vazio com a curva da corrente em curto circuito as seguintes variáveis
fundamentais, para o cálculo da reactância síncrona do eixo directo.
Tensão nominal em vazio
E0 = 220 V
Corrente de curto-circuito
Icc = I d = 0,74A
Corrente de campo
I f = 0,73 A
Assim com base na equação (6.2) e substituindo as variáveis acima mencionadas, obtémse,
E
220
Xd = 0 =
= 297 Ω
I cc
1,5
Reactância síncrona
X d = 297 Ω
Este resultado pode confirmar-se com a curva característica da reactância síncrona
representada na figura 6.3.
Com base nas variáveis determinadas graficamente pelo curto-circuito trifásico simétrico
é possível obter as reactâncias subtransitória e transitória da seguinte forma,
Uq
X d'' = '' =60 Ω
Id
Reactância subtransitória
X d'' = 60 Ω
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
77
Uq
X d' = ' = 122 Ω
Id
Reactância transitória
X d' = 122 Ω
Convertendo para unidades “pu” (por unidade) para que a máquina em estudo seja mais
facilmente comparada com outras similares que existem.
Xd
X d'
( pu )
( pu )
=
X d 297
=
= 2 pu
X n 147
=
X d' 122
=
= 0,83 pu
X n 147
X d''
60
''
=
=
= 0,41 pu
Xd
( pu ) X n 147
Substituindo as constantes acima achadas nas equações (5.36), (5.37) e (5.38) das
correntes de curto-circuito já deduzidas no capítulo anterior, obtém-se os andamentos
temporais para cada fase,
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
78
6.3.1 –Simulação de Cálculo das Correntes de Curto-Circuito
Simulação da corrente de curto-circuito na Fase A
Usando a seguinte equação,
t
t
⎡
−
− ⎤
⎢ U q ⎛ U q U q ⎞ Td' ⎛ U q U q ⎞ Td'' ⎥
ia (t ) = ⎢
+⎜ ' −
+ ⎜ '' − ' ⎟ e
⎟e
⎥ cos ( ωt + λ ) −
⎜X
⎟
⎜X
⎟
X
X
X
d
d
⎢
⎥
d⎠
⎝ d
⎠
⎝ d
⎣
⎦
t
t
⎛
⎞
−
−
U
U
q
q
⎜
⎟
Ta
Ta
e
e
cos ( λ ) +
cos ( 2ωt + λ ) ⎟
−⎜
X
X
n
⎜ m
⎟
⎝
⎠
(5.36)
Resulta o gráfico da figura 6.16,
200
0
Ia (A)
ia ( A ) 200
400
600
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
t (s)
(s)
Fig. 6.16 - Corrente de curto-circuito trifásico na fase A simulada.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
79
Simulação da corrente de curto-circuito na Fase B
Usando a seguinte equação,
t
t
⎡
−
− ⎤
⎛
⎞
⎛
⎞
'
Uq Uq
Uq Uq
⎢ Uq
2π ⎞
⎛
T
T '' ⎥
ib (t ) = ⎢
+⎜ ' −
⎟ e d + ⎜ '' − ' ⎟ e d ⎥ cos ⎜ ωt + λ −
⎟−
⎜X
⎟
⎜X
⎟
X
X
3
⎝
⎠
X
d
d
⎢
⎥
d⎠
⎝ d
⎠
⎝ d
⎣
⎦
t
t
⎛
⎞
−
−
2π ⎞ U q Ta
2π ⎞ ⎟
⎛
⎛
⎜ U q Ta
e
e
cos ⎜ λ −
cos ⎜ 2ωt + λ −
−⎜
⎟+
⎟
3 ⎠ Xn
3 ⎠ ⎟⎟
⎝
⎝
⎜ Xm
⎝
⎠
(5.37)
Resulta o gráfico da figura 6.17,
400
Ib (A)
200
ib ( A ) 0
200
400
0
0.1
0.2
0.3
0.4
0.5
( s )
t (s)
0.6
0.7
0.8
0.9
1
t
Fig. 6-17 - Corrente de curto-circuito trifásico na fase B simulada.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
80
Simulação da corrente de curto-circuito na Fase C
Usando a seguinte equação,
t
t
⎡
−
− ⎤
⎛
⎞
⎛
⎞
Uq Uq
Uq Uq
⎢ Uq
4π ⎞
⎛
T'
T '' ⎥
+⎜ ' −
ic (t ) = ⎢
⎟ e d + ⎜ '' − ' ⎟ e d ⎥ cos ⎜ ωt + λ −
⎟−
⎜X
⎟
⎜X
⎟
X
X
3
⎝
⎠
X
d
d
⎢
⎥
d⎠
⎝ d
⎠
⎝ d
⎣
⎦
t
t
⎛
⎞
−
−
4π ⎞ U q Ta
4π ⎞ ⎟
⎛
⎛
⎜ U q Ta
−⎜
cos ⎜ λ −
cos ⎜ 2ωt + λ −
e
e
⎟+
⎟
3 ⎠ Xn
3 ⎠ ⎟⎟
⎝
⎝
⎜ Xm
⎝
⎠
(5.38)
Resulta o gráfico da figura 6.18,
Currente de Curto-Circuito Simétrico na Fase C
600
Ic (A)
400
ic ( A ) 200
0
200
0
0.1
0.2
0.3
0.4
0.5
tt (s)
(s)
0.6
0.7
0.8
0.9
1
Fig. 6.18 - Corrente de curto-circuito trifásico na fase C simulada.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
81
Simulação da Corrente de Campo,
Usando a seguinte equação,
⎛ X − X'
d
if (t ) = if0 + if0 ⎜ d
⎜ X'
d
⎝
⎡ − t
⎞⎢ T' ⎛ T
⎟ ⎢e d − ⎜1 − kd
⎟
⎜
Td''
⎠⎢
⎝
⎣
t
⎤
t
−
−
⎞ T '' T
⎥
⎟ e d − kd e Ta cos ( ωt ) ⎥
⎟
Td''
⎥
⎠
⎦
(5.46)
Resulta o gráfico da figura 6.19
6
4
If (A)
if ( A ) 2
0
2
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
t t (s)
(s)
Fig. 6.19 - Corrente de excitação de campo durante o curto-circuito simulada
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
82
Simulação das Componentes Contínuas
Usando as seguintes equações,
t
Uq − T
I a DC ( t ) =
e a cos ( λ )
Xm
t
Uq − T
2π ⎞
⎛
I b DC ( t ) =
e a cos ⎜ λ − ⎟
Xm
3 ⎠
⎝
t
Uq − T
4π ⎞
⎛
I c DC ( t ) =
e a cos ⎜ λ − ⎟
Xm
3 ⎠
⎝
Resulta o gráfico da figura 6.20
400
I c DC
200
I aDC ,
(A)
I bDC , I (A)
I b DC
0
I cDC
200
I a DC
400
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
t (s)
t (s)
Fig. 6.20 – Componentes contínuas das correntes de curto-circuito
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
83
Simulação da Segunda Harmónica de cada fase,
Fase A
100
50
⎛U − t
⎞
q
⎜
T
a
ia2H ( t ) =cos ( 2ωt + λ ) ⎟
e
⎜ Xn
⎟
⎝
⎠
0
50
100
Fase B
0
0.05
0.1
0.15
0.2
0.05
0.1
0.15
0.2
0.15
0.2
100
50
⎛U − t
⎞
2π ⎞
q
⎛
⎜
e Ta cos ⎜ 2ωt + λ − ⎟ ⎟
i b2H ( t ) =⎜ Xn
3 ⎠⎟
⎝
⎝
⎠
0
50
100
Fase C
0
t1
100
50
⎛U − t
⎞
4π ⎞
q
⎛
ic2H ( t ) =- ⎜
e Ta cos ⎜ 2ωt + λ − ⎟ ⎟
⎜ Xn
3 ⎠⎟
⎝
⎝
⎠
0
50
100
0
0.05
0.1
Pode-se observar que as segundas harmónicas das três fases são sub-amortecidas,
evidenciando uma sobrelevação no instante inicial, quando se dá o curto-circuito e depois
tende para zero até à sua extinção, coincidindo com a entrada da máquina em regime
permanente. A corrente de excitação do campo no ensaio representada na figura 6.9 e de
forma simulada na figura 6.19, à semelhança das correntes nas fases, sofre também uma
sobrelevação no instante inicial no período subtransitório e transitório, mas sempre sobre a
sua componente contínua, a qual tenderá a manter-se no regime nominal.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
84
6.4 - Ensaio em Curto-Circuito Assimétrico entre Duas Fases
Este é o primeiro tipo de curto-circuito assimétrico a ser analisado, o segundo é entre
duas fases e o terceiro é entre duas fases e o neutro. Este paralelismo apenas difere na
existência de impedâncias da máquina e qualquer outra impedância entre o neutro e a terra.
As fases que foram curto-circuitadas foram a C e a B, ficando a fase A em vazio.
ia = 0
A
ic = −ib
Estator
N
ic
C
B
ib
If
Rotor
Fig. 5.2 - Esquema do curto circuito assimétrico Fase-Fase
Os gráficos das figuras que se seguem foram obtidos da mesma forma que os do ensaio
anterior, aqui apenas vão ser abordados as duas fases que contribuíram para o curto circuito, a
fase A ficou em vazio como se pode observar na figura 5.2.
1,5
1,0
0,5
0,0
-0,5
( f-f ) (
A)
Ia (A)
-1,0
-1,5
-2,0
-2,5
-3,0
-3,5
-4,0
600
580
560
540
520
500
480
460
440
420
400
380
360
340
320
300
280
260
240
220
200
180
160
140
120
80
100
60
40
0
-4,5
20
ib
t
t (m s)
(ms)
Fig. 6.21 – Corrente de curto-circuito assimétrico fase-fase – Fase B
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
85
4,5
4,0
3,5
3,0
2,5
2,0
A
( f-f ) ( ) 1,5
Ic (A)
ic
1,0
0,5
0,0
-0,5
-1,0
600
580
560
540
520
500
480
460
440
420
400
380
360
340
320
300
280
260
240
220
200
180
160
140
120
100
80
60
40
20
0
-1,5
(m s)
t t(ms)
Fig. 6.22 – Corrente de curto-circuito assimétrico fase-fase – Fase C
2,0
1,5
If (A)
1,0
0,5
0,0
504
528
552
576
600
160
168
176
184
192
480
456
432
408
384
360
336
312
288
264
240
216
192
168
144
120
96
72
48
24
0
-0,5
(m s)
t t (ms)
Fig. 6.23 – Corrente de campo durante curto-circuito assimétrico fase-fase
2,0
1,0
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
200
152
144
136
128
120
112
104
96
88
80
72
64
56
48
40
32
24
16
8
-8,0
0
( f-f )
(A)
Ia (A)
ib
t (ms)
t (m s)
Fig. 6.24 - Envolvente da curva de curto-circuito da fase B
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
86
8,0
7,0
6,0
5,0
4,0
Ic (A)
A
( f-f ) ( )
ic
3,0
2,0
1,0
0,0
-1,0
200
192
184
176
168
160
152
144
136
128
120
112
104
96
88
80
72
64
56
48
40
32
24
16
8
0
-2,0
s)
tt (m(ms)
Fig. 6.25 - Envolvente da curva de curto-circuito da fase C
6.4.1 –Simulação de Cálculo das Correntes de Curto-Circuito
Através dos gráficos anteriores obtém-se as variáveis necessárias para proceder à
simulação gráfica. Assim tendo como base os gráficos das figuras 6.21 e 6.22 obtidos
directamente pelo ensaio em curto-circuito, mediante uma análise gráfica detalhada é possível
determinar outras variáveis fundamentais.
Fazendo uma redução no período temporal dos gráficos das figuras das envolventes, de
200ms para 100ms, para melhor enquadrar toda a oscilação imediatamente após o curto
circuito, obtêm-se assim as figuras 6.23 e 6.24.
Os contorno da envolvente das figuras 6.24 e 6.25 serve de base para a determinação do
valor médio do comportamento da envolvente subtransitória e transitória juntas, como se pode
observar nas figuras 6.26 e 6.27.
10
Id''
= 3,01 A
( f-f )
3,01
( f-f )
= 1,8 A
I''d+ I'd (A)
Id'
Td'
1
I d'
( f-f )
e
( f-f )
= 48 ms
= 1,1 A
1 '
Td
2 ( f-f )
0
0
4
8
12
16
20
24
28
32
36
40
44
48
52
56
60
64
68
72
76
80
84
88
92
96
100
t (ms)
t (ms)
Fig. 6.26 - Envolvente Subtransitória e Transitória
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
87
10,0
I d''
( f-f )
e
= 1,1 A
I'' (A )
1,0
0,1
Td''
= 2,5 ms
( f-f )
0,0
0
4
8
12
16
(ms)
t t (ms)
Fig. 6.27 – Envolvente Subtransitória
4
3
I ''d + I 'd (A )
2
1
0
-1
-2
Ta ( ) =58 ms
f-f
-3
-4
0
4
8
12
16
20
24
28
32
36
40
44
48
52
56
60
64
68
72
76
80
84
88
92
96
100
t t (ms
(ms)
)
Fig. 6.28 – Componentes continuas das duas fases
Através das figuras 6.26, 6.27 e 6.28 obtém-se os valores das constantes de tempo da
máquina Td''
( f-f )
, Td'
( f-f )
e Ta
( f-f )
e as correntes I d''
e I d'
, importantes para a
( f-f )
( f-f )
simulação matemática.
- Corrente subtransitória do eixo directo (fase-fase)
I d''
( f-f )
- Corrente transitória do eixo directo (fase-fase)
I d'
( f-f )
- Constante de tempo transitória (fase-fase)
Td'
- Constante de tempo subtransitória (fase-fase)
Td''
J.L.F. – Máquina Síncrona em Regime Transitório
( f-f )
( f-f )
= 3,01 A
= 1,1 A
= 48 ms
= 2,5 ms
2006
Capítulo 6 – Ensaio Laboratorial
88
- Constante de tempo da armadura (fase-fase)
Ta
( f-f )
= 58 ms
Para se poder fazer a simulação das correntes de curto-circuito vão ser calculados os
e X d'
.
valores das reactâncias X d''
( f-f )
( f-f )
O cálculo da reactância subtransitória entre fases tem por base os valores em cima
determinados,
X d''
( f-f )
=
Uq
I d''
( f-f )
= 73,1 Ω
X d''
( f-f )
= 73,1 Ω
Da mesma forma a reactância transitória entre fases fica,
X d'
( f-f )
=
Uq
I d'
( f-f )
= 200 Ω
X d'
( f-f )
= 200 Ω
Convertendo para unidades “pu” (por unidade) para que a máquina em estudo seja mais
facilmente comparada com outras similares que existem.
Xd
X d'
X d''
( pu )
( pu )
( pu )
=
=
=
X d 297
=
= 2 pu
X n 147
X d'
( f-f )
Xn
X d''
( f-f )
Xn
=
200
= 1,36 pu
147
=
59,78
= 0,50 pu
147
Substituindo as constantes acima achadas nas equações (5.55), (5.56), (5.57) e (5.58) das
correntes de curto-circuito já deduzidas no capítulo anterior, obtém-se os andamentos
temporais para cada fase.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
89
6.4.1 –Simulação de Cálculo das Correntes de Curto-Circuito
Simulação da corrente de curto-circuito entre fases da Fase B
Usando a seguinte equação,
t
⎡
−
'
⎢
⎛
⎞ T
d f-f
1
1
1
⎢
⎜
⎟
ib
e ( ) +
+⎜
−
(t ) = 3U q ⎢
⎟
( f-f )
X + X 2 ⎜ X d'
+ X2 Xd + X2 ⎟
⎢ d
( f-f )
⎝
⎠
⎢
⎣
⎛
⎞
1
1
⎜
⎟
+⎜
−
⎟e
''
'
+
+
X
X
X
X
⎜ d( f-f )
2
d( f-f )
2⎟
⎝
⎠
∞
× ∑ ( −b ) sen ( (2n − 1) ( ωt ) ) +
n
n=0
−
t
''
T
d( f-f )
(5.55)
×
3U q sen(λ ) ⎛ 1 ∞
⎞
n
⎜ + ∑ ( −b ) cos(2nωt ) ⎟ e
X2
⎝ 2 n =1
⎠
−
t
Ta
( f-f )
Resulta o gráfico da figura 6.29
200
0
( f-f ) (
ibff (A)
ib
A)
200
400
600
0
0.1
0.2
0.3
0.4
0.5
t (s)
(s)
0.6
0.7
0.8
0.9
1
Fig. 6.29 – Simulação do curto-circuito fase-fase – Fase B
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
90
Simulação da corrente de curto-circuito entre fase da Fase C
Usando a seguinte equação,
t
⎡
−
⎢
⎛
⎞ T'
d( f-f )
1
1
1
⎢
⎜
⎟
ic
e
+⎜
−
+
(t ) = − 3U q ⎢
( f-f )
X d + X 2 ⎜ X d'
X d + X 2 ⎟⎟
+
X
2
⎢
⎝ ( f-f )
⎠
⎢
⎣
t
−
⎛
⎞ T ''
d( f-f )
1
1
⎜
⎟
+⎜
−
×
e
⎟
''
'
⎜ X d( f-f ) + X 2 X d( f-f ) + X 2 ⎟
⎝
⎠
∞
(5.56)
−
× ∑ ( −b ) sen ( (2n − 1)(ωt) ) +
n
n=0
t
3U q sen(λ ) ⎛ 1 ∞
⎞ Ta ( f-f )
n
+
−
ω
b
n
cos(2
t)
∑
(
)
⎜
⎟e
X2
⎝ 2 n =1
⎠
Resulta o gráfico da figura 6.30
600
400
( f-f ) (
icff (A)
ic
A)
200
0
200
0
0.1
0.2
0.3
0.4
0.5
t t(s)(s)
0.6
0.7
0.8
0.9
1
Fig. 6.30 – Simulação do curto-circuito fase-fase – Fase C
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
91
Simulação da corrente de campo
Usando a seguinte equação,
⎛ X − X'
d( f-f )
⎜ d
if
(t ) = if0 + if0 ⎜
'
( f-f )
⎜ X d( f-f )
⎝
⎡ − t
⎞⎢ T'
⎛
T
⎟ ⎢ d( f-f ) ⎜
− ⎜1 − kd
⎟ ⎢e
''
⎟⎢
⎜ Td( f-f )
⎠
⎝
⎣⎢
⎤
t
−
⎞ − t
⎥
Ta
Tkd
⎟ Td''
f-f )
(
e
cos ( ωt ) ⎥
−
⎟e
''
⎥
Td
⎟
⎥
f-f
(
)
⎠
⎦⎥
(5.57)
Resulta o gráfico da figura 6.31
4
if
iFff (A)
2
( f-f ) (
A)
0
2
0
0.1
0.2
0.3
0.4
0.5
tt(s)
(s)
0.6
0.7
0.8
0.9
1
Fig. 6.31 – Simulação do curto-circuito fase-fase – Corrente de campo
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
92
Num curto-circuito simétrico constatam-se que as correntes, são praticamente sinosoidais,
tendo apenas a sobreposição de um termo de 2ª harmónica praticamente desprezável,
porque X d'' ≈ X q'' .
Isto é válido porque as equações de ia , ib , e ic foram deduzidas
considerando que há ausência de saturação na máquina.
Desprezado o termo da 2ª harmónica visto ser pequeno, podem ser observadas as
correntes de curto circuito admitindo saturação do circuito magnético. Contudo a saturação do
circuito magnético implica uma corrente de 3ª harmónica. Porém, se o curto circuito simétrico
se dá sem neutro a componente de 3ª harmónica não tem caminho por onde se fechar e
portanto as correntes não são sinosoidais.
As figuras seguintes ilustram as componentes de 2ª e 3ª harmónicas,
1
2.5
Resultante
Fundamental
Fundamental
Amplitude
Corrente (A)
0.5
0
2ª Harmónica
1.25
2ª Harmónica
0.5
1
0
1
2
3
4
Angulo (rad)
5
0
6
Fig. 6.32 – Comportamento das correntes de 1ª, 2ª
harmónicas e resultante
24
32
Fundamental
2
0.5
Amplitude
Fundamental
0
1.5
1
3ª Harmónica
3ª Harmónica
0.5
1
16
Espectro
2.5
Resultante
Corrente (A)
8
Fig. 6.33 - Espectro da 1ª e 2ª harmónicas
Corrente de 3 Harmónica
1
0
0.5
0
1
2
3
4
Angulo (rad)
5
Fig. 6.34 – Comportamento das correntes de 1ª, 3ª
harmónicas e resultante
J.L.F. – Máquina Síncrona em Regime Transitório
6
0
0
8
16
Espectro
24
32
Fig. 6.35 – Espectro de 1ª e 3ª harmónicas
2006
Capítulo 6 – Ensaio Laboratorial
93
6.5 - Ensaio em Curto-Circuito Assimétrico entre Fase e Neutro
ia
A
in
Estator
N
C
B
ic = 0
ib = 0
If
Rotor
Fig. 6.36 - Esquema do curto-circuito entre Fase - Neutro
Os gráficos das figuras que se seguem foram obtidos da mesma forma que os do ensaio
anterior, aqui apenas vai ser abordado a fase A e o neutro que contribuíram para o curto
circuito, a fase B e C ficaram em vazio como se pode observar na figura 6.36.
5
4
3
2
A
( f-n ) ( )
Ia (A)
1
0
-1
992
960
928
896
864
832
800
768
736
704
672
640
608
576
544
512
480
448
416
384
352
320
288
256
224
192
160
96
128
64
0
-2
32
ia
t (ms)
t (m s)
Fig. 6.37 – Corrente de curto-circuito entre fase e neutro – Fase Ia
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
94
12
10
8
6
( f-n )
(A)
If (A)
if
4
2
0
-2
992
960
928
896
864
832
800
768
736
704
672
640
608
576
544
512
480
448
416
384
352
320
288
256
224
192
160
96
128
64
0
32
-4
tt (ms)
(ms)
Fig. 6.38 - Corrente de curto-circuito entre fase e neutro – Corrente de campo If
7
6
5
4
ia
Ia (A)
3
A
( f-n ) ( )
2
1
0
-1
-2
200
192
184
176
168
160
152
144
136
128
120
112
104
96
88
80
72
64
56
48
40
32
24
16
8
0
-3
(m s )
t t (ms)
Fig. 6.39 - Envolvente da corrente de curto-circuito entre fase e neutro – Fase Ia
10.0
I d'' (f-n) = 2, 75 A
I d' (f-n) = 1,8 A
1.0
I d' (f-n)
e
= 1,1 A
1 '
Td
= 144 ms
2 ( f-n )
Td'
( f-n )
= 72 ms
200
192
184
176
168
160
152
144
136
128
120
112
104
96
88
80
72
64
56
48
40
32
24
16
8
0.1
0
I''d+I'd
t t(ms)
(ms)
Fig. 6.40 - Curva envolvente subtransitória e transitória
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
95
10
I d'' (f-n) = 2,75 A
I''d ( f-n )
e
= 1.01 A
1
I''d (A)
Td''
( f-n )
= 9 ms
0,1
0
4
8
12
16
20
24
28
32
t (ms)
Fig. 6.41 – Curva envolvente subtransitória
2,5
2,0
1,5
1,0
I (A)
0,5
0,0
-0,5
-1,0
Ta
-1,5
( f-n )
= 27 ms
-2,0
-2,5
0
4
8
12
16
20
24
28
32
36
40
44
48
52
56
60
64
68
72
76
80
84
88
92
96 100
t t (ms)
(ms)
Fig. 6.42 – Componente continua da fase A
Através das figuras 6.40, 6.41 e 6.42 obtém-se os valores das constantes de tempo da
máquina Td''
( f-n )
, Td'
( f-n )
e Ta
( f-n )
e as correntes I d''
e I d'
, importantes para a
( f-n )
( f-n )
simulação matemática.
- Corrente subtransitória do eixo directo (fase-neutro)
I d''
( f-n )
- Corrente transitória do eixo directo (fase-neutro)
I d'
( f-n )
- Constante de tempo transitória (fase-neutro)
Td'
- Constante de tempo subtransitória (fase-neutro)
Td''
J.L.F. – Máquina Síncrona em Regime Transitório
( f-n )
( f-n )
= 2,75 A
= 1,8 A
= 72 ms
= 9 ms
2006
Capítulo 6 – Ensaio Laboratorial
96
- Constante de tempo da armadura (fase-neutro)
Ta
( f-n )
= 27 ms
Para se poder fazer a simulação das correntes de curto-circuito vão ser calculados os
e X d'
.
valores das reactâncias X d''
( f-n )
( f-n )
O cálculo da reactância subtransitória entre fases tem por base os valores em cima
determinados,
X d''
( f-n )
=
Uq
I d''
( f-n )
= 80 Ω
X d''
( f-n )
= 80 Ω
Da mesma forma a reactância transitória entre fases fica,
X d'
( f-n )
=
Uq
I d'
( f-n )
= 122, 2 Ω
X d'
( f-n )
= 122, 2 Ω
Convertendo para unidades “pu” (por unidade) para que a máquina em estudo seja mais
facilmente comparada com outras similares que existem.
Xd
X d'
X d''
( pu )
( pu )
( pu )
=
=
=
X d 297
=
= 2 pu
X n 147
X d'
( f-n )
Xn
X d''
( f-n )
Xn
=
200
= 0,83 pu
147
=
59,78
= 0,55 pu
147
Substituindo as constantes acima achadas nas equações (5.59) e (5.60) das correntes de
curto-circuito já deduzidas no capítulo anterior, obtém-se os andamentos temporais para cada
fase.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
97
6.5.1 –Simulação de Cálculo das Correntes de Curto-Circuito
Simulação da corrente de curto-circuito fase-neutro - Fase A
Usando a seguinte equação,
t
⎡
−
⎞ T ''
⎢⎛
d( f-n )
1
1
⎜
⎟
−
+
(t ) = 3U q ⎢⎜
ia
e
⎟
⎢ X ''
( f-n )
+ X 2 + X 0 X d'
+ X2 + X0 ⎟
⎜
d
⎢⎝ ( f-n )
( f-n )
⎠
⎢⎣
⎛
1
1
⎜
+⎜
−
'
⎜ X d( f-n ) + X 2 + X 0 X d + X 2 + X 0
⎝
t
−
⎞ T'
⎤
d( f-n )
1
⎟
+
⎥×
⎟e
+
+
X
X
X
⎟
d
2
0 ⎥⎦
⎠
(5.59)
t
∞
⎞ − Ta
3U q cos(λ ) ⎛⎜ 1
n
n
×
+
( −b0 ) cos ( (2n − 1) ( ωt ) ) −
( −b0 ) cos(2nωt) ⎟⎟ e ( f-n )
⎜⎜ 2
1
⎟
X 2 + X0 ⎝
n=0
n =1
⎠
2
∞
∑
∑
Resulta o gráfico o gráfico da figura 6.41
800
600
( f-n ) (
IFN (A)
ia
400
A)
200
0
200
400
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
t (s)
(s)
Fig. 6.41 – Simulação da corrente de curto-circuito entre fase e neutro
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
98
Simulação do curto-circuito fase-neutro - Corrente de Campo
Usando a seguinte equação,
⎛ X − X'
d( f-n )
⎜ d
(t ) = if0 + if0 ⎜
if
'
( f-n )
⎜ X d( f-n )
⎝
⎡ − t
⎞⎢ T'
⎛
T
⎟ ⎢ d( f-n ) ⎜
− ⎜1 − kd
⎟ ⎢e
''
⎟⎢
⎜ Td( f-n )
⎠
⎝
⎢⎣
⎤
t
−
⎞ − t
⎥
Ta
Tkd
⎟ Td''
f-n )
(
−
cos ( ωt ) ⎥
e
⎟e
''
⎥
Td
⎟
⎥
f-n
( )
⎠
⎥⎦
(5.60)
Resulta o gráfico o gráfico da figura 6.42
4
if
iFfn (A)
3
( f-n ) (
2
A)
1
0
1
0
0.1
0.2
0.3
0.4
0.5
t (s)
(s)
0.6
0.7
0.8
0.9
1
Fig. 6.42 – Simulação do curto-circuito fase-neutro– Corrente de campo
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
99
Análise dos Oscilogramas das correntes de curto-circuito assimétrico fase-neutro e
fase-fase.
Considerando um curto-circuito entre uma só fase e o neutro, a corrente de curto-circuito
resultante é constituída por componentes do regime subtransitório, transitório e permanente
podendo representar-se da seguinte forma,
Estas componentes ao atravessarem a
I cc = I d''
+ I'
+I
( f-n ) d ( f-n ) d perm.( f-n )
fase A do estator vão produzir uma f.m.m.
oscilatória. Esta f.m.m. oscilatória de
(f.m.m. pulsante)
ω
frequência ω pode ser decomposta em duas
f.m.m.s girantes que rodam com a velocidade
−ω
+ω
icc
A
angular ω em sentidos contrários. A
(f.m.m.)1
Estator
N
(f.m.m.) 2
ω
no sentido do rotor (síncrono com ele) e a
(f.m..m.) 2
B
Φf
(f.m..m.)1 roda com a velocidade angular +ω
Curto - Circuito
Fase - Neutro
−ω
(com uma
velocidade 2 ω relativa ao rotor).
C
⎛ Velocidade
⎜
⎜ angular do
⎜ rotor
⎝
no sentido
⎞
⎟
⎟
⎟
⎠
A
(f.m..m.)1 , rodando síncrona com o rotor
induz no enrolamento de campo apenas uma
componente contínua, visto que a amplitude
da (f.m..m.)1 decai no tempo Td''
( f-n )
Rotor
Td'
+2f
( f-n )
A
if
.
(f.m..m.) 2 ,
rodando
com
uma
de 2 ω em relação ao rotor, induz
no enrolamento de campo componentes
alternadas de frequência 2f (2ª harmónica).
Estas componentes alternadas de 2f do
rotor, produzem por sua vez uma f.m.m.
pulsante de frequência 2f, que se podem
decompor em duas f.e.m.s girantes, de
(f.m.m.)1' velocidade
-2f
(f.m.m.)'2
Fig. 6.43 – Esquema da máquina durante o
curto circuito Fase-Fase
2f
⎛ f.m.m. ⎞
⎜
⎟
⎝ pulsante ⎠
velocidade angular 2 ω relativas ao rotor, em sentidos contrários assinalados na figura por
(f.m..m.)1' e (f.m..m.)'2 .
A (f.m..m.)1' girando com a frequência 2f no sentido de rotação do rotor vai por sua vez
induzir no estator uma corrente de frequência 2f + f = 3f ou seja a 3ª harmónica.
A (f.m..m.)'2 girando com a frequência -2f em sentido contrário à rotação do rotor irá por
sua vez induzir no estator uma corrente de frequência -2f + f = -f , isto é, com o valor absoluto
da fundamental.
J.L.F. – Máquina Síncrona em Regime Transitório
e
2006
Capítulo 6 – Ensaio Laboratorial
100
Conclusão:
No curto-circuito assimétrico faseω
neutro, mesmo com o circuito magnético
−ω
+ω
A
linear, obtêm-se correntes de 2ª harmónica
no rotor e de 3ª harmónica no estator,
(f.m.m.) 2
(f.m.m.)1
Curto - Circuito
Porém, o processo repete-se. A corrente
Fase - Fase
Estator
de 3ª harmónica do estator, por sua vez,
N
induz uma corrente de 4ª harmónica no rotor
B
C
e esta reflecte-se no estator com uma
icc
corrente de 5ª harmónica e assim
Φf
sucessivamente.
ω
De modo geral pode-se dizer que no
curto-circuito fase-neutro resultam uma série
⎛ Velocidade ⎞
de harmónicas pares no rotor e uma série de
⎜
⎟
⎜ angular do ⎟
Rotor
⎜ rotor
⎟
harmónicas ímpares no estator. Porém, esta
⎝
⎠
+2f
série é rapidamente convergente e na prática
pode considerar-se apenas as harmónicas de 2ª
if
(f.m.m.)1'
e 3ª como as mais importantes, podendo-se
-2f
considerar as outras harmónicas de ordem
superior desprezáveis.
2f
No caso do curto-circuito entre fases,
(f.m.m.)'2
⎛ f.m.m. ⎞
⎜
⎟
mantém-se toda a sequência acima descrita
⎝ pulsante ⎠
porque as f.m.m.s. pulsantes em cada fase em
Fig. 6.44 – Esquema da máquina durante o
curto circuito Fase-Fase
curto-circuito estão em fase, como se pode
observar na figura 6.44.
(f.m.m. pulsante)
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
101
Ensaio em curto-circuito entre duas fase e neutro
Análise dos Oscilogramas das correntes de curto-circuito
ia
A
.
in
Estator
N
ib
C
B
ib = 0
If
Rotor
Fig. 5.59 - Esquema do curto circuito assimétrico Fase - Fase-Neutro
1,0
0,5
0,0
-0,5
-1,0
( f-f-n ) (
A ) -1,5
Iac (A)
-2,0
-2,5
-3,0
-3,5
-4,0
972
936
900
864
828
792
756
720
684
648
612
576
540
504
468
432
396
360
324
288
252
216
180
144
108
72
36
-4,5
0
ian
tt (ms)
(ms)
Fig. 6.45 – Corrente de curto-circuito assimétrico fase-fase-neutro – Fase A e C
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
102
2
1
0
-1
( f-f-n ) (
A)
IN (A)
icn
-2
-3
-4
-5
-6
-7
-8
-9
972
936
900
864
828
792
756
720
684
648
612
576
540
504
468
432
396
360
324
288
252
216
180
144
108
72
36
0
-10
tt (ms)
(ms)
Fig. 6.46 – Corrente de curto-circuito assimétrico fase-fase-neutro – Fase C e Neutro
0,7
0,6
0,5
0,4
A
( f-f-n ) ( )
IF (A)
if
0,3
0,2
0,1
0,0
-0,1
-0,2
960
920
880
840
800
760
720
680
640
600
560
520
480
440
400
360
320
280
240
200
160
120
80
40
0
-0,3
tt (ms)
(ms)
Fig. 6.47 – Corrente de curto-circuito assimétrico fase-fase-neutro – Corrente de Excitação
1,5
0,5
-0,5
-1,5
-2,5
-3,5
-4,5
96
92
88
84
80
76
72
68
64
60
100
t t (ms)
(ms)
56
52
48
44
40
36
32
28
24
20
16
12
8
-5,5
4
A)
0
( f-f-n ) (
Iac (A)
ian
Fig. 6.48 – Envolvente da curva de curto-circuito assimétrico fase-fase-neutro – Fase A C
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
103
4,0
3,0
2,0
1,0
0,0
-1,0
A)
IN (A)
( f-f-n ) (
-4,0
-5,0
-6,0
-7,0
-8,0
-9,0
-10,0
-11,0
100
96
92
88
84
80
76
72
68
64
60
56
52
48
44
40
36
32
28
24
20
16
12
8
4
0
-12,0
t t(ms)
(ms)
Fig. 6.49 – Envolvente da curva de curto-circuito assimétrico fase-fase-neutro – Fase C e Neutro
10,0
( f-f-n )
= 5,25 A
Id'
= 2,8 A
I''d+I'd (A)
I d'
( f-f-n )
( f-f-n)
e
= 1,7 A
1,0
1 '
T
2 d ( f-f-n )
Td' ( f-f-n ) = 8 ms
60
56
52
48
44
40
36
32
28
24
20
16
12
8
0
0,1
4
I d''
(ms)
t t (ms)
Fig. 6.50 – Envolvente subtransitoria e transitória
10,0
I d''
( f-f-n )
e
I''(A)
icn
-2,0
-3,0
= 1,93 A
1,0
Td''
( f-f-n )
= 4 ms
0,1
0
4
8
12
16
t t(ms)
(ms)
Fig. 6.51 – Envolvente subtransitória
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
104
4,00
2,00
I (A)
0,00
-2,00
-4,00
Ta
-6,00
( f-f-n )
= 18 ms
-8,00
0
4
8
12
16
20
24
28
32
36
40
44
48
52
56
60
t (ms)
t (ms)
Fig. 6.52 – Componentes contínuas das fases A C e neutro
Através das figuras 6.40, 6.51 e 6.52 obtém-se os valores das constantes de tempo da
máquina Td''
( f-f-n )
, Td'
( f-f-n )
e Ta
( f-f-n )
e as correntes I d''
e I d'
, importantes para a
( f-f-n )
( f-f-n )
simulação matemática.
- Corrente subtransitória do eixo directo (fase-fase-neutro)
I d''
( f-f-n )
- Corrente transitória do eixo directo (fase-fase-neutro)
I d'
( f-f-n )
- Constante de tempo transitória (fase-fase-neutro)
Td'
- Constante de tempo subtransitória (fase-fase-neutro)
Td''
= 4 ms
- Constante de tempo da armadura (fase-fase-neutro)
Ta
= 18 ms
( f-f-n )
( f-f-n )
( f-f-n )
= 5,25 A
= 2,8 A
= 8 ms
Para se poder fazer a simulação das correntes de curto-circuito vão ser calculados os
e X d'
.
valores das reactâncias X d''
f-f-n
( )
( f-f-n )
O cálculo da reactância subtransitória entre fases tem por base os valores em cima
determinados,
X d''
( f-f-n )
=
Uq
I d''
( f-f-n )
= 59,78 Ω
J.L.F. – Máquina Síncrona em Regime Transitório
X d''
( f-f-n )
= 59,78 Ω
2006
Capítulo 6 – Ensaio Laboratorial
105
Da mesma forma a reactância transitória entre fases fica,
X d'
( f-f-n )
=
Uq
I d'
( f-f-n )
= 78,6 Ω
X d'
( f-f-n )
= 78,6 Ω
Convertendo para unidades “pu” (por unidade) para que a máquina em estudo seja mais
facilmente comparada com outras similares que existem.
Xd
X d'
X d''
( pu )
( pu )
( pu )
=
=
=
X d 297
=
= 2 pu
X n 147
X d'
( f-f-n )
Xn
X d''
( f-f-n )
Xn
=
200
= 0,54 pu
147
=
59,78
= 0,41 pu
147
Substituindo as constantes acima achadas nas equações (5.62), (5.63) e (5.65 ) das
correntes de curto-circuito já deduzidas no capítulo anterior, obtém-se os andamentos
temporais para cada fase,
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
106
Usando a seguinte equação,
ian
( f-f-n )
(t ) =
U q ⎧ ⎡ ''
⎤
⎛ ''
⎞
⎨− ⎢3 X q( f-f-n ) cos ( ωt ) − 3 ⎜ X q( f-f-n ) + 2 X 0 ⎟ sen ( ωt ) ⎥ C +
D ⎩ ⎣
⎝
⎠
⎦
3 ⎡⎛
⎤
⎞
⎛
⎞
+ ⎢⎜ X d''
+ X q'
− X q''
cos ( ωt ) − ⎜ X d''
cos ( 2ωt − λ ) ⎥ A +
⎟
⎟
f-f-n
f-f-n
f-f-n
f-f-n
)
( )⎠
)
( )⎠
2 ⎣⎝ (
⎝ (
⎦
+
3 ⎡⎛ ''
⎞
⎛ ''
''
''
⎜ X d( f-f-n ) + X q( f-f-n ) + 4 X 0 ⎟ sen ( λ ) − ⎜ X d( f-f-n ) − X q( f-f-n )
⎢
2 ⎣⎝
⎠
⎝
⎤ ⎫
⎞
⎟ sen ( 2ωt − λ ) ⎥ B ⎬
⎠
⎦ ⎭
(5.62)
Resulta o gráfico da figura 6.53
0
200
( f-f-n ) (
IAN (A)
ian
A)
400
600
800
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
tt (s)
(s)
Fig. 6.53 - Simulação da corrente de curto-circuito fase-fase-neutro - Fase A e Neutro
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
107
Usando a seguinte equação,
icn
( f-f-n )
(t ) =
U q ⎧ ⎡ ''
⎤
⎛ ''
⎞
⎨− ⎢3 X q( f-f-n ) cos ( ωt ) − 3 ⎜ X q( f-f-n ) + 2 X 0 ⎟ sen ( ωt ) ⎥ C +
D ⎩ ⎣
⎝
⎠
⎦
3 ⎡⎛
⎤
⎞
⎛ ''
⎞
''
+ ⎢⎜ X d''
+ X q''
⎟ cos ( ωt ) − ⎜ X d( f-f-n ) − X q( f-f-n ) ⎟ cos ( 2ωt − λ ) ⎥ A +
f-f-n
f-f-n
(
)
(
)
2 ⎣⎝
⎠
⎝
⎠
⎦
+
3 ⎡⎛ ''
⎞
⎛ ''
''
''
⎜ X d( f-f-n ) + X q( f-f-n ) + 4 X 0 ⎟ sen ( λ ) − ⎜ X d( f-f-n ) − X q( f-f-n )
⎢
2 ⎣⎝
⎝
⎠
⎤ ⎫
⎞
⎟ sen ( 2ωt − λ ) ⎥ B ⎬
⎠
⎦ ⎭
(5.63)
Resulta o gráfico da figura 6.54
0
200
( f-f-n ) (
ICN (A)
icn
A)
400
600
800
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
tt (s)
(s)
Fig. 6.54 - Simulação da corrente de curto-circuito fase-fase-neutro - Fase C e Neutro
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 6 – Ensaio Laboratorial
108
Para a corrente de excitação,
Usando a seguinte equação,
⎛ X − X'
d( f-f-n )
⎜ d
(t ) = if0 + if0 ⎜
if
'
( f-f-n )
⎜ X d( f-f-n )
⎝
t
⎡ −
⎞⎢ T'
⎛
Tkd
⎟ ⎢ d( f-f-n ) ⎜
− ⎜1 −
⎟ ⎢e
''
⎟⎢
⎜ Td( f-f-n )
⎠
⎝
⎢⎣
⎤
t
−
⎞ − t
⎥
T
a ( f-f-n )
Tkd
⎟ Td''
−
cos ( ωt ) ⎥
e
⎟e
''
⎥
Td
⎟
⎥
f-f-n
(
)
⎠
⎥⎦
(5.65)
Resulta o gráfico da figura 6.55
10
8
( f-f-n ) (
IF (A)
if
A)
6
4
2
0
2
0
0.1
0.2
0.3
0.4
0.5
t (s)
(s)
0.6
0.7
0.8
0.9
1
Fig. 6.55 - Simulação do curto-circuito fase-fase-neutro – Corrente de campo
As simulações realizadas neste capítulo permitem ter a percepção dos picos de corrente a
que o estator estaria sujeito caso se tratasse de um curto-circuito real em qualquer uma das
três possibilidades aqui estudadas. Assim, com base neste estudo pode-se iniciar todo o
dimensionamento das protecções de toda a carga a jusante, sejam disjuntores ou fusíveis.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 7 – Comportamento Dinâmico
109
Capítulo 7
Comportamento Dinâmico
7.1 - Comportamento do Binário durante o Curto-Circuito
As máquinas síncronas quando sujeitas a um curto–circuito, ficam sujeitas a esforços
dinâmicos importantes, originando o aparecimento de um binário perigoso, podendo danificar
o equipamento.
No decorrer do normal funcionamento da máquina existe uma igualdade entre a
velocidade mecânica do rotor e a velocidade de campo do estator.
Quando surge uma instabilidade motivada por um curto-circuito, esta relação é
perturbada, consequentemente a velocidade instantânea desce ligeiramente tal como a ângulo
de carga, aqui surge um binário. Para recuperar a velocidade síncrona, vão surgir oscilações
em torno da posição final, que tendem a anularem-se à medida que os enrolamentos
amortecedores dissipam as f.e.m. nele induzidas e tal como se pode observar na figura. 7.1.
Estas oscilações do binário tendem a extinguirem-se à medida que a máquina entra no
regime permanente.
Através da equação fundamental (5.50) do comportamento do binário e substituindo as
constantes da máquina obtidas no ensaio de curto-circuito simétrico franco no Capitulo 6
nesta equação, obtém-se o gráfico da figura 7.1.
T (t ) = U q 2e
+
t
Uq2 −T
a
T (N.m)
T (N)
.
4
e
1.5 .10
5
1 .10
5
5 .10
4
−
t
Ta
t
⎡
−
⎢ 1 ⎛ 1
1 ⎞ Td' ⎛ 1
1
sen ( ωt ) ⎢ ' + ⎜ ' −
+ ⎜ '' − '
⎟e
⎜
⎟
⎜X
⎢ Xd ⎝ Xd Xd ⎠
⎝ d Xd
⎣
t ⎤
−
⎞ T'' ⎥
⎟e d ⎥ +
⎟
⎥
⎠
⎦
(5.50)
⎛ 1
1 ⎞
sen ( 2ωt ) ⎜ '' − '' ⎟
⎜ Xd Xq ⎟
⎝
⎠
0
5 .10
4
1 .10
5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
t t (s)
(s)
Fig. 7.1 – Comportamento do Binário durante o curto-circuito.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 7 – Comportamento Dinâmico
110
7.1.1 – Determinação dos Parâmetros Mecânicos
A modelação mecânica da máquina síncrona completa-se com a determinação do valor
numérico dos seus parâmetros, estes podem ser obtidos por cálculo e por ensaio. No primeiro
caso é necessário saber o comportamento dos órgãos, dimensões, condições de funcionamento
que raramente se dispõe. No segundo caso por ensaio, podem-se obter os parâmetros de forma
mais realista.
7.1.2 – Cálculo do Momento de Inércia do rotor
Considere-se uma massa elementar dm situada à distância r de um ponto 0, como indica
figura 7.2 .
dm
r
0
Fig. 7.2 – Momento de inércia de uma massa
Denomina-se momento de inércia da massa dm colocada à distância r do centro de
rotação 0 tem, por definição, um momento polar de inércia infinitesimal dado pela relação
dJ = r 2 dm
Considere-se que o rotor tem um diâmetro Do e um comprimento axial l e uma massa
específica uniforme γ . O momento de inércia de um anel de espessura elementar dr e
comprimento axial l à distância r do centro de rotação tem o volume elementar dV = 2πrdrl
e a massa elementar dm = γdV .
l
dr
ω
γ
Fig. 7.3 - Rotor
J.L.F. – Máquina Síncrona em Regime Transitório
r
Do
γ
Ro
Fig. 7.4 - Vista em corte do rotor
2006
Capítulo 7 – Comportamento Dinâmico
111
De acordo com as figuras 7.3 e 7.4, por definição o momento polar do anel elementar
vale,
dJ = r 2 dm = r 2 γ 2πr λdr = γ 2πλr 3dr
(7.1)
assim o momento polar de inércia do rotor será,
R
⎡ r4 ⎤ 0 1
J=
dJ = γ 2πλ
r dr =γ 2πλ ⎢ ⎥ = γπλR04
2
⎢⎣ 4 ⎥⎦ 0
0
0
∫
R0
∫
R0
3
(7.2)
Sabendo-se que a massa do rotor vale m = γπλR02 , substituindo em (7.2) vem,
R02
⎛R ⎞
J =m
= m ⎜ 0 ⎟ = mRg2
2
⎝ 2⎠
(7.3)
R
onde o raio de giração Rg = 0 = 0,707 R0 representa a distância ao centro de uma coroa
2
infinitesimal .
Em termos práticos, na literatura e manuais técnicos, é normal explicitar o momento de
inércia J em termos de peso do rotor P = mg e do diâmetro de giração Dg = 2 Rg , podendo
finalmente representar-se por,
J=
1
PDg2 com
4g
g = 9,8 m/s 2
(7.4)
πD02
λg diâmetro de giração por
O peso do rotor pode ainda ser representa por P = γ
4
D
Dg = 0 .
2
O momento polar de inércia depende do raio do rotor à 4ª potência e é apenas
directamente proporcional ao seu comprimento axial. Nas máquinas com o mesmo volume
prismático V prism = D02 λ , que é equivalente a ter o mesmo binário T = kD02 λ o momento de
inércia é,
J=
1
γπV prism D02
32
( Kg .m2 )
J.L.F. – Máquina Síncrona em Regime Transitório
(7.5)
2006
Capítulo 7 – Comportamento Dinâmico
112
O momento de inércia da equação (7.5), varia com o quadrado do diâmetro. Daí que os
turboalternadores tenham um momento polar de inércia menor do que o dos hidroalternadores
para as mesmas condições. Pode-se observar a figura 1.5 e 1.6 que expõe em detalhe as
diferenças físicas entre ambos os tipos de máquinas síncronas.
7.1.3 – Métodos para Determinar o Momento de Inércia
Após desenvolvimento das equações do momento de inércia, é possível estudar o
comportamento dinâmico da máquina síncrona depois de ser desligada até que o seu
movimento fique completamente extinto.
Existem três processos para determinar a curva de desaceleração da velocidade de
andamento da máquina tendo como base o prévio cálculo do momento de inércia. Por ordem
crescente de fiabilidade existem os seguintes métodos:
•
Método analítico
Basta substituir os valores de catálogo de PDg2 directamente na equação (7.4) e
imediatamente se obtém o momento de inércia J.
•
Método do Pêndulo
Este método é mais preciso que o anterior porque é baseado na simulação real do
movimento pendular através da extracção do rotor do interior da máquina.
Uma vez o rotor extraído, o seu veio vai ser colocado sobre duas barras que se pretendem
com o mínimo de atrito, para não perturbar o movimento pendular que lhe vai ser imposto. O
movimento pendular vai ser conseguido com auxílio de um peso colocado a uma distância de
preferência ao centro de massa do rotor, seguidamente anima-se o sistema.
O momento de inércia que vai ser obtido depende do tempo que o sistema demora a
parar, que se deve à relação das diferenças entre as massas do rotor e do peso.
•
Método da medição do Atrito
Este método é mais prático porque leva à obtenção de resultados práticos de forma
directa, através da simulação de desaceleração do rotor. Esta simulação é feita com a máquina
na sua aplicação normal, consiste em desligar o accionamento mecânico quando esta se
encontra na velocidade síncrona e registar todos os pontos de velocidade até que pare em
zero.
Todos estes pontos reunidos permitem a obtenção da curva de desaceleração.
Assumindo que a máquina síncrona está animada com uma velocidade síncrona e
subitamente lhe é desligado o acoplamento mecânico, que a acciona, este fenómeno é definido
pela seguinte equação,
J
d ωr
= −Tf
dt
J.L.F. – Máquina Síncrona em Regime Transitório
(7.6)
2006
Capítulo 7 – Comportamento Dinâmico
113
λ
r
γ
ω
θ
mg
Pêndulo
Fig. 7.5 – Medição do momento de inércia pelo Método do Pêndulo
Na equação 7.6, Tf é o binário de fricção devido à existência de fricção nas escovas,
rolamentos e bobinagem.
Assumindo que as condições de atrito viscoso são dados pela seguinte equação,
Tf = Kb
Kb ωr
r
(7.7)
Obtém-se assim a equação da velocidade angular do rotor,
ωr = ωm e
−
t
τem
(7.8)
a qual mostra a desaceleração do rotor sobre condição de atrito viscoso apresentando um
andamento exponencial decrescente.
Desde que o momento de inércia seja J seja conhecido, o binário de fricção Tf para uma
dada velocidade deverá ser avaliado a partir da curva de desaceleração como se pode observar
na Fig. 7.6.
1500
N (rpm)
1000
500
0
0
1
2
3
4
5
t(s)
Fig. 7.6 – Curva de desaceleração do rotor
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 8 – Conclusões Finais
Capítulo 8
Conclusões Finais
114
O presente trabalho é uma ferramenta muito importante para poder prever as correntes
que as máquinas síncronas de pólos salientes podem atingir quando sujeitas a um brusco
curto-circuito. Para o efeito, foram identificados os ensaios que são considerados mais críticos
para a integridade física da máquina e equipamento envolvente.
Para conhecer a presente máquina foi necessário fazer vários ensaios, a fim de conhecer
as suas características fundamentais tais como curva da f.e.m. em vazio, curva da corrente de
armadura em curto-circuito, reactâncias e constantes de tempo, deduzidas a partir das curvas
das correntes de curto-circuito obtidas em ensaio com correntes de tensões reduzidas,
comparativamente com os valores nominais definidos pelo fabricante da máquina.
As constantes de tempo e reactâncias determinadas pertencem aos três períodos temporais
onde se enquadra um curto-circuito típico, que são o subtransitório, transitório e nominal.
Com o conhecimento destas constantes, foi possível simular graficamente o andamento
temporal das correntes de curto-circuito que a máquina irá desenvolver quando for sujeita a
um brusco curto-circuito em regime nominal.
Estas curvas simuladas irão ajudar no dimensionamento das protecções do circuito a
jusante, visto poderem ser confrontadas com as curvas das protecções e assim será possível
escolher a protecção mais adequada. De salientar que o valor eficaz da corrente subtransitória
alcançada durante os dois primeiros ciclos, serve como base para o cálculo da corrente de
regulação da interrupção do disjuntor a seleccionar para proteger a carga aplicada à máquina.
Os ensaios desenvolvidos, possibilitaram o confronto entre a teoria da máquina síncrona e
os respectivos resultados experimentais, que se revelaram estar em quase absoluta sintonia,
evidenciada graficamente.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo 8 – Conclusões Finais
Capítulo 9
Trabalho Futuro
115
Toda a vasta Teoria exposta sobre esta matéria exige a avaliação comportamental da
máquina num exaustivo conjunto de situações diferenciadas ao nível de simulações, que este
trabalho procurou de forma modesta abordar através da selecção criteriosa das consideradas
críticas para análise do fenómeno.
No entanto, a investigação desenvolvida, os resultados obtidos e a actualidade da
temática no contexto da segurança dos sistemas de produção de energia, onde se insere a
máquina estudada, estimulam a um aprofundamento de alguns assuntos, nomeadamente o
comportamento do binário da máquina durante o curto-circuito.
A continuidade deste trabalho está assim, desde já assegurada pela motivação para a
“descoberta” de soluções que protejam os grandes centros produtores de energia de ameaças
ao seu funcionamento e que são passíveis de desenvolvimento no campo experimental e
teórico.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Capítulo10
Capítulo 8 – Conclusões Finais
Bibliografia
116
[1] Bernard Adkins M.A.. “ The General Theory of Electrical Machines”. Chapman an Hall,
1964, ISBN 412 07840 6/87
[2] Charles Concordia “Synchronous Machines Theory and Performance”. General Electric
Company, 1951. Chapter 4, 5 , 6, 7.
[3] Chee – Mun Ong, “Dynamic Simulation of Electric Machinery, using MatLab
/Simulink”. Prentince Hall, ISBN 0-13-723785-5. Chapter 7 –Synchonous Machines
[4] Syed A. Nasar, “Máquinas Eléctricas” . Schaum McGraw-Hill, CEP 04533 . Capítulo 6 –
Máquinas Síncronas.
[5] A.E. Fitzgerald, “Máquinas Eléctricas”. McGraw –Hill, Capítulo 10 – Máquinas de C.A.,
Transitórios e Dinâmica
[6] Siemens, “Manual de Engenharia Eléctrica” Livraria Nobel S.A. - Nº0536, Capítulo 8 –
Corrente de Curto-Circuito em sistemas trifásicos.
[7] A. Leão Rodrigues, “Conversão Electromecância de Energia – Máquina Síncrona”
Universiade Nova de Lisboa, Faculdade de Ciências e Tecnologia, Departamento de
Engenharia Electrotécnica.
[8] Stephen J. Chapman, “ Electric Machinery Fundamentals” McGraw-Hill - Synchronous
Motors
[9] A. J. Ellison, “Electromechanical Energy Conversion” Engineering Science Monographs
– George G. Harrap & Co. LTD, 1965 ISBN 245 55845 - Chapter 7
[10] J. Chatelain, “Machines Électriques” Dunod – 1983 ISBN 2-04-015620-8 – Chapitre 7
[11] Catálogos da ABB - AMG Synchronous Generators for Power Plants
[12] Catálogos da Siemens
[13] Catálogos da General Electric
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Anexos
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Reactância síncrona
do eixo directo
I cc (A)
Icc(A)
X d (Ω)
Xd(Oh)
Corrente
Corente
de excitação
excitação If(A)
I f (A)
campo
dede
campo
J.L.F. – Máquina Síncrona em Regime Transitório
5
0
1,75 142,79 2,05 293
1,59 151,14 1,91 289
1,50 168,82 1,71 289
1,39 169,01 1,65 279
1,30 195,81 1,43 280
1,20 193,00 1,40 270
1,14 211,70 1,26 267
1,01 232,49 1,12 260
0,91 249,99 1,00 250
0,81 270,55 0,86 233
0,70 295,70 0,74 219
0,61 302,00 0,65 196
0,51 323,09 0,52 168
0,41 360,08 0,38 137
0,36 362,16 0,33 120
0,02
0,12
55
0,17
0,23
0,86
1,00
Resultados que serviram de base à construção do gráfico da figura 6.3.
2006
250
Resultados Experimentais
0,91
246
242
0,87
0,89
238
0,83
233
231
0,79
0,81
228
225
0,74
0,77
221
0,72
219
208
0,67
0,70
203
0,65
0,74
190
0,59
196
185
0,57
0,65
179
0,55
0,61
178
0,53
168
162
0,48
0,51
152
0,46
137
148
0,52
0,38
129
120
0,44
0,41
0,39
0,33
109
0,34
0,36
99
0,32
91
80
0,28
0,30
69
0,25
0,25
43
0,10
32
20
15
5
0,19
0,16
0,14
0,01
0,10
Anexos
0,30 362,58 0,25 91
0,23 323,53 0,17 55
0,19 430,00 0,10 43
0,12 577,35 0,02 12
0,10 472,38 0,01
0
E0 (V)
E0(V)
590,00
Circuito Aberto
@1500 r.p.m
Curto-Circuito
@1500 r.p.m
0
•
0
saída
Tensão de saida
em Circuito Aberto E0 (V)
@1500 r.p.m
Corrente de
I cc (A)
Curto-Circuito
@1500 r.p.m
Correntede
de
Corente
de
I f (A)
eexcitação
xciação de
campo
campo
0
•
0
Anexo I
118
Resultados que serviram de base à construção do gráfico da figura 6.2.
Período
Periodo
I aDC (A)
Componentes
Componentes
Contínuas
I bDC (A)
continuas
I cDC (A)
J.L.F. – Máquina Síncrona em Regime Transitório
8
0,15 -0,20 -0,80 100
0,20 -0,19 -0,80 96
0,26 -0,17 -0,80 92
1,06 100
1,08 96
1,10 92
1,12 88
1,13 84
1,15 80
0,32 -0,16 -0,80 88
1,18 72
1,20 68
1,22 64
1,23 60
1,26 56
1,30 52
1,33 48
1,36 44
1,42 40
1,49 36
1,54 32
1,62 28
1,76 24
1,90 20
2,08 16
2,28 12
2,57
1,16 76
• Resultados que serviram de base à construção do gráfico das figura 6.15
0,35 -0,13 -0,80 84
0,38 -0,10 -0,80 80
0,41 -0,12 -0,80 76
0,44 -0,04 -0,80 72
0,47 -0,01 -0,80 68
0,50 0,02 -0,80 64
0,53 0,05 -0,80 60
0,56 0,08 -0,80 56
0,60 0,11 -0,80 52
0,65 0,12 -0,75 48
0,70 0,15 -0,72 44
0,75 0,15 -0,69 40
0,85 0,20 -0,66 36
0,85 0,25 -0,63 32
1,00 0,30 -0,60 28
1,00 0,40 -0,85 24
1,00 0,30 -1,10 20
1,00 0,40 -1,30 16
1,00 0,40 -1,70 12
8
t ( ms )
1,10 0,60 -2,10
I d'' + I d' (A)
4
Média
t ( ms )
0,90 0,70 -2,90
ra(o)
ra ( Ω )
68,18 1,10
70,00 1,00
66,33 0,98
66,67 0,90
67,07 0,82
66,67 0,75
67,16 0,67
66,67 0,60
67,31 0,52
66,67 0,45
66,67 0,39
68,57 0,35
68,75 0,32
66,67 0,30
69,23 0,26
69,57 0,23
70,00 0,20
70,59 0,17
71,43 0,14
72,73 0,11
75,00 0,08
76,92 0,05
90,91 0,02
75
70
65
60
55
50
45
40
35
30
26
24
22
20
18
16
14
12
10
8
6
4
2
0
Resistência
da Armadura
0
Ia(A)
I a (A)
4
Corrente da
Armadura
2,95
U a (A)
Ua(V)
0
Tensão da
Armadura
0,80 1,00 -3,75
Período
Periodo
0
•
3,68
Anexos
119
Resultados que serviram de base à construção do gráfico da figura 6.4.
• Resultados que serviram de base à construção dos gráficos das figuras 6.13 e 6.14.
2006
Periodo
Período
t ( ms )
Componente
Componente I
aDC ( f-n ) (A)
Continua
Contínua
J.L.F. – Máquina Síncrona em Regime Transitório
8
4
-1,26 1,40 88
-1,25 1,38 92
-1,23 1,36 96
-1,21 1,34 100
0,047 88
0,038 92
0,029 96
0,020 100
-1,30 1,44 80
-1,32 1,46 76
-1,28 1,42 84
1,25 100
1,25 96
1,29 92
-1,34 1,48 72
-1,36 1,50 68
1,33 84
1,29 88
-1,38 1,52 64
-1,40 1,54 60
-1,42 1,56 56
-1,44 1,58 52
-1,46 1,60 48
-1,48 1,62 44
-1,50 1,66 40
-1,55 1,68 36
-1,55 1,75 32
-1,60 1,90 28
-1,65 1,90 24
-1,75 1,90 20
-1,70 2,00 16
-1,90 2,00 12
-2,05 2,13
-2,38 2,15
0
1,33 80
1,36 76
1,35 72
1,38 68
Resultados que serviram de base à construção do gráfico das figuras 6.40 e 6.41
0,056 84
0,065 80
0,074 76
0,083 72
0,092 68
0,101 64
0,110 60
0,119 56
1,40 64
0,128 52
1,45 56
1,45 52
1,48 48
1,50 44
1,50 40
1,53 36
1,55 32
1,63 28
1,70 24
1,75 20
1,85 16
2,03 12
1,42 60
Resultados que serviram de base à construção do gráfico da figura 6.42
0,137 48
0,146 44
0,155 40
0,200 36
0,300 32
0,500 28
0,600 24
0,800 20
1,000 16
1,200 12
8
I d'' ( f-n ) + I d' ( f-n ) (A)
8
Média
2,15
t ( ms )
4
Periodo
Período
1,300
•
I cDC ( f-f ) (A)
2,39
•
I aDC ( f-f ) (A)
4
Componentes
Componentes
Contínuas
continuas
t ( ms )
1,500
Periodo
Período
-3,50 3,50
•
8
4
0
1,30 100
1,31 96
1,32 92
1,33 88
1,35 84
1,37 80
1,39 76
1,41 72
1,43 68
1,45 64
1,47 60
1,49 56
1,51 52
1,53 48
1,55 44
1,58 40
1,61 36
1,65 32
1,75 28
1,78 24
1,83 20
1,85 16
1,95 12
2,09
2,26
3,50
I d'' ( f-f ) + I d' ( f-f ) (A)
0
Média
t ( ms )
2,75
Periodo
Período
0
•
2,000
Anexos
120
Resultados que serviram de base à construção dos gráficos das figuras 6.26 e 6.27.
Resultados que serviram de base à construção do gráfico da figura 6.28
2006
8
Componentes
Componentes
Contínuas
continuas
t ( ms )
I aDC ( f-f-n ) (A)
-5,00 1,39
Periodo
Período
4
I cDC ( f-f-n ) (A)
J.L.F. – Máquina Síncrona em Regime Transitório
-0,70 0,33 60
-0,64 0,33 56
-0,52 0,25 52
-0,58 0,33 48
-0,63 0,29 44
-0,78 0,25 40
-1,02 0,40 36
-1,26 0,51 32
-1,67 0,46 28
-1,87 0,66 24
-2,31 0,64 20
-2,96 0,93 16
I d'' ( f-f-n ) + I d' ( f-f-n ) (A)
-3,60 1,10 12
•
-5,50 1,86
Média
8
4
0,33 100
0,34 96
0,36 92
0,37 88
0,39 84
0,40 80
0,42 76
0,43 72
0,45 68
0,46 64
0,48 60
0,49 56
0,51 52
0,52 48
0,54 44
0,54 40
0,56 36
0,57 32
0,59 28
0,60 24
1,72 20
1,78 16
1,78 12
1,93
2,83
0
t ( ms )
5,25
Periodo
Período
0
•
-7,00 3,02
Anexos
121
Resultados que serviram de base à construção do gráfico da figura 6.50 e 6.51
Resultados que serviram de base à construção do gráfico da figura 6.52
2006
Anexos
Anexo II
122
Instrumentação de Medida
Pinça amperimétrica usada na medida das
correntes de curto-circuito.
Exemplo da forma como as correntes de curtocircuito foram obtidas.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Anexos
123
Osciloscópio digital de 4 canais usado na medida das correntes de curto-circuito.
Especificações
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Largura de Banda 300 MHz
Taxa de amostragem acima de 5 GS/s
4 canais
Cinescópio de fósforo colorido VGA
Disquete de interface para e disco duro para armazenamento de dados e configurações
21 tipos de medidas automáticas
Porta paralelo tipo Centronics
9-Bit de resolução vertical
Suporta configuração para várias línguas
Menu de utilização rápido
Trigger avançado nos 4 canais
Transformadas rápidas de Fourier (FFT) para análise de frequência e de harmónicas
Módulo de saída de video
Suporta pontas activas, pontas diferenciais e pontas de corrente que possiblitam escala
automática.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Anexo III
Anexos
Fotografias da Bancada de Ensaios
124
Bancada de ensaios com a máquina de Corrente contínua de accionamento
à esquerda e a máquina síncrona trifásica à direita e comutador ao centro.
Grande plano da máquina de corrente contínua de accionamento
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Anexos
125
Grande plano da máquina síncrona trifásica
Painel de controlo, protecções, regulação das correntes de excitação das
máquinas, correntes e tensões de armadura.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Anexos
126
Taquímetro estroboscópico manual, que possibilitou fazer todos os
testes à velocidade nominal de forma estável.
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Anexo IV
Curto-Circuito Simétrico
200
Ia (A)
0
200
400
600
0
01
02
03
04
05
06
07
08
09
1
0
01
02
03
04
05
06
07
08
09
1
200
6 0
01
02
03
04
05
06
07
08
09
1
0.1
0.2
0.3
0.4
0.5
t (s)
0.6
0.7
0.8
0.9
1
400
Ib (A)
200
0
200
400
600
Ic (A)
400
200
0
If (A)
4
2
0
2
0
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Anexo V
Curto-Circuito Assimétrico Fase-Fase
200
ibff (A)
0
200
400
600
0
600
01
02
03
04
05
06
07
08
09
1
01
02
03
04
05
06
07
08
09
1
0.1
0.2
0.3
0.4
0.5
t (s)
0.6
0.7
0.8
0.9
1
icff (A)
400
200
0
200
4 0
iFff (A)
2
0
2
0
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Anexo VI
Curto-Circuito Assimétrico Fase-Neutro
800
600
IAfn (A)
400
200
0
200
400
4 0
01
02
03
04
05
06
07
08
09
1
0.1
0.2
0.3
0.4
0.5
t (s)
0.6
0.7
0.8
0.9
1
iFfn (A)
3
2
1
0
1
0
J.L.F. – Máquina Síncrona em Regime Transitório
2006
Curto-Circuito Assimétrico
Fase-Fase-Neutro
Anexo VII
0
ICN (A)
200
400
600
800
0 0
01
02
03
04
05
06
07
08
09
1
0
01
02
03
04
05
06
07
08
09
1
0
0.1
0.2
0.3
0.4
0.5
t (s)
0.6
0.7
0.8
0.9
1
ICN (A)
200
400
600
800
10
8
IF (A)
6
4
2
0
2
J.L.F. – Máquina Síncrona em Regime Transitório
2006