delineando convergências entre investigação temática e

DELINEANDO CONVERGÊNCIAS ENTRE
INVESTIGAÇÃO TEMÁTICA E MODELAGEM
MATEMÁTICA
Ana Paula dos Santos Malheiros
UNESP, Brasil
[email protected]
RESUMO
Este texto apresenta as aproximações existentes entre a Modelagem em
Educação Matemática e as Investigações Temáticas, propostas por Paulo
Freire. A partir de um estudo bibliográfico, baseado no paradigma
qualitativo, a pesquisa mostra como as ideias e pressupostos acerca das
Investigações Temáticas convergem para a Modelagem, principalmente nas
concepções baseadas na perspectiva sociocrítica, pautada na Educação
Matemática Crítica, principalmente quando o tema eleito para o trabalho faz
parte do cotidiano e/ou da realidade dos alunos. O estudo evidencia diversas
aproximações entre a Investigação Temática e a Modelagem e ressalta que
em ambas se busca, além da construção do conhecimento por meio do
diálogo, a reflexão e o despertar da consciência crítica dos educandos e dos
educadores.
Palavras-chave: Paulo Freire. Educação Matemática Crítica. Educação
Matemática.
ABSTRACT
This paper presents existing approaches between the Modeling in
Mathematics Education and the Thematic Researches, proposed by Paulo
Freire. From a bibliographical study, based on the Qualitative Paradigm, the
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
research shows how the ideas and assumptions about the Thematic Research
converge on Modeling, mainly on concepts from the social critic
perspective, based on the Critical Mathematics Education, especially when
the chosen theme for the work is part of the students´ daily lives and/or their
reality. The study reveals several links between the Thematic Research and
Modeling and highlights that not only the construction of knowledge
through dialogue is sought in both, but also the reflection and awakening of
critical consciousness of learners and educators.
Key-words: Paulo Freire. Critical Mathematics Education.
Mathematics Education.
1
Introdução
A Modelagem1, no contexto da Educação Matemática, teve início no século XX
(BARBOSA, 2001), quando matemáticos puros e aplicados discutiam métodos para se
ensinar Matemática. No Brasil, seu surgimento, de acordo com Borba e Villarreal
(2005), ocorreu a partir das ideias e trabalhos de Paulo Freire e de Ubiratan
D’Ambrosio, na década de 1970, os quais valorizavam aspectos sociais em salas de
aula. Biembengut (2009) também destaca que a Modelagem, no cenário da Educação
Matemática, no Brasil, surgiu quase que no mesmo período que em outros países,
principalmente pela atuação dos professores Aristides Barreto, Ubiratan D’Ambrosio,
Rodney Bassanezi, João Frederico Meyer, Marineuza Gazzetta e Eduardo Sebastiani.
Na década de 1980, a Modelagem ganhou força por meio da influência dos
trabalhos do professor D’Ambrosio – orientador do professor Bassanezi, quem conduziu
os principais trabalhos da área - que ministrava aulas e orientava trabalhos tanto na
UNESP quanto na UNICAMP (ARAÚJO, 2010; BORBA; VILLARREAL, 2005), além
de proporcionar cursos para a formação de professores em serviço. Foi neste período
que ela se consolidou como abordagem pedagógica no Brasil e, desde então, diversos
estudos sobre Modelagem na Educação Matemática têm surgido. Ainda, nos últimos
anos, é notório o aumento de pesquisas acerca dessa tendência em Educação
1
Nesse texto Modelagem e Modelagem Matemática serão utilizados como sinônimos, evitando assim
possíveis repetições.
2
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
Matemática (BIEMBENGUT, 2009).
Nesse contexto, a Modelagem vem sendo investigada e discutida enquanto
abordagem pedagógica por pesquisadores como Barbosa (2001; 2003; 2007), Araújo
(2002, 2007; 2009; 2010), Bassanezi (2002), Borba (2002; 2009), Malheiros (2004;
2008; 2012), dentre tantos outros2. Nesses trabalhos, uma das principais características
da Modelagem consiste em lidar com “problemas abertos”, sendo um de seus objetivos
é resolver uma situação “qualquer” com auxílio da Matemática.
Se olharmos para parte da literatura da Educação Matemática, as concepções de
Modelagem encontradas diferenciam-se em alguns aspectos e o que as distingue,
basicamente, é a ênfase na escolha do problema a ser investigado, que pode partir do
professor, pode ser um acordo entre professor e alunos ou então os estudantes podem
escolher o assunto que pretendem investigar. Além disso, é possível considerar que elas
possuem um objetivo comum: investigar e/ou pesquisar e/ou resolver problemas da
realidade (seja ela do estudante, da escola, da comunidade) utilizando, para isso,
conhecimentos matemáticos.
Ainda, se continuarmos a investigar a literatura existente, encontramos autores
(ARAÚJO, 2009; JACOBINI; WODEWOTZKI, 2006; BARBOSA, 2003) que afirmam
que dentre as diferentes concepções de Modelagem existentes no contexto da Educação
Matemática, há aquelas que podem ser classificadas de acordo com a perspectiva
sociocrítica, que tem como base os trabalhos de Paulo Freire, Ubiratan D’Ambrosio e
Ole Skovsmose, prioritariamente.
Porém, em um levantamento bibliográfico 3 realizado recentemente no Brasil,
encontrei apenas o trabalho de Forner (2005), que menciona a obra de Freire e a
Modelagem concomitantemente. Sua pesquisa investigou as influências da obra de
Paulo Freire na formação de professores de Matemática, a partir de entrevistas com
renomados educadores matemáticos nacionais. Nesse trabalho, o autor evidencia que há
relação entre a Modelagem e o pensamento freireano e alguns de seus entrevistados
também mencionam influências de Freire na Etnomatemática e na Modelagem,
principalmente. Entretanto, elas não são explicitadas no trabalho.
Também encontrei trabalhos que relacionam a perspectiva dialógica de Paulo
2
Nesse texto não será realizada uma revisão de literatura aprofundada sobre Modelagem em Educação
Matemática, visto que tal fato não é foco do mesmo.
3
Tal levantamento foi realizado no bando de teses da CAPES e também nos principais periódicos da área,
ao longo do primeiro semestre de 2011.
3
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
Freire explicitamente com a Educação Matemática Crítica (EMC), como o de Silva
(2007). Nele, a autora apresenta interlocuções existentes entre EMC e a perspectiva
dialógica, com o foco na formação dos professores de Matemática.
Recentemente, em Meyer, Caldeira e Malheiros (2011, p.15), escrevemos que
“[...] podemos traçar um paralelo entre a filosofia de educação de Paulo Freire e o
trabalho escolar com a Modelagem Matemática de fenômenos de interesses de seus
alunos e de suas comunidades”.
Nesse sentido, considerando que parte da comunidade que pesquisa Modelagem
evidencia a influência de Paulo Freire na Modelagem, de modo direto ou indireto,
comecei a me debruçar com maior interesse sobre sua obra, com intuito de tentar
melhor compreender de que maneira tal fato aconteceu. Ao longo dos estudos
realizados, me deparei com as Investigações Temáticas (FREIRE, 2005), publicadas na
obra Pedagogia do Oprimido, na década de 1960. Assim, nesse texto, de cunho teórico,
apresento as aproximações existentes entre a Modelagem e as Investigações Temáticas.
Para tanto, trago algumas questões acerca da Modelagem, assim como das Investigações
Temáticas.
No que diz respeito à metodologia, a pesquisa que deu origem a esse texto é
pautada no paradigma qualitativo, pois busca compreender as possíveis convergências
entre as Investigações Temáticas e a Modelagem no cenário nacional. Assim, ela foi
baseada em um estudo bibliográfico, podendo ser classificada então como uma pesquisa
bibliográfica (FIORENTINI; LORENZATO, 2006), ou seja, aquela que acontece
prioritariamente a partir de textos escritos.
As obras utilizadas foram basicamente aquelas que tratam da EMC, com ênfase
nas suas convergências com a Modelagem, as que apresentam a Modelagem na
perspectiva sociocrítica e também a produção de Paulo Freire como livros e artigos que
abordam as Investigações Temáticas.
A busca pelos textos que baseiam essa pesquisa foi realizada a partir das
publicações brasileiras em anais de eventos como os dois últimos SIPEM4 – Seminário
Internacional de pesquisa em Educação Matemática, as duas últimas CNMEM 5 –
Conferência Nacional de Modelagem na Educação Matemática, no Banco de Teses da
4
5
Realizados em Águas de Lindóia, SP, e, 2006 e em Brasília, DF, em 2009.
Realizadas em Londrina, PR em 2009 e em Belém, PA em 2011.
4
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
CAPES6, por meio de buscas virtuais com combinações de palavras-chaves e também
em consultas à bibliotecas e acervos (pessoais e de outros pesquisadores da área).
2
Modelagem Matemática e Educação Matemática Crítica
A Modelagem permeia o cenário da Educação Matemática há algum tempo,
conforme foi mencionado. Recentemente, ela passou a integrar também os documentos
oficiais do Ministério da Educação (MEC) como um caminho possível para os
processos de ensino e de aprendizagem da Matemática na Educação Básica (BRASIL,
2006). Na literatura específica sobre o tema, não há uma única definição de Modelagem,
mas as concepções apresentadas apontam convergências.
Desse modo, ela pode ser compreendida como um caminho para o “fazer”
Matemática em sala de aula. A partir de observações da realidade (do aluno e/ou do
mundo) e partindo de questionamentos, discussões e investigações, os estudantes, ao
fazerem Modelagem, defrontam-se com problemas que podem modificar as ações na
sala de aula, além da forma como se compreende o mundo (MEYER; CALDEIRA;
MALHEIROS, 2011). Tal ideia se aproxima daquilo que Freire (2005) denomina
“Leitura de Mundo”. Nesse texto, a Modelagem é vista como uma abordagem
pedagógica na qual os estudantes, a partir de um tema de interesse deles, utilizam a
matemática para investigá-lo e compreendê-lo, sendo o professor o orientador ao longo
de todo o processo.
Existem pequenas sutilezas que fazem com que as concepções de Modelagem
adotadas por pesquisadores apresentem aspectos diferenciados. No cenário educacional,
ela pode ser compreendida como um método de investigação e ser relacionada com a
ideia da integração da Matemática com outras áreas do conhecimento. É possível
encontrar uma revisão de literatura sobre as diferentes concepções de Modelagem em
várias publicações da área (MALHEIROS, 2004; ARAÚJO, 2002). Dando continuidade
às sutilezas que fazem a diferença nas perspectivas sobre Modelagem, alguns
pesquisadores acreditam que é possível trabalhar com qualquer tema ao se desenvolver
um trabalho com Modelagem e outros, não.
Além disso, a Modelagem é vista por muitos como uma estratégia pedagógica
motivadora, capaz de despertar o interesse do aluno pela Matemática, relacionando-a
6
Coordenação de Aperfeiçoamento Pessoal de Nível Superior. <http://www.capes.gov.br/servicos/bancode-teses>. Acesso em 15 nov. 2011.
5
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
com fatos do seu cotidiano ou, de modo mais incisivo, com as necessidades cotidianas
de suas comunidades. Com a Modelagem também pode-se criar possibilidades
interdisciplinares na sala de aula, fato considerado muito importante dentre as questões
relacionadas ao ensino e a aprendizagem, mostrando que, no caso, a Matemática não é
uma ciência isolada das outras.
Nesse sentido, autores como Bassanezi (2002) acreditam que quando a
aprendizagem é realizada por meio da Modelagem, os estudantes conseguem relacionar
a Matemática com suas aplicações, vislumbrando alternativas que possam direcionar
suas aptidões ou até sua formação.
Assim, em contraste com a ideia de alguns pesquisadores, a Modelagem também
pode ser vista como o esforço de descrever matematicamente um fenômeno que é
escolhido pelos alunos com o auxílio do professor. Com isso, o professor tem o papel de
conduzir seus alunos na transformação e matematização de um tema amplo em uma
questão mais restrita a ser investigada. E, a partir da matematização do tema escolhido
pelo aluno, este, muitas vezes, consegue compreender determinados fenômenos e
elaborar algumas conjecturas. Porém, o objetivo ao se trabalhar com Modelagem é, na
maioria das vezes, tentar compreender fatos, elaborar e atribuir significados aos
modelos, utilizando para isso a Matemática.
Desse modo, na Modelagem, o professor é um agente participante de todo o
processo, que busca auxiliar e orientar os alunos, com o objetivo de torná-los
protagonistas da produção do conhecimento. Assim, no trabalho com a Modelagem em
sala de aula, o docente deve estar preparado para possíveis imprevistos, principalmente
quando são os alunos que propõem o tema a ser desenvolvido.
Na literatura nacional, há perspectivas de Modelagem que se apoiam
principalmente nos conceitos da EMC, como os trabalhos de Araújo (2002; 2009), por
exemplo. Sobre tal temática, Jacobini e Wodewotzki (2006) publicaram um texto que
apresenta uma reflexão sobre a Modelagem no contexto da EMC e Araújo (2009) teceu
considerações sobre o que seria a Modelagem na perspectiva da EMC.
A EMC surgiu, no contexto da Educação Matemática, na década de 1980, a partir
da preocupação de educadores com os aspectos políticos da Educação Matemática, e
suas discussões giram em torno da questão da democracia (SKOVSMOSE, 2001). Nesta
perspectiva, o diálogo e a democracia devem estar presentes na sala de aula ao se fazer
matemática. Para Skovsmose (2008), a noção de diálogo proposta por Freire é uma das
6
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
inspirações teóricas para a educação crítica. Assim, na EMC, os estudantes possuem um
grau de envolvimento muito grande no desenvolvimento e controle do processo
educacional e, com isso, a relação existente entre o professor e os alunos tem papel
fundamental. “Vários tipos de relação são possíveis, mas a Educação Crítica enfatiza
que um princípio importante é que os parceiros sejam iguais” (SKOVSMOSE, 2001,
p.17). Sobre tal fato, Freire (2011a, p. 25) afirma que “[...] embora diferentes entre si,
quem forma se forma e re-forma ao formar e quem é formado forma-se e forma ao ser
formado”.
Para Skovsmose (2001), um dos pontos chave da EMC não está inserido no
processo educacional, mas está relacionado com problemas existentes fora do universo
da Educação. Assim, ele acredita que as questões estudadas devem ser relevantes para
os alunos, de acordo com seus interesses, além desses possuírem uma relação próxima
com situações ou problemas existentes em seu contexto social. Nesse sentido, afirma
que “a educação crítica deve ser baseada em diálogos e discussões, o que talvez seja
uma forma de fazer com que a aprendizagem seja conduzida pelos interesses dos
alunos” (SKOVSMOSE, 2008, p. 10). O autor ainda complementa que, “[...] para ser
crítica, a educação deve reagir às contradições sociais” (SKOVSMOSE, 2008, p.101) e
destaca que a EMC tem se manifestado por meio de orientações para problemas,
organização de projetos, interdisciplinaridade, dentre outros. A proposta da EMC é fazer
com que todos sejam matematicamente alfabetizados, para que eles possam vivenciar,
entender e questionar a sociedade em que vivem.
Ainda, em Alrø e Skovsmose (2006), os autores enfatizam que a EMC se
preocupa com a maneira com que a Matemática influencia o ambiente cultural,
tecnológico e político e acreditam que as competências matemáticas devem servir para
que isso aconteça. Desse modo, a EMC não está apenas preocupada com maneiras
“mais eficientes” de ensinar determinados conteúdos e sim com questões como “De que
maneira a aprendizagem da Matemática pode contribuir para o desenvolvimento da
cidadania?”, dentre outras. E, para eles, a comunicação, com base no diálogo, favorece
certas qualidades da aprendizagem de Matemática, “[...] a que nós nos referimos como
aprendizagem crítica da matemática manifestada na competência da materacia” (ALRØ;
SKOVSMOSE, 2006, p.19).
Considerando as questões apresentadas, acredito que ao se propor um trabalho
com Modelagem em sala de aula, com base em situações de interesse dos alunos e que
7
8
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
fazem parte do seu dia-a-dia, está se possibilitando ao estudante que ele compreenda o
papel da Matemática na sociedade. E tal fato vai ao encontro de
elementos da
perspectiva da EMC. A Modelagem, como aprendizagem da vida, como forma de ler o
mundo, como forma de compreendê-lo e de poder tomar decisões, converge para os
pressupostos apresentados por Skovsmose (2001; 2007) e outros autores antes aqui
mencionados.
Ademais, quando se trabalha com a Modelagem na perspectiva da EMC,
professores e alunos são participantes do processo de aprendizagem, não apenas da
Matemática, mas de questões relacionadas ao cotidiano e que possuam relevância
social, à cidadania e ao seu exercício consciente, além de questões relacionadas aos
interesses dos estudantes. Um aspecto que aproxima a Modelagem da EMC é o fato de
que, muitas vezes, não há uma única resposta ao problema investigado, ou então
existem muitos caminhos para que se chegue até ela. Tal fato permite que a Matemática
possa ser vista como uma área que possui influência humana, que pode ser questionada
(BORBA; SKOVSMOSE, 2001). Tal visão vai contra a ideologia da certeza da
Matemática, que para Borba e Skovsmose (2001), reforça a ideia de a Matemática se
tornar parte de uma linguagem de poder, ou seja, o argumento matemático não é contraargumentado, visto que ele é estável e inquestionável. Assim, a EMC tem como um de
seus objetivos combater a ideologia da certeza da Matemática e a Modelagem pode ser
um caminho para que isso aconteça.
E, sobre a Matemática, em particular, Skovsmose (2007) afirma que ela representa
uma preocupação da EMC, pois ela não deve ser considerada apenas de uma perspectiva
educacional, mas também de um ponto de vista filosófico e sociológico.
Assim como na Modelagem, o objetivo da EMC não é apenas que o indivíduo
aprenda Matemática e, sim, que ele a utilize para compreender seu entorno, sua
realidade e que possa, a partir dela, exercer sua cidadania. Nesse sentido, uma pesquisa
realizada com base nas premissas da EMC se compromete com transformações dos
sujeitos envolvidos, uma das bases do paradigma crítico, e vai ao encontro de ideias
presentes na obra freireana.
3
Investigação Temática
De acordo com Nascimento e Linsingen (2006), a problematização e a
dialogicidade são os dois princípios centrais que norteiam a filosofia de Paulo Freire. E,
para Freire (2005), problematizar ultrapassa a ideia de que, a partir de um problema ou
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
situação do cotidiano do estudante, o professor trabalhe certo conteúdo. Para ele,
problematizar é “[...] exercer uma análise crítica sobre a realidade problema” (FREIRE,
2005, p. 193), ou seja, é mais do que aprender um conteúdo ou conjunto deles e sim
compreender a situação em que este se mostra presente. Nessa direção, Nascimento e
Linsingen (2006, p. 104) destacam que “a problematização deve ser um processo no
qual o educando se confronta com situações de sua vida diária, desestabilizando seu
conhecimento anterior e criando uma lacuna que o faz sentir falta daquilo que ele não
sabe”. Tal concepção vai ao encontro da ideia de educação realizada com a participação
dos estudantes e não sobre eles, essa última baseada na concepção de uma “educação
bancária”, antidialógica (FREIRE, 2005).
E, para que a problematização seja incorporada ao contexto educacional, Freire
(2005) propõe o trabalho de conteúdos programáticos da educação a partir da
investigação de temas geradores, denominada por ele de Investigação Temática (IT),
considerada como ponto de partida do processo educativo. Segundo ele, tal “[...]
investigação implica, necessariamente, uma metodologia que não pode contradizer a
dialogicidade da educação libertadora” (FREIRE, 2005, p. 101), educação essa pautada
na ideia de que professor e alunos aprendem e ensinam juntos, por meio do diálogo.
Para Freire (2005), a educação libertadora, problematizadora, é aquela que supera a
contradição educador-educandos, ou seja, para ele, a educação é uma atividade na qual
os envolvidos, educandos e educadores, apesar da diferença que os conotam e
mediatizados pelo mundo, se educam em comunhão. Além disso, tal educação não
acontece de forma mecânica e, sim, por meio de investigação e reflexão, para o
desenvolvimento da criticidade, pois para Freire (2005), conhecer implica em interferir
na realidade conhecida.
Especificamente sobre a IT, Freire (2005) afirma que ela é realizada por meio de
uma metodologia conscientizadora, com o objetivo de proporcionar aos sujeitos uma
forma crítica de pensamento acerca das questões de seu cotidiano. Para ele, “investigar
o tema gerador é investigar [...] o pensar dos homens referido à realidade, é investigar
seu atuar sobre a realidade, que é sua práxis” (FREIRE, 2005, p. 114). Nesse contexto,
professor e alunos se tornam sujeitos do processo. Freire (2005) ainda ressalta que
quanto mais ativa for a postura dos indivíduos na investigação de uma temática, mais
eles se aprofundarão sobre ela e, então, se apropriarão dela.
A IT tem por objetivo explicitar o que Freire (2005) denomina de situações-
9
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
limites, as quais podem ser compreendidas como situações contraditórias ou barreiras
insuperáveis, mas que devem ser encaradas como um obstáculo à sua libertação,
possível de ser ultrapassado. Assim, a partir de tais situações devem emergir os temas
geradores, os quais guiarão as ações pedagógicas e permitirão aos educandos superar as
situações-limites. Com isso, os sujeitos deixam a realidade em que se encontravam e
passam a integrar outra, na qual assumem um posicionamento crítico. Nesse sentido,
“no momento em que a percepção crítica se instaura, na ação, se desenvolve um clima
de esperança e confiança que leva os homens a se empenharem na superação das
‘situações-limites’” (FREIRE, 2005, p. 105). Tal superação só acontece nas relações
entre homens-mundo, dialógicas, por meio de ações sobre a realidade.
Não obstante, a IT não pode ser reduzida a um ato mecânico, visto que consiste
em um processo de busca, de conhecimento, e, consequentemente, de criação. Assim,
exige dos sujeitos, a partir das descobertas, no encadeamento dos temas, a
interpenetração dos problemas, com o objetivo de compreender a totalidade que está
sendo investigada.
Já no processo de busca pelo tema, deve estar presente também a busca pela
problematização, considerando o vínculo com outros temas e também o seu papel e
envolvimento no contexto no qual está inserido. Para Freire (2005, p. 118) “[...] toda
investigação temática de caráter conscientizador se faz pedagógica e toda autêntica
educação se faz no exercício do pensar”. Assim, nesse modelo de educação, dialógica
por excelência, conforme afirma Freire (2005), os conteúdos não são “depositados” e
sim organizados e constituídos na visão de mundo dos educandos, mundo esse onde se
encontram os seus temas geradores. Com isso, espera-se que educandos e educadores
sejam capazes de realizar uma leitura crítica do mundo.
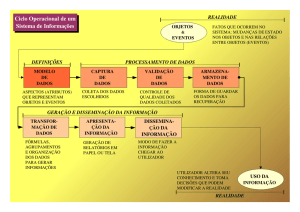
Para Freire (2005), a IT passa pelos processos de codificação, decodificação e
problematização, pois as contradições que os sujeitos vivenciam e observam são a eles
apresentadas como códigos que devem ser decodificados e problematizados para que a
superação dos mesmos seja possível, ou seja, eles devem problematizar as situações, até
então consideradas “situações-limites”.
Depois de delimitada a área na qual se vai trabalhar, a primeira etapa se inicia
com um diálogo com os indivíduos e observações, com intuito de realizar um
levantamento preliminar das condições do local. Nesses contextos são identificadas as
contradições, as “situações-limites”. Na sequência, são eleitas algumas dessas
10
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
contradições e, a partir delas, são preparadas as codificações que serão apresentadas aos
sujeitos na terceira etapa, para que eles possam analisar sua própria realidade. Freire
(2005, p. 130) denomina esses exercícios de “[...] diálogos decodificadores, nos
‘círculos de investigação temática’”.
Na etapa seguinte, tem início o estudo sistemático e interdisciplinar das
informações coletadas, para que então possa ser realizada a delimitação temática, por
cada um dos especialistas envolvidos no processo. Assim, será feita a redução temática.
Entretanto, nesse processo de redução dos temas, Freire (2005, p. 134) destaca que “[...]
a equipe reconhecerá a necessidade de colocar alguns temas fundamentais que, não
obstante, não foram sugeridos pelo povo, quando da sua investigação”. Ainda, o autor
reforça que a inclusão de tais temas corresponde à perspectiva dialógica da educação,
que permite que os educadores também participem dela, sugerindo temas que
consideram importantes. Na sequência, acontece a última etapa no contexto
educacional, a partir do material elaborado pela equipe, com base nos temas. E, para que
ela ocorra, Freire (2005) sugere, a partir de um exemplo, alguns procedimentos
didáticos, como debates, dramatizações, etc. e afirma que independente da metodologia
utilizada,
o importante, do ponto de vista de uma educação libertadora, e não
“bancária”, é que, em qualquer um dos casos, os homens se sintam
sujeitos do seu pensar, discutindo o seu pensar, sua própria visão do
mundo, manifestada implícita ou explicitamente, nas suas sugestões e
de seus companheiros (FREIRE, 2005, p. 139).
Nesse sentido, as ideias das Investigações Temáticas, propostas por Freire (2005),
apontam para o diálogo e a problematização de temas de interesse dos educandos como
um caminho para a aprendizagem crítica e reflexiva. E elas apresentam convergências
com algumas premissas da Modelagem, pautadas principalmente na abordagem
sociocrítica, conforme explicitarei na sequência.
4
Diálogos entre a Modelagem e a Investigação Temática
Conforme apresentado anteriormente, algumas concepções de Modelagem podem
ser classificadas de acordo com a perspectiva sociocrítica e são baseadas nas ideias da
EMC, pois ao se levar a Modelagem para sala de aula, com base em situações de
interesse dos alunos e que fazem parte do seu dia-a-dia, pode-se possibilitar ao
estudante a compreensão do papel da Matemática na sociedade. Ao analisarmos as
publicações de Skovsmose acerca da EMC, Freire e sua perspectiva dialógica sempre
11
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
são mencionados, relacionado principalmente com a ideia de materacia, que não se
resume apenas às habilidades matemáticas, “mas também a competência de interpretar e
agir numa situação social e política estruturada pela matemática” (SKOVSMOSE, 2008,
p. 16).
Nas obras de Paulo Freire, sua ênfase é na alfabetização. Entretanto, em uma
entrevista sobre Educação Matemática, Freire evidencia a importância do conhecimento
matemático para a leitura do mundo. Segundo ele, “a vida que vira existência se
matematiza” e, com isso, enfatiza a necessidade de educadores e professores de
matemática desmistificarem a Matemática ensinada na escola. Para Freire, a
alfabetização matemática, que ele denominou de mate-alfabetização ou math-literacy,
contribuiria para o desenvolvimento da cidadania. Freire acredita que os professores
devem despertar os estudantes para que eles se assumam enquanto matemáticos e, para
que isso ocorra, o professor tem que ter consciência do que é ensinar.
Um outro saber que eu preciso saber é que ensinar não é transferir
conhecimento, transferir conteúdo. É lutar para com os alunos, criar
condições para que o conhecimento seja construído, seja reconstruído.
Isso para mim é ensinar. [...] É preciso que eu, como professor, saiba
que do ponto de vista histórico, o homem e a mulher primeiro
aprenderam, para depois ensinar. O aprender precedeu sempre o
ensinar. [...] Agora, é preciso clarear e esclarecer o que significa
mesmo ensinar. [...] eu produzo, eu crio, eu recrio o conhecimento, eu
não engulo conhecimento. [...] Conhecimento eu produzo socialmente
(FREIRE, 1996, <http://vello.sites.uol.com.br/entrevista.htm>. Acesso
em 10 de mai. 2012).
Nessa perspectiva, Santos (2007) evidencia que, para Freire, um educador não é
compreendido como uma figura estática e descomprometida com o seu quefazer e sim
um sujeito dialógico, crítico e preocupado com as questões sociais. O educador é aquele
que permite que o aluno participe do processo de construção de seu próprio
conhecimento e, para isso, deve lançar mão de metodologias em sinergia com tais
propósitos, que vão ao encontro das ideias de Modelagem e de EMC apresentadas até
então. Para Freire, uma dessas metodologias era a IT. No contexto da Educação
Matemática, acredito que a Modelagem pode ser considerada como uma dessas
metodologias. Para Forner (2005, p.49), a relação entre o pensamento freireano e a
Modelagem existe “[...] quando se parte de uma situação contextualizada, trabalha sobre
ela, estimula-se o diálogo para chegar a uma resolução, estabelecendo inclusive uma
discussão válida sobre os resultados apresentados”. Assim, possibilitar que os alunos
12
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
façam Modelagem é, possivelmente, permitir que eles se assumam enquanto
matemáticos, conforme destacou Freire.
Na direção do que afirma Forner (2005), é possível caracterizar a Modelagem
como uma IT, pois assim como nas Investigações Temáticas, na Modelagem a
problematização e o diálogo são fatores imprescindíveis. Ainda, ao se trabalhar com
Modelagem a partir de um tema de interesse dos estudantes, tanto professor quanto
alunos aprendem e ensinam, pois muitas vezes o educador precisa aprender sobre o
tema eleito para atuar enquanto mediador dos processos de ensino e de aprendizagem e,
além disso, mesmo que o tema não seja novo para o educador, enquanto o educador
ensina os educandos ele aprende saberes da prática docente.
E, assim como a IT não pode ser reduzida a um ato mecânico, o mesmo pode ser
afirmado acerca da Modelagem, pois nela se exige a busca, a problematização, a
investigação e a análise da(s) solução(ões) encontrada(s) no contexto da situação
problematizada.
Conforme afirma Freire (2005), a IT passa pelos processos de codificação,
decodificação e problematização. Tais processos podem ser encontrados também ao se
fazer Modelagem, na medida em que, primeiramente, se escolhe um tema para
investigar, em comunhão, pois, segundo ele “daí também que o conteúdo programático
para a ação, que é de ambos [educador e educando] não possa ser de exclusiva eleição
daqueles, mas deles e do povo” (ibidem, p. 101). A escolha do tema deve ser de algo
que tenha significado para os educandos, e “o conceito do ‘tema gerador’ não é uma
criação arbitrária, ou uma hipótese de trabalho que deva ser comprovada” (ibidem, p.
102) e sim algo que se queira compreender melhor em sua plenitude.
Na Modelagem, a codificação do tema pode ser entendida como a compreensão
do mesmo, a partir das informações que se tem a priori, informações essas que
suscitaram o interesse na investigação. A decodificação acontece quando se mergulha
no tema e o compreende numa esfera mais ampla. Para Freire (2005), a decodificação é
um ato cognoscente que pode promover o surgimento de uma nova percepção e, com
isso, a construção do conhecimento. A partir de então acontece a problematização, que
na Modelagem podemos entender como o processo de escolha do problema gerado a
partir do tema eleito. Desse momento em diante, a Matemática se torna uma das atrizes
na compreensão e/ou resolução de tal problema.
A ideia de situação-limite, proposta por Freire (2005), pode ser interpretada no
13
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
contexto da Modelagem quando são encontradas possíveis contradições ao se investigar
determinado problema, principalmente quando esse problema é real, faz parte da
comunidade em que se vive. Assim, é possível inferir que, por meio da Modelagem, os
educadores, partindo de uma educação problematizadora, podem debater questões de
cunho social, com a finalidade de desenvolver o pensamento crítico dos educandos, a
partir das situações-limites.
Desse modo, as ideias de Freire acerca das Investigações Temáticas convergem
para os pressupostos da Modelagem, pautada na EMC, principalmente quando o tema
eleito para o trabalho faz parte do cotidiano e da realidade dos estudantes.
5
Considerações Finais
Para Jacobini e Wodewotzki (2006), Paulo Freire foi o pioneiro no Brasil a
apresentar questionamentos acerca de posturas democráticas, com posicionamentos
críticos, com reflexões sobre a razão e a finalidade do ensino, em uma esfera mais
ampla. Tais ideias foram levadas para EMC, visto que Skovsmose referencia o
pensamento freireano em boa parte de suas obras. E, na Modelagem, há uma corrente
que se inspira nas premissas da EMC, conforme citado anteriormente. Diante desse
cenário, esse texto, de cunho teórico, teve como objetivo apresentar as ideias da obra
freireana, e, em particular, as convergências existentes entre a IT, proposta por Freire, e
a Modelagem, de uma perspectiva da EMC.
Por meio do estudo das Investigações Temáticas, encontrei convergências entre
elas e a Modelagem, na medida em que em ambas se busca, além da construção do
conhecimento, a reflexão e o despertar da consciência crítica do educando e dos
educadores.
Ademais, Freire (2005) destaca que nas Investigações Temáticas pode ocorrer o
que ele denomina de o tema do silêncio, quando o grupo de educandos não consegue
apresentar um tema de interesse para a investigação. Para ele, tal fato “sugere uma
estrutura constituinte do mutismo ante a força esmagadora de ‘situações-limites’, em
face das quais o óbvio é a adaptação” (ibidem, p. 114). Isso também acontece, em
alguns momentos, quando se propõe para uma turma escolher um tema de interesse
deles para o trabalho com Modelagem. Há muitas vezes a dificuldade da eleição de algo
que se quer investigar. Acredito que isso pode acontecer pela falta de hábito dos
estudantes em participar das decisões em sala de aula.
Para Freire (2005, p. 118), “toda investigação temática de caráter conscientizador
14
15
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
se faz pedagógica e toda autêntica educação se faz investigação do pensar”. Vejo que tal
afirmação vai ao encontro das ideias de Modelagem apresentadas nesse texto,
mostrando mais uma vez as convergências entre ela e as Investigações Temáticas.
Observo, entretanto, que, nesse texto, não esgotei as possíveis convergências entre
a obra de Paulo Freire e a Modelagem e, sim, apresentei uma pequena parte das
possíveis aproximações entre elas. Assim, fica aqui o registro para que novos estudos
sejam realizados, com vistas a contribuir para que a comunidade que investiga e
trabalha com Modelagem em sala de aula possa compreender as influências de Freire
nessa metodologia de ensino.
Agradecimentos
Embora não sejam responsáveis pelo conteúdo desse artigo, agradeço a Aparecida
Chiari, Debora Soares, Luana Oliveira, Rúbia Amaral e Silvana Santos pelas críticas e
sugestões em suas versões preliminares.
Referências
ALRØ, H.; SKOVSMOSE, O. Diálogo e Aprendizagem em Educação Matemática.
Tradução de FIGUEIREDO, O. Belo Horizonte: Autêntica, 2006.
ARAÚJO, J. L. Brazilian Research on Modelling in Mathematics Education. ZDM
Mathematics Education. 42:337–348. DOI 10.1007/s11858-010-0238-9. 2010.
ARAÚJO, J. L. Uma Abordagem Sócio-Crítica da Modelagem Matemática: a
perspectiva da educação matemática crítica. In: ALEXANDRIA - Revista de Educação
em Ciência e Tecnologia, v.2, n.2, p.55-68, jul. 2009.
ARAÚJO, J. L. Cálculo, Tecnologias e Modelagem Matemática: as discussões dos
alunos. 2002. Tese (Doutorado em Educação Matemática) - Instituto de Geociências e
Ciências Exatas (IGCE), Universidade Estadual Paulista (UNESP), Rio Claro - SP,
2002.
BARBOSA, J. C. Sobre a pesquisa em modelagem matemática no Brasil. In.
Conferência Nacional sobre Modelagem na Educação Matemática, 5 (V CNMEM).
Ouro
Preto,
MG.
Anais...
Ouro
Preto:
Universidade
Federal
de
Ouro
Preto/Universidade Federal de Minas Gerais. 2007. V. único.
BARBOSA, J. C. Modelagem Matemática e a Perspectiva Sócio-Crítica. In: Seminário
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
Internacional de Pesquisas em Educação Matemática, 2 (II SIPEM). 2003. Santos, SP.
Anais... São Paulo: Sociedade Brasileira de Educação Matemática, 2003. V. único.
BARBOSA, J. C. Modelagem Matemática: Concepções e Experiências de Futuros
Professores. 2001. Tese (Doutorado em Educação Matemática) - Instituto de
Geociências e Ciências Exatas (IGCE), Universidade Estadual Paulista (UNESP), Rio
Claro - SP, 2001.
BASSANEZI, R. C. Ensino-aprendizagem com Modelagem Matemática: uma nova
estratégia. Editora Contexto: São Paulo, 2002.
BIEMBENGUT, M. S. 30 Anos de Modelagem Matemática na Educação Brasileira: das
propostas primeiras às propostas atuais. ALEXANDRIA: Revista de Educação em
Ciência e Tecnologia, v.2, n.2, p.7-32, jul. 2009.
BORBA, M. C.; VILLARREAL, M. E. Humans-with-Media and the Reorganization
of Mathematical Thinking: Information and Communication Technologies, Modeling,
Visualization and Experimentation. New York: Springer Science+Business Media, Inc.,
2005.
BORBA, M. C.; SKOVSMOSE, O. A Ideologia da Certeza em Educação Matemática.
In. Educação Matemática Crítica : A Questão da Democracia. Campinas: Papirus, p.
127 – 160. 2001.
BRASIL. Secretaria de Educação Média e Tecnológica. Orientações Curriculares
para o Ensino Médio. V. 2. Ciências da Natureza, Matemática e suas Tecnologias.
Brasília: Ministério da Educação, 2006.
FIORENTINI, D.; LORENZATO, S. Investigação em Educação Matemática:
percursos teóricos e metodológicos. Campinas, SP: Autores Associados, 2006.
FORNER, R. Paulo Freire e Educação Matemática: reflexões sobre a formação do
professor. 2005. Dissertação (Mestrado em Educação) – Centro de Ciências Sociais e
Aplicadas, Pontifícia Universidade Católica de Campinas (PUCCamp), Campinas - SP,
2005.
FRANCHI, R. H. O. L. Uma proposta curricular para cursos de Engenharia
utilizando Modelagem Matemática e Informática. 2002. Tese (Doutorado em
Educação Matemática) - Instituto de Geociências e Ciências Exatas, Universidade
Estadual Paulista, Rio Claro, 2002.
16
17
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
FREIRE, P. Pedagogia da Autonomia: saberes necessários à prática educativa. São
Paulo: Paz e Terra, 2011a.
FREIRE, P. Educação como prática de Liberdade. 14ª Edição. Versão atualizada. Rio
de Janeiro: Paz e Terra, 2011b.
FREIRE, P. Pedagogia do Oprimido. 49ª Reimpressão. Rio de Janeiro: Paz e Terra,
2005.
FREIRE,
P.
D’Ambrosio
entrevista
Paulo
Freire.
1996.
Disponível em
<http://vello.sites.uol.com.br/entrevista.htm>. Acesso em 10 de Ago. 2011.
FREIRE, P. A importância do ato de ler: em três artigos que se completam. 23ª
edição. São Paulo: Autores Associados: Cortez, 1989.
JACOBINI, O. R., WODEWOTZKI, M. L. L. Uma Reflexão sobre a Modelagem
Matemática no contexto da Educação Matemática Crítica. In: Bolema – Boletim de
Educação Matemática. Ano 19, nº 25, 2006. pp. 71 a 88.
MALHEIROS, A. P. S. Pesquisas em Modelagem Matemática e diferentes tendências
em Educação e em Educação Matemática. : Bolema – Boletim de Educação
Matemática. 2012. No prelo.
MALHEIROS, A. P. S. Educação Matemática online: a elaboração de projetos de
Modelagem Matemática. 2008. Tese (Doutorado em Educação Matemática) - Instituto
de Geociências e Ciências Exatas (IGCE), Universidade Estadual Paulista (UNESP),
Rio Claro - SP, 2008.
MALHEIROS, A. P. S. A Produção Matemática dos Alunos em Ambiente de
Modelagem Matemática. 2004. Dissertação (Mestrado em Educação Matemática). Instituto de Geociências e Ciências Exatas (IGCE), Universidade Estadual Paulista
(UNESP), Rio Claro - SP, 2004.
MEYER, J. F. C. A.; CALDEIRA, A. D.; MALHEIROS, A. P. S. Modelagem em
Educação Matemática. Belo Horizonte, MG: Autêntica Editora, 2011.
NASCIMENTO, T. G.; LINSINGEN, I. Articulações entre o enfoque CTS e a
Pedagogia de Paulo Freire como base para o Ensino de Ciências. In: Convergencia –
Universidade Autónoma Del Estado de México. Ano/vol. 13, n° 42, p. 95-116,
setembro-dezembro, 2006.
V SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA
28 a 31 de outubro de 2012, Petrópolis, Rio de Janeiro, Brasil
SILVA, D. S. Educação Matemática Crítica e a Perspectiva Dialógica de Freire: tecendo
caminhos para a formação de professores. In: ARAÚJO, J. L.(Org.) Educação
Matemática Crítica: reflexões e diálogos. Belo Horizonte, MG: Argvmentvm, 2007.
SKOVSMOSE, O. Educação Crítica: incerteza, matemática, responsabilidade.
Tradução de BICUDO, M. A. V. São Paulo: Cortez, 2007.
SKOVSMOSE, O. Educação Matemática Crítica: a questão da democracia.
Campinas, SP: Papirus, 2001.
18